基于手机信令数据的服务业网点空间布局与人口耦合关系研究

期刊菜单

基于手机信令数据的服务业网点空间布局与人口耦合关系研究
Study on Coupling Relationship between Spatial Layout of Service Outlets and Population Based on Mobile Signaling Data in Zhongshan

DOI:10.12677/HJDM.2020.104024,PDF,HTML,XML,下载: 737浏览: 1,204科研立项经费支持
作者:陈佳懿,肖莉^*,潘怡颖,华海静：华南农业大学数学与信息学院，广东广州
关键词:手机信令数据；POI数据；动态聚类；异常分析；中山市；Mobile Phone Signaling Data；POI Data；Dynamic Clustering；Anomaly Analysis；Zhongshan

摘要:服务业空间的合理布局是推动城市经济发展、满足居民消费需求的基础，服务业空间与人口的耦合度高低是衡量服务业布局优劣的重要依据。手机信令数据和城市兴趣点(POI)数据能够很好地反映城市人口分布和城市热点分布。本文以中山市为研究对象，利用2018年手机信令数据与POI数据，探究并分析了该市服务业网点的空间布局特征，并提出了基于动态聚类的手机信令数据人口耦合度模型，通过异常分析判断地区人口耦合情况优劣，并根据分析结果提出建议。

Abstract:Reasonable distribution of service industry is the basis to promote urban economic development and meet the consumption demand of residents. The coupling degree of service industry space and population is an important basis to measure the advantages and disadvantages of service industry layout. Mobile phone signaling data and POI data can well reflect the distribution of urban popula-tion and urban hot spots. This paper takes Zhongshan as the research object, using the mobile phone signaling data and POI data in 2018, explores and analyzes the spatial layout characteristics of the city's service industry outlets, puts forward the population coupling model of mobile phone signaling data based on dynamic clustering, judges the advantages and disadvantages of regional population coupling through abnormal analysis, and puts forward suggestions according to the analysis results.

文章引用：陈佳懿, 肖莉, 潘怡颖, 华海静. 基于手机信令数据的服务业网点空间布局与人口耦合关系研究[J]. 数据挖掘, 2020, 10(4): 229-239. https://doi.org/10.12677/HJDM.2020.104024

1. 引言

服务业的发展是满足居民消费需求、推动城市化进程的基础，服务业空间与人口的耦合度高低是衡量服务业布局优劣的重要依据。近年来，利用手机信令数据的时空动态性为挖掘人口空间分布特征提供了新的角度，能够更准确地为城市规划提出建议 [1] [2] [3]。另外，随着POI数据的获取、更新技术进步，其包含的地理位置信息愈发准确，越来越多的研究视角聚焦于POI在城市空间布局方面的应用 [4] [5] [6]。彭 [7] 基于手机信令数据与POI数据，提出了挖掘与判别城市的热点区域的方法，体现了两类数据在空间分析的相容性。钮 [8] 提出了利用手机信令数据识别城市空间结构的方法，能够识别手机用户的就业、居住、游憩等空间。张 [9] 以上海市零售商业POI数据和人口数据为基础，分析了上海市零售业空间布局特征与人口耦合关系，但未对地区人口耦合情况差异进行比较。

综上，目前国内对于服务业空间布局的研究方法和理论十分丰富，且对新型数据的使用有广泛的研究。但是针对人口耦合情况，仍拘泥于图像和数值的表象性，欠缺通过科学的统计对地区的人口耦合情况进行差异性分析，分析效率低、人工分析成本大，不利于空间研究的推进与发展。

2. 研究区域、数据来源和研究方法

2.1. 研究区域

中山，广东省地级市，下辖18个镇，6个街道，位于珠江三角洲中部偏南的下游出海处，为珠三角中心城市之一。作为粤港澳大湾区重要节点城市，对周边省市具有极强的辐射能力。近10年来，中山市的第三产业(服务业)占生产总值构成比例逐年上升，并有超越第二产业成为中山市生产总值的第一来源的趋势。可见，研究中山市的服务业的空间分布与人口耦合关系对中山市的城市化发展有重要意义 [10]。

2.2. 研究数据

2.2.1. 手机信令数据

本文的数据源是中山市所有手机用户于2018年11月生成的手机信令数据。经统计，数据源中共包含3,113,091名手机用户的移动轨迹数据，基本能表征出中山市所有居民的行为特征。经过大数据平台进行初步筛选和统计得到本文所采用的数据，现选取数据源中部分轨迹数据如表1进行展示。

Table 1. Mobile signaling data example

表1. 手机信令数据示例

移动通讯网络是由一系列的蜂窝基站构成的，这些蜂窝基站把整个通信区域划分成若干蜂窝小区。手机运行时，附近的移动通讯网络会标记用户所在基站覆盖的蜂窝小区，由此产生手机信令数据。利用该特点，本文将时间阈值位于22:00~8:00内停留超过4小时的信令基站位置判断为“居住点”，得到居住口径数共11,604条。

通过居住口径与统计年鉴常住人口数的占比进行配对t检验，可以得知在0.05的显著性水平下，由手机信令数据得到的居住口径实际情况之间不具备显著差异性，证明了由手机信令数据得到的居住口径对应的各镇(区)人口占比的准确性，采用居住口径得到的人口比例进行地区的服务业网点的人口耦合度计算是可行的。

2.2.2. POI数据

POI (Point of Interest)，即兴趣点，本文的数据来源为百度地图开发的API，由于现代服务业分类体系并无明确规定，本研究筛选分类依据为《国民经济行业分类》对现代服务业的详细解释与描述，以及百度地图POI分类体系的各类别描述。

本研究数据来源为2019年6月从百度地图获取的POI数据，通过纠偏和矫正，筛选提取出研究区域的服务业点信息共43,625条，并通过电话询问等方法确定数据的准确性，把服务业分为4种业态类型(大类)和10种网点类型(小类)，如下表2所示。

Table 2. POI data of Zhongshan

表2. 中山市POI数据

2.3. 基于手机信令数据的人口耦合模型

2.3.1. 基于动态聚类法的耦合度模型

1) 动态聚类法

动态聚类法是一种使用于大样本的Q型聚类分析方法，其基本思想是先粗略地进行预分类，然后通过某种最优准则进行逐步调整，直至将类别分得比较合理为止。

2) K-Means聚类

K-Means算法是最具有代表性基于距离的聚类算法，通常以误差平方和最小作为判断标准进行分类，如公式(1)所示，将n个样本x划分为k个互不相交的聚类簇Z，其中 $μ_{j}$ 为簇的中心。

$\sum_{i = 0}^{n} \sum_{j = 0}^{k} \min_{μ_{j} \in Z_{j}} (‖ x_{i} - μ_{j} ‖)$ (1)

本文共有两部分使用K-Means聚类算法：耦合度计算与耦合情况类型分类。其聚类方式可由如下流程图所示(图1)：

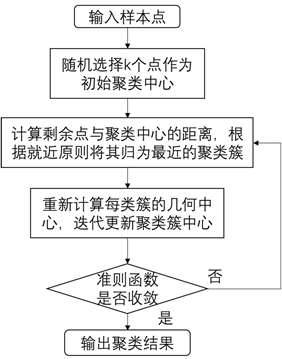
Figure 1. Flow chart of K-means clustering

图1. K-Means聚类法流程图

本文在耦合度计算过程，由于手机信令判断得到的居住点需要划定区域确定被服务范围，有别于通过街道信息划定区域，以距离作为衡量网点的服务区域更能够反映实际情况。在本文耦合度的计算中，利用动态聚类法将各区(镇)居住点按距离分为K簇，每簇定义为一个“居住聚集区”，认为该区域内的居民具有一致的被服务区域，用于居住点与服务网点的耦合度C计算。

3) 人口耦合度模型的构建

本文对手机信令得到的居住点人口规模与POI服务业网点的耦合情况进行分析，首先定义人口与各服务网点耦合度C，模型如下：

${\begin{cases} c q_{i} = \sum_{k = 1}^{K} \sum_{j = 1}^{n_{k}} c q_{i j} = \sum_{k = 1}^{K} \sum_{j = 1}^{n_{k}} \frac{P_{j}}{P q_{k}} \times \frac{m a x d_{i}}{d_{i j}} \\ C_{i} = \sum_{k = 1}^{m} \frac{n_{q}}{N} \times c q_{i} \end{cases}$ (2)

式中， $c q_{i}$ 为q镇(区)在i服务业网点类型的耦合度； $P_{j}$ 为居住点的人数， $P q_{k}$ 为q镇(区)中居住聚集区最大人口居住点的人数； $d_{i j}$ 为对应住宅点的邻近值， $m a x d_{i}$ 为i服务业网点在区域内最大的邻近值。 $C_{i}$ 为中山市在i服务业网点的耦合度，等于对应网点的各镇(区)耦合度人口加权平均。

在此基础上，定义人口与各业态类型耦合度Q，模型如下：

${\begin{cases} Q q_{i} = \sum_{i = 1}^{m_{P}} w_{i} c q_{i} \\ Q_{i} = \sum_{k = 1}^{m} \frac{n_{q}}{N} \times Q q_{i} \end{cases}$ (3)

其中， $m_{P}$ 为大类包含的小类数量， $w_{i}$ 是大类服务类型对应的第i小类权重，权重计算为：

$w_{i} = \frac{第 i 小类网点数量}{大类中所有网点总数量}$ (4)

2.3.2. 空间点模式分析

1) 最邻近指数(Nearest Neighbor Index, NNI)

NNI测度方法用于研究其服务业空间的分布模式，分析各个服务业空间实体在区域空间中的邻近程度，探索各类服务业空间的集聚与分散程度，具体方法如下：

$I_{N N} = \frac{d_{N N}}{d_{r a n}} = \sum_{i = 1}^{n} \frac{\min (d_{i j})}{n} \times \frac{1}{d_{r a n}}$ (5)

在本文， $I_{N N}$ 为居住口径与各类服务业网点的最邻近距离系数，n为服务业网点样本数目， $d_{i j}$ 为服务网点i到居住点j的距离， $\min (d_{i j})$ 为服务网点i到最邻近居住点的距离， $d_{m n}$ 为服务业网点空间随机分布条件下的平均距离，取 $d_{r a n} = 0.5 \sqrt{\frac{A}{n}}$ ，其中A为中山市面积。

$I_{N N}$ 大于1时，该类中山市服务网点格局聚集，最邻近点对间平均距离会小于平均随机距离；否则，该类中山市服务网点格局分散分布，最邻近点对间平均距离大于平均随机距离。且 $I_{N N}$ 比值越小，该类中山市服务网点集聚；比值越大，该类中山市服务网点格局越分散。同时，采用Z值检验计算结果的统计显著性，公式如下：

$Z = \frac{d_{N N} - d_{r a n}}{S E_{d_{r a n}}}$ ， $S E_{d_{r a n}} = \sqrt{\frac{(4 - π) A}{4 π n^{2}}}$ (6)

式中，SE为Z的标准误差。在0.01的置信度下，Z值小于−2.58，该服务业网点模式属于集聚模式；若Z值大于2.58，则该服务业网点模式属于均匀模式。

2) 空间核密度估计法

按照单位范围内的信息数据来估算其布局密度。研究区域中山市的空间区为s处的核密度计算函数为：

$f (s) = \sum_{i = 1}^{n} \frac{1}{h^{2}} k (\frac{c_{s} - c_{i}}{h})$ (7)

式中，n是与位置s的距离小于或等于h的服务网点数目；h是距离衰减阈值；k函数则表示空间权重函数，这一函数是指研究对象的密度值在每个核心要素处最大，并且核密度值随着距离的增大而降低，直至与核心的距离达到阈值h时研究对象的核密度值降为0。

3) Ripley’s K函数聚类分析

是一种对数据点进行不同距离的聚类程度的点数据模式分析方法，表明点要素核心空间的聚集或离散程度，以及在研究区域大小发生变化时是如何变化的。计算公式为：

$K (r) = A \sum_{i}^{n} \sum_{j}^{n} \frac{w_{i j} (r)}{n^{2}}$ ， $L (r) = \sqrt{\frac{K (r)}{π}} - r$ (8)

式中，r为既定或计算得到的距离阈值；A为中山市面积；n为各类服务业网点的样本点数目； $w_{i j} (r)$ 表示在距离r范围内，某一类中服务业网点i与网点j之间的距离， $L (r)$ 函数是 $K (r)$ 作开方的线性变换。

$L (r)$ 与r的关系可以检验在距离r范围内，各类服务业的空间分布格局。如果 $L (r)$ 大于预期值，即 $L (r) > 0$ ，表示该类服务业呈集聚分布；如果 $L (r)$ 小于预期值，即 $L (r) < 0$ ，则表示该类服务业成分散分布；若 $L (r) = 0$ ，说明该类服务业随机分布。

3. 模型结果与分析

3.1. 基于NNI的服务业网点空间布局模式

对所采集的中山市服务业网点数据进行最邻近距离分析后，结果如表3所示。

Table 3. Statistical results of nearest neighbor distance analysis

表3. 最邻近距离分析统计结果

从表3可以看出，中山市各类服务业网点的值均小于1，Z值均小于−2.58，故在0.01的置信水平下，各类网点的空间模式均呈现显著聚集分布，可以确定中山市内的服务业网点与居住点显著聚集。其中，与居住点集聚程度最强的为行政机构， $I_{N N} = 0.250$ ；其次为特色商业街、家居建材、美食；较为分散的是，酒店、生活服务、超市、商店、运动健身和旅游景点，其中旅游景点最为分散， $I_{N N} = 0.444$ 。

3.2. 基于核密度估计的集聚热点分析

服务业高度集中的地区是城市整体空间的重要位点，因此需要利用空间核密度估计法分析各类服务业网点的空间布局密度，以探索服务业空间集聚热点区域。本文基于中山市10种网点的POI数据，在单位范围内对43,625个服务业网点周边的点布局密度进行估算。利用自然间断点分级法设置阈值，可以得到10种服务业网点的空间聚集热点分布如图2。

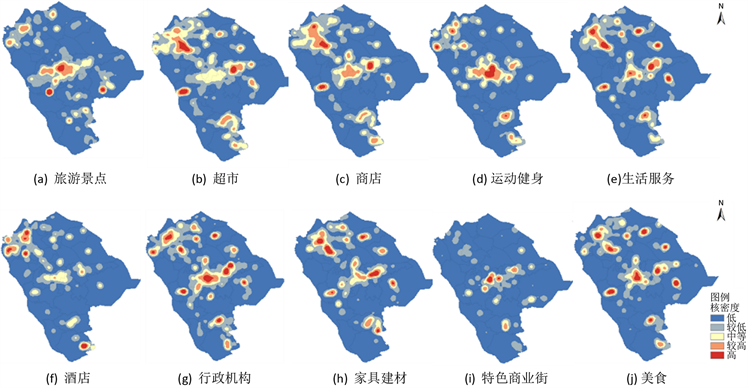
Figure 2. Spatial kernel density analysis of 10 kinds of outlets in Zhongshan

图2. 中山市10类网点空间核密度分析

图2的(a)表明：中山市的旅游景点主要集聚于南朗镇、南区街道与石岐区街道，孙中山故里与中山影视城位于南朗镇，为中山市旅游景点之首；坐落于南区北台的中山詹园，是目前岭南最大的私家庭院；而孙文西路步行街与中山公园，位于石岐闹市中心，同样能够吸引大量游客。

图2的(b)、(c)和(e)表明：中山市的超市、商店与生活服务的聚集区主要为大涌镇、东升镇和火炬开发区街道，并且相对均匀地分布在各大中心。

图2(d)代表的运动健身与(i)代表的特色商业街则主要沿内环集聚于石岐区街道；(g)代表的行政机构、(h)代表的家居建材市场与(j)代表的美食广泛分散地分布于市域范围内；(f)代表的酒店则零散地聚集在外环。

因此，综合分析图2可知，中山市服务业各类网点空间布局不均衡，集中在人口密集的镇区：超市、商场相对均匀地分布于市内，城市中心分布特色商业街、运动健身、美食区等居民日常生活需求类服务，而城市边缘则分布着家居建材市场、酒店等消费目的性较强的服务业空间。

3.3. 基于Ripley’s K函数的空间聚类分析

由于同样的服务业网点分布数据的聚类特征会随聚类距离选择的改变而变化，利用Ripley’s K函数计算观测K值，判断在各类网点在不同距离上的聚类程度变化。为了便于直接观察观测值和预期值的差距，本文利用公式8，进一步计算各类服务业网点在不同距离上的L(r)值，以分析中山市各类服务业网点的空间聚类模式，得到结果如图3所示。

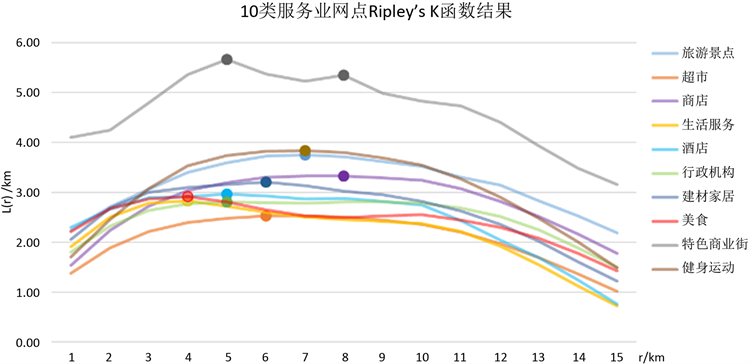
Figure 3. Results of Ripley’s K function for 10 service outlets

图3. 10类服务业网点Ripley’s K函数结果

由图3可知，在1~15 km的距离空间范围内，中山市的各类服务业空间集聚特征比较一致。L(r)曲线中特色商业街呈现明显“波浪型”，其余均呈现“倒U型”，表示各类空间在此距离范围内基本呈现先聚集再分散的空间特征，而特色商业街的分散程度较低，集中聚集在特定区域。从峰值出现的距离看，所有的服务业网点峰值均出现在4~8 km的范围内，分布尺度相对较小，其中生活服务与美食的峰值出现在4 km附近，分布尺度最小。

综上所述，中山市服务业各类网点呈现出在相对较小的距离选择区位聚集的布局状态。

3.4. 中山市服务业人口耦合分析

人口规模是影响服务业空间格局的主要因素，为从人口规模角度分析服务业空间规模和选址布局的合理性，本文建立服务业人口耦合模型计算各类业态类型和网点人口耦合度，以进一步分析中山市人口分布聚集程度与服务业网点的耦合适宜程度。

通过公式(2)计算得到各居住点耦合度，利用自然间断点分级法并通过人为调整将耦合度分为四个等级(差、中、良、优)，以判定中山市内各镇(区)居住口径的耦合情况优劣。给出耦合等级划分如表4。

Table 4. Coupling degree classification

表4. 耦合度等级划分

3.4.1. 服务业人口耦合度分析

以业态类型的耦合度为切入点进行分析，得到结果如表5所示。

Table 5. Coupling degree of four business types

表5. 四种业态类型耦合度

由耦合度可以看出中山市的人口与服务业网点呈现的耦合趋势为：

公共服务类(Q2，优) > 综合购物类(Q4，良) > 餐饮住宿类(Q1，良) > 休闲娱乐类(Q3，中)

从总体来看，中山市目前的服务业空间布局与人口分布密度较为符合。其中，公共服务类由生活服务和行政机构组成，同时在前文的最邻近距离分析中“行政机构”得分最高，说明中山市的服务机构配置集聚程度适宜，与住宅人口匹配程度高，在“便民”设施的方面，能够很好地满足居民需求。而耦合度得分最低的休闲娱乐类，由旅游景点、运动健身组成，同时在前文的最邻近距离分析中“旅游景点”得分最低，说明中山市在休闲网点的布局与住宅人口匹配程度较低，在“悦民”设施的配置中仍有待改进。

不同的服务业网点对消费群体的吸引力不同，为了解细致的人口耦合情况，需要对各类网点的耦合度进行分析。通过计算所有“居住点”人口分布与10类服务业网点的耦合度值，得到中山市服务业网点人口耦合度如表6所示，各镇(区)服务网点耦合度箱线图如图4所示。

Table 6. Population coupling degree of each service industry network of Zhongshan

表6. 中山市各服务业网点人口耦合度

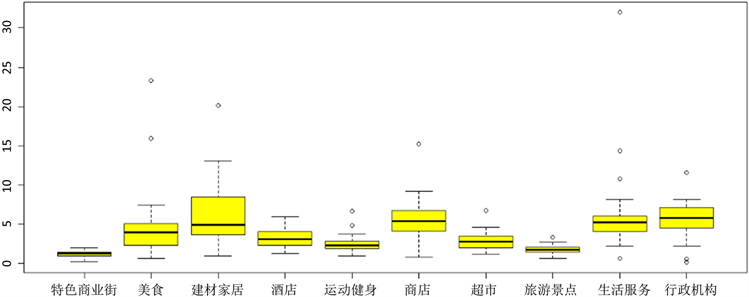
Figure 4. Box diagram of coupling degree of service outlets in towns

图4. 各镇(区)服务网点耦合度箱线图

根据表6和图4，可以得到中山市整体和各镇(区)在不同服务业网点的人口耦合情况。其中，中山市服务业网点人口耦合度最高是行政机构(耦合度为5.25)，耦合等级表现最优，且各镇(区)耦合度集中分布在区间[4.5, 8]内，离散程度相对不高，但存在离群值；中山市服务业网点人口耦合度最低是特色商业街(耦合度为1.15)，耦合等级表现为差，且各镇(区)耦合度集中分布在在区间[1, 3]内，离散程度最低。

这说明，中山市行政机构的整体水平偏高，大部分地区耦合度在高水平范围内略有差异，有个别地区的耦合度与平均水平相比表现欠佳，但整体而言政府服务规划能与人口相匹配，合理地分布在居住点附近；中山市特色商业街的整体水平偏低，各地区之间差异较小，虽然特色商业街的分布集中程度较高、集聚热点在经济发达中心区域和注重旅游业的地区，但是布局密度不合理，不能与人口规模相匹配。

值得留意的是，家居建材为中山市的重要经济来源，在各网点耦合度中仅次于行政机构达到5.15，虽然各地区差异较大，但总体偏高，亦表现为高度耦合；美食、商店、酒店以小型商铺为主的服务业网点，属于城市长尾经济群体，在中山市亦表现出覆盖面广的特点，各镇(区)耦合度集中在较高水平，且没有低水平的离群值，整体人口耦合程度亦表现较好。

为了方便观察耦合度程度高低在空间分布上的差异，本文在此利用克里金空间插值法对各居住点的耦合度进行可视化处理。在此选取行政机构(优，公共服务类)，酒店(良，餐饮住宿类)，特色商业街(差，综合购物类)三种差异较大的服务业网点类型进行示例，得到的服务业网点空间与人口的耦合度示意如图5所示。

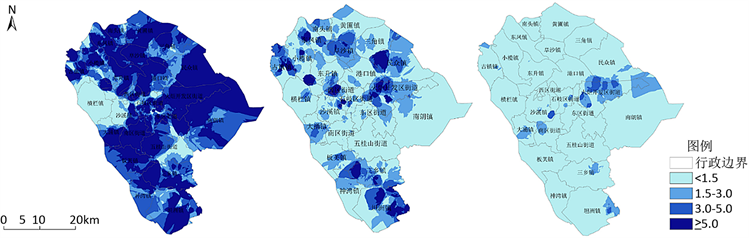
Figure 5. Spatial interpolation of coupling degree

图5. 耦合度空间插值图

从图5可以得知同前文分析一致：表现为优的服务业网点行政机构基本良好覆盖了所有镇(区)；表现为良的服务业网点酒店在发展较差的横栏镇也能较好覆盖，但集中在部分热点区域，比如市界边界和城中心等地区耦合情况较优；表现为差的特色商业街则是在旅游镇(区)和中心区域才相对良好，且整体表现欠佳。

3.4.2. 区域人口耦合度差异性分析

为进一步判断各地区人口耦合度是否适宜，明确调整方向，本文通过异常分析进行地区的差异性分析。由于服务业人口耦合度应满足实际人口的需要，在此选取行政机构(优，公共服务类)，商店(优，综合购物类)，酒店(良，餐饮住宿类)，超市(中，综合购物类)，旅游景点(中，休闲娱乐类)五种使用率相对最高的服务业网点类型进行验证。对五种服务业网点的对各镇(区)的耦合度贡献值与实际常住人口数进行相关性检验，检验结果如表7所示。

Table 7. Correlation test results

表7. 相关性检验结果

** Correlation is significant at the 0.01 level (2-tailed).

由检验结果表明，在0.05的置信水平下，五种服务业网点的人口耦合度贡献值与实际常住人口均存在显著的正比例相关关系，因此可以认为人口越高的镇(区)在这五种耦合度的贡献值越高，与预期一致。由此，可以将实际人口数分别与该五种服务业网点人口耦合度建立简单线性回归模型，并提取各地区的学生化残差以进行异常分析，各镇(区)的具体数据对比如图6所示。

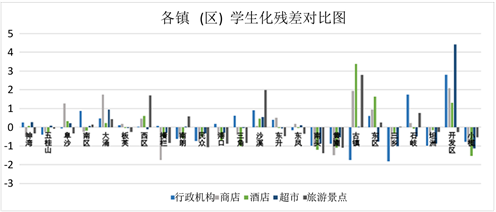
Figure 6. Data comparison chart of towns (actual resident population ranking)

图6. 各镇(区)数据对比图(实际常住人口排序)

由图6可以得到，随着常住人口的增加，耦合度的贡献值呈上升趋势，五种服务业网点的学生化残差基本位于[−3, 3]区间内，并且没有负值的异常值，可以认为中山市在这五类服务业网点的表现上，整体聚集程度适宜并且社区人口的匹配程度良好。

从行政机构网点来看，大部分学生化残差分布在[0.5, −1]区间内，中心城区的火炬开发区和石岐区在该网点上有突出贡献，但是以旅游为建设中心的古镇镇(−1.75)和三乡镇(−1.82)的学生化残差低于一般水平，需要进行调整。

从商店网点来看，除了开发区和古镇表现较为突出外，人口较少的工业建设区阜沙镇和大涌镇在该类网点的耦合情况较优，能够很好地匹配社区居住人口的聚集程度，但是以农业为主的横栏镇的学生化残差最小(−1.75)，远离平均水平，耦合情况欠佳。

从酒店网点来看，古镇镇在该网点的贡献值最大，且学生化残差达到3.38，其他地区的学生化残差集中在[−1.5, 1.5]区间内，耦合匹配程度差异较大。

从超市网点来看，大部分学生化残差分布在[0.5, −1.5]区间内，火炬开发区的贡献显著突出，学生化残差达到4.42，说明中山市这类大型商铺还未在其他地区得到广泛采用，可以在火炬开发区以外的镇(区)进行开发，提升耦合匹配程度。

从旅游景点来看，整体的贡献值均处于较低水平，除了古镇镇的学生化残差接近于3，以文化艺术为特色的沙溪镇学生化残差高达1.99，耦合情况表现较为突出，仍存在很多以旅游为发展方向的地区(如三乡镇)未能达到较好的人口耦合匹配程度。

4. 总结

本文以中山市为研究区，基于手机信令数据提取的居住口径、POI服务业网点数据的位置信息、人口数量等，对中山市服务业空间布局模型进行分析。同时，建立了基于动态聚类法的服务业人口耦合模型，并提出通过构建线性方程进行异常分析，判断各地区的服务业网点人口耦合度的适宜程度，详细分析了调整方向。提供了新型数据在研究城市区域地理信息的使用与分析方法。为提升人口耦合分析效率提供参考。

基金项目

本文的资金项目为广东省级大学生创新创业项目，编号：201910564125。

参考文献

[1]	王芳, 高晓路. 北京市商业空间格局及其与人口耦合关系研究[J]. 城市规划, 2015, 39(11): 23-29.
[2]	Steenbruggen, J., Tranos, E. and Nijkamp, P. (2015) Data from Mobile Phone Operators. Telecommunica-tions Policy, 39, 335-346. https://doi.org/10.1016/j.telpol.2014.04.001
[3]	徐金垒, 萧世伦. 城市海量手机用户停留时空分异分析——以深圳市为例[J]. 地理信息科学, 2015(2): 197-205.
[4]	钟炜菁, 王德, 谢栋灿. 上海市人口分布与空间活动的动态特征研究——基于手机信令数据的探索[J]. 地理研究, 2017, 36(5): 972-984.
[5]	吴丹贤, 周素红. 基于日常购物行为的广州社区居住-商业空间匹配关系[J]. 地理科学, 2017(2): 71-78.
[6]	浩飞龙, 王士君, 冯章献. 基于POI数据的长春市商业空间格局及行业分布[J]. 地理研究, 2018, 37(2): 366-378.
[7]	彭大芹, 罗裕枫, 江德潮. 基于移动信令数据的城市热点识别方法[J]. 重庆邮电大学学报(自然科学版), 2019(2): 95-102.
[8]	钮心毅, 丁亮, 宋小冬. 基于手机数据识别上海中心城的城市空间结构[J]. 城市规划学刊, 2014(6): 61-67.
[9]	张健. 基于POI大数据的城市零售商业空间布局与人口耦合关系研究——以上海市为例[J]. 复旦学报(自然科学版), 2019, 58(2): 151-161.
[10]	熊晶. 粤港澳大湾区发展中的城市发展战略探索——以中山市为例[J]. 广东省社会主义学院学报, 2018(4): 85-89.

为你推荐

友情链接