三次有理B样条曲线及其应用

期刊菜单

三次有理B样条曲线及其应用
Cubic Rational B-Spline Curve and Its Application

DOI: 10.12677/AAM.2020.98157, PDF, HTML, XML, 被引量国家自然科学基金支持
作者: 白根柱：浙江长征职业技术学院基础部，浙江杭州；内蒙古民族大学数理学院，内蒙古通辽
关键词: 有理三次B样条；光滑拼接；轴线异面；管道；Cubic Rational B-Spline Curve； Smooth Blending； Non-Coplana； Tube

摘要: 本文构造了通过给定控制多边形的始末端点且与始末控制多边形相切的一段三次有理B样条曲线，并以三次有理B样条曲线为轴线的管道光滑拼接了轴线异面管道。该方法相较于三段连续的三次均匀B样条曲线为轴线的三段光滑拼接的管道光滑拼接轴线异面管道和两段连续的二次均匀B样条曲线为轴线的两段光滑拼接的管道光滑拼接轴线异面管道其构造简单，易于应用。

Abstract: In this paper, we construct a section of cubic rational B-spline curve which is tangent to the start and end points of the control polygon. Tubes whose axes are in non-coplaner are smoothly blended by tube take cubic rational B-spline curve as its axis. Compared with the three-segment smooth blending tubes with three-segment continuous cubic uniform B-spline curves as the axis between tubes whose axes are non-coplana, and the two-segment smooth blending tubes with quadratic uniform B-spline curves as the axis between tubes whose axes are non-coplana, the proposed method has the advantages of simple structure and easy application.

文章引用：白根柱. 三次有理B样条曲线及其应用[J]. 应用数学进展, 2020, 9(8): 1331-1337. https://doi.org/10.12677/AAM.2020.98157

1. 引言

轴线异面管道光滑拼接是计算几何领域中难点基础问题。我们在基于轴线光滑拼接的管道拼接方面做了诸多尝试 [1] - [7]。Bézier曲线和B样条曲线是构造自由曲线的有力工具，但是Bézier曲线和B样条曲线各有优缺点：Bézier曲线通过控制多边形的两个端点，且与控制多边形的始边和终边相切，不能局部修改；B样条曲线具有局部可修改性，但是不通过控制多边形的始末端点。我们用三点共线方法构造了三段连续的三次均匀B样条曲线光滑拼接两个异面直线，实现了轴线光滑拼接的三段管道拼接。还可以用两重顶点的技术构造三段连续的轴线来构造管道拼接。而用三点共线或两重顶点的技术会增加曲线的段数。用过指定顶点的一段三次均匀B样条曲线拼接异面直线时，在视觉上的光顺性达不到预期。本文拟构造一段过指定顶点的三次均匀有理B样条曲线，并用于轴线异面管道拼接。

2. 过指定顶点的三次有理B样条曲线及其性质

定义1 设

$r (t) = \sum_{i = 0}^{3} N_{i, 3} (t) V_{i + 1}$

和

$r (t) = \frac{\sum_{j = 0}^{3} N_{j, 3} (t) ω_{j} V_{i + j}}{\sum_{j = 0}^{3} N_{j, 3} (t) ω_{j}}$

分别称为三次均匀B样条函数和三次均匀有理B样条函数。其中 $N_{0, 3} (t), N_{1, 3} (t), N_{2, 3} (t), N_{3, 3} (t)$ 为三次均匀B样条基， $V_{0}, V_{1}, V_{2}, V_{3}$ 为特征多边形的顶点。令 $N_{j, 3} (t, w_{0}) = N_{j, 3} w_{j} (j = 0, 1, 2, 3)$ ，则三次均匀有理B样条曲线可表示为

$r (t) = \frac{\sum_{j = 0}^{3} N_{j, 3} (t, ω_{j}) V_{i + j}}{\sum_{j = 0}^{3} N_{j, 3} (t, ω_{j})}$

设 $P_{0}, P_{1}, P_{2}, P_{3}$ 是给定的三次均匀B样条曲线的控制多边形的顶点，构造一段实际控制顶点为 $V_{0}, V_{1}, V_{2}, V_{3}$ 的三次均匀有理B样条曲线，使得端点是 $P_{0}$ 和 $P_{3}$ ，且 $P_{0}$ 和 $P_{3}$ 处的切线分别为 $P_{1} - P_{0}$ 和 $P_{3} - P_{2}$ ，则

${\begin{cases} r (0) = P_{0}, \\ r (1) = P_{3}, \\ r^{'} (0) = P_{1} - P_{0}, \\ r^{'} (1) = P_{3} - P_{2} . \end{cases}$

代入后得

${\begin{cases} V_{0} = \frac{(25 w_{0} + 16 w_{1} - 17 P_{0} w_{2}) P_{0} + (- 7 w_{0} - 28 w_{1} - 7 w_{2}) P_{1} + (2 w_{1} + 8 w_{2} + 2 w_{3}) P_{2} + (10 w_{1} + 16 w_{2} - 2 w_{3}) P_{3}}{18 w_{0}}, \\ V_{1} = - \frac{(2 w_{0} - 16 w_{1} - 10 w_{2}) P_{0} + (- 2 w_{0} - 8 w_{1} - 2 w_{2}) P_{1} + (w_{1} + 4 w_{2} + w_{2}) P_{2} + (5 w_{3} + 5 w_{1} + 8 w_{2} - w_{3}) P_{3}}{18 w_{1}}, \\ V_{2} = \frac{(w_{0} - 8 w_{1} - 5 w_{2}) P_{0} + (- w_{0} - 4 w_{1} - w_{2}) P_{1} + (2 w_{1} + 8 w_{2} + 2 w_{3}) P_{2} + (10 w_{1} + 16 P_{3} w_{2} - 2 w_{3}) P_{3}}{18 w_{2}}, \\ V_{3} = - \frac{(2 w_{0} - 16 w_{1} - 10 w_{2}) P_{0} + (- 2 w_{0} - 8 w_{1} - 2 w_{2}) P_{1} + (7 w_{1} + 28 w_{2} + 7 w_{3}) P_{2} + (17 w_{1} - 16 w_{2} - 25 w_{3}) P_{3}}{18 w_{3}} . \end{cases}$ (1)

将 $P_{0}, P_{1}, P_{2}, P_{3}$ 的坐标 $(P_{1, j}, P_{2, j}, P_{3, j}) (j = 0, 1, 2, 3)$ ，代入，可得所求三次均匀有理B样条曲线的实际控制顶点 $V_{0} (x_{0}, y_{0}, z_{0})$ ， $V_{1} (x_{1}, y_{1}, z_{1})$ ， $V_{2} (x_{2}, y_{2}, z_{2})$ ， $V_{3} (x_{3}, y_{3}, z_{3})$ ，则所求三次均匀有理B样条曲线的参数表达式为

${\begin{cases} x (t, w) = \frac{\sum_{j = 0}^{3} N_{j, 3} (t, w_{j}) x_{j}}{\sum_{j = 0}^{3} N_{j, 3} (t, w_{j})}, \\ y (t, w) = \frac{\sum_{j = 0}^{3} N_{j, 3} (t, w_{j}) y_{j}}{\sum_{j = 0}^{3} N_{j, 3} (t, w_{j})}, \\ z (t, w) = \frac{\sum_{j = 0}^{3} N_{j, 3} (t, w_{j}) z_{j}}{\sum_{j = 0}^{3} N_{j, 3} (t, w_{j})} . \end{cases} t \in [0, 1]$

例1 设 $P_{0} (3, - 3, 0), P_{1} (3, 0, 0), P_{2} (0, 4, 0), P_{3} (0, 4, 3)$ 是给定的点，由式子可以得到端点为 $P_{0}$ 和 $P_{3}$ ，且 $P_{0}$ 和 $P_{3}$ 处的切线分别为 $P_{1} - P_{0}$ 和 $P_{3} - P_{2}$ 的实际控制顶点为 $V_{0} (x_{0}, y_{0}, z_{0})$ ， $V_{1} (x_{1}, y_{1}, z_{1})$ ， $V_{2} (x_{2}, y_{2}, z_{2})$ ， $V_{3} (x_{3}, y_{3}, z_{3})$ 的三次均匀有理B样条曲线。其中 $V_{0}, V_{1}, V_{2}, V_{3}$ 的坐标可表示为：

${\begin{cases} x_{0} = \frac{54 ω_{0} - 36 ω_{1} - 72 ω_{2}}{18 ω_{0}}, \\ y_{0} = \frac{- 75 ω_{0} + 147 ω_{2}}{18 ω_{0}}, \\ z_{0} = \frac{30 ω_{1} + 48 ω_{2} - 6 ω_{3}}{18 ω_{0}} . \end{cases}$ ${\begin{cases} x_{1} = \frac{4 ω_{1} + 2 ω_{2}}{ω_{1}}, \\ y_{1} = - \frac{- 6 ω_{0} + 72 ω_{1} + 78 ω_{2}}{18 ω_{1}}, \\ z_{1} = - \frac{15 ω_{1} + 24 ω_{2} - 3 ω_{3}}{18 ω_{1}} . \end{cases}$

${\begin{cases} x_{2} = - \frac{2 ω_{1} + ω_{2}}{ω_{2}}, \\ y_{2} = \frac{- 3 ω_{0} + 72 ω_{1} + 111 ω_{2}}{18 ω_{2}}, \\ z_{2} = \frac{30 ω_{1} + 48 ω_{2} - 6 ω_{3}}{18 ω_{2}} . \end{cases}$ ${\begin{cases} x_{3} = \frac{4 ω_{1} + 2 ω_{2}}{ω_{3}}, \\ y_{3} = \frac{6 ω_{0} - 144 ω_{1} - 78 ω_{2} + 72_{3}}{18 ω_{3}}, \\ z_{0} = \frac{- 51 ω_{1} + 48 ω_{2} + 75 ω_{3}}{18 ω_{3}} . \end{cases}$

其中 $ω_{0}, ω_{1}, ω_{2}, ω_{3}$ 是权因子。可设 $ω_{0} = ω_{3}$ ，有以下性质：

(1) 当 $| ω_{0} | = | ω_{1} | = | ω_{2} | = | ω_{3} | \geq 1$ 或 $ω_{0}, ω_{1}, ω_{2}, ω_{3} < 0$ 时，是一条过 $P_{0}$ 和 $P_{3}$ ，且 $P_{0}$ 和 $P_{3}$ 处的切线分别为 $P_{1} - P_{0}$ 和 $P_{3} - P_{2}$ 的实际控制顶点为 $V_{0} (x_{0}, y_{0}, z_{0})$ ， $V_{1} (x_{1}, y_{1}, z_{1})$ ， $V_{2} (x_{2}, y_{2}, z_{2})$ ， $V_{3} (x_{3}, y_{3}, z_{3})$ 的三次均匀B样条曲线。

(2) 当 $ω_{0} = ω_{3} = 1, 0 < ω_{1}, ω_{2} < 1$ 时，是一条过 $P_{0}$ 和 $P_{3}$ ，且 $P_{0}$ 和 $P_{3}$ 处的切线分别为 $P_{1} - P_{0}$ 和 $P_{3} - P_{2}$ 的实际控制顶点为 $V_{0} (x_{0}, y_{0}, z_{0})$ ， $V_{1} (x_{1}, y_{1}, z_{1})$ ， $V_{2} (x_{2}, y_{2}, z_{2})$ ， $V_{3} (x_{3}, y_{3}, z_{3})$ 的三次有理B样条曲线， $ω_{1}, ω_{2}$ 越小，曲线越靠近控制多边形的边 $P_{1} P_{2}$ 。

下图1分别为 $ω_{0} = ω_{1} = ω_{2} = ω_{3} = 1$ ， $ω_{0} = ω_{3} = 1, ω_{1} = ω_{2} = \frac{1}{10}$ ， $ω_{0} = ω_{3} = 1, ω_{1} = ω_{2} = \frac{1}{20}$ ， $ω_{0} = ω_{3} = 1, ω_{1} = ω_{2} = \frac{1}{30}$ 和 $ω_{0} = ω_{3} = 1, ω_{1} = ω_{2} = \frac{1}{50}$ 时，过 $P_{0}$ 和 $P_{3}$ ，且 $P_{0}$ 和 $P_{3}$ 处的切线分别为 $P_{1} - P_{0}$ 和 $P_{3} - P_{2}$ 的有理B样条曲线， $0 < ω_{1}, ω_{2} < 1$ 越小曲线越靠近控制多边形的边 $P_{1} P_{2}$ 。

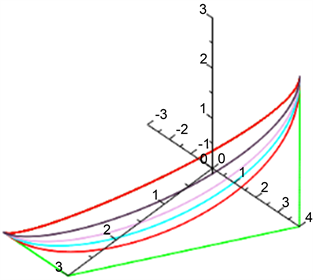
Figure 1. The adjustment function of rational B-spline curve with different weight factor $ω_{0}, ω_{1}, ω_{2}, ω_{3}$

图1. 权因子 $ω_{0}, ω_{1}, ω_{2}, ω_{3}$ 取不同值时，对有理B样条曲线的调节功能

3. 过指定顶点的三次有理B样条曲线及其在轴线异面管道拼接中的应用

在以上讨论中，假设 $P_{0} P_{1}$ 和 $P_{2} P_{3}$ 是异面直线，而三次有理B样条曲线的端点是 $P_{0}$ 和 $P_{3}$ ，且曲线在 $P_{0}$ 和 $P_{3}$ 处分别与 $P_{0} P_{1}$ 和 $P_{2} P_{3}$ 相切。这样，我们可以利用文 [2] 和 [7] 中方法，将此三次均匀有理B样条曲线应用于轴线异面管道拼接中。

例2 设

$Φ_{1} (t, φ) : {\begin{cases} x (t, φ) = 3 + a e_{11} \cdot \sin φ + a e_{21} \cdot \cos φ, \\ y (t, φ) = - 3 + t + a e_{12} \cdot \sin φ + a e_{22} \cdot \cos φ, \\ z (t, φ) = 0 + a e_{13} \cdot \sin φ + a e_{23} \cdot \cos φ . \end{cases} t \in [0, 1], φ \in [0, 2 π]$

和

$Φ_{2} (t, φ) : {\begin{cases} x (t, φ) = 0 + a {e^{'}}_{11} \cdot \sin φ + a {e^{'}}_{21} \cdot \cos φ, \\ y (t, φ) = 4 + a {e^{'}}_{12} \cdot \sin φ + a {e^{'}}_{22} \cdot \cos φ, \\ z (t, φ) = 3 + t + a {e^{'}}_{13} \cdot \sin φ + a {e^{'}}_{23} \cdot \cos φ . \end{cases} t \in [0, 1], φ \in [0, 2 π]$

是两个轴线异面的粗细相同的圆管道。其中 $γ_{1} (t) = {\begin{cases} x_{1} (t) = 3, \\ y_{1} (t) = - 3 + t, \\ z_{1} (t) = 0. \end{cases} γ_{2} (t) = {\begin{cases} x_{2} (t) = 0, \\ y_{2} (t) = 4, \\ z_{2} (t) = 3 + t . \end{cases} t \in [0, 1]$ 为管道 $Φ_{1}, Φ_{2}$ 的轴线的表达式， $E_{i} = (e_{i 1}, e_{i 2}, e_{i 3}), {E^{'}}_{i} = ({e^{'}}_{i 1}, {e^{'}}_{i 2}, {e^{'}}_{i 3}) (i = 1, 2)$ 分别为与轴心垂直平面的单位正交矢量。则光滑拼接两个轴线异面管道 $Φ_{1} (t, φ)$ 和 $Φ_{2} (t, φ)$ 的以三次B样条曲线为轴线的管道的参数表达式为 [2]

$Φ (t, φ) : {\begin{cases} x (t, φ) = x (t) + a B_{1} (t) \sin φ + a N_{1} (t) \cos φ, \\ y (t, φ) = y (t) + a B_{2} (t) \sin φ + a N_{2} (t) \cos φ, \\ z (t, φ) = z (t) + a B_{3} (t) \sin φ + a N_{3} (t) \cos φ . \end{cases} t \in [0, 1], φ \in [0, 2 π]$

其中 $γ (t) = {\begin{cases} x (t), \\ y (t), \\ z (t) . \end{cases}$ 是当 $ω_{0} = ω_{3} = 1, ω_{1} = ω_{2} = \frac{1}{50}$ 时，光滑拼接两个轴线异面管道轴线的三次有理B样条曲线。

$γ (t) : {\begin{cases} x (t) = - \frac{3 (37 t^{3} - 129 t^{2} + 147 t - 55)}{147 t^{2} - 147 t + 55}, \\ y (t) = \frac{424 t^{3} - 645 t^{2} + 666 t - 165}{147 t^{2} - 147 t + 55}, \\ z (t) = \frac{276 t^{3} - 111 t^{2}}{147 t^{2} - 147 t + 55} . \end{cases} t \in [0, 1]$

拼接效果图为图2所示

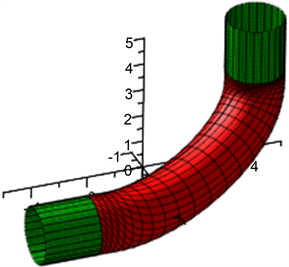
Figure 2. When, $ω_{0} = ω_{3} = 1, ω_{1} = ω_{2} = \frac{1}{50}$ , the effect drawing of circular tube is the same radiuses tube with cubic rational B-spline curve as the axis

图2. $ω_{0} = ω_{3} = 1, ω_{1} = ω_{2} = \frac{1}{50}$ 时，以三次有理B样条曲线为轴线的管道粗细相同圆管道效果图

例3 设

和

$Φ_{2} (t, φ) : {\begin{cases} x (t, φ) = 0 + b {e^{'}}_{11} \cdot \sin φ + b {e^{'}}_{21} \cdot \cos φ, \\ y (t, φ) = 4 + b {e^{'}}_{12} \cdot \sin φ + b {e^{'}}_{22} \cdot \cos φ, \\ z (t, φ) = 3 + t + b {e^{'}}_{13} \cdot \sin φ + b {e^{'}}_{23} \cdot \cos φ . \end{cases} t \in [0, 1], φ \in [0, 2 π]$

$Φ (t, φ) = {\begin{cases} x (t) + d (t) N_{1} (t) \cos φ + d (t) B_{1} (t) \sin φ, \\ y (t) + d (t) N_{2} (t) \cos φ + d (t) B_{2} (t) \sin φ, \\ z (t) + d (t) N_{3} (t) \cos φ + d (t) B_{3} (t) \sin φ . \end{cases} t \in [0, 1], φ \in [0, 2 π] .$

其中 $γ (t) = {\begin{cases} x (t), \\ y (t), \\ z (t) . \end{cases}$ 和 $γ^{'} (t) = {\begin{cases} x^{'} (t), \\ y^{'} (t), \\ z^{'} (t) . \end{cases}$ 是当 $ω_{0} = ω_{3} = 1, ω_{1} = ω_{2} = \frac{1}{50}$ 时，分别光滑拼接两个轴线异面管道轴线

和粗细不同管道某两个母线的三次有理B样条曲线， $d (t) = ‖ γ^{'} (t) - γ (t) ‖$ 。

$γ^{'} (t) = {\begin{cases} x^{'} (t) = - \frac{2 (49 t^{3} - 165 t^{2} + 183 t - 67)}{147 t^{2} - 147 t + 55}, \\ y^{'} (t) = \frac{360 t^{3} - 681 t^{2} + 606 t - 165}{147 t^{2} - 147 t + 55}, \\ z^{'} (t) = \frac{276 t^{3} - 111 t^{2}}{147 t^{2} - 147 t + 55} . \end{cases} t \in [0, 1]$

拼接效果图为图3所示

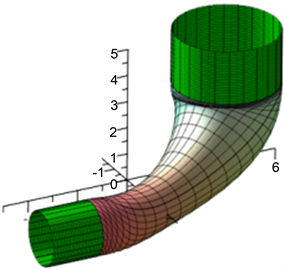
Figure 3. When, $ω_{0} = ω_{3} = 1, ω_{1} = ω_{2} = \frac{1}{50}$ , the effect drawing of circular tube is the different radiuses tube with cubic rational B-spline curve as the axis

图3. $ω_{0} = ω_{3} = 1, ω_{1} = ω_{2} = \frac{1}{50}$ 时，以三次有理B样条曲线为轴线的管道粗细不同圆管道效果图

4. 结束语

我们构造了一段过顶点的三次均匀有理B样条曲线，并将其应用于轴线的圆管道的光滑拼接，其拼接效果很理想。但是，通过选取权因子调整轴线靠近或远离三次有理B样条曲线的控制多边形时，轴线两端点附近的切线发生急剧变化，不能构造光滑拼接两个轴线异面椭圆管道的拼接管道，需要进一步研究。

基金项目

国家自然科学基金项目资助(11561052)，浙江省教育厅一般项目资助Y (201636628)。

参考文献

[1]	Wang, H. and Bai, G.Z. (2013) Employing Generalized Cylindrical Helicoid Tube to Smoothly Blending Tubes Whose Axes Are Non-Coplanar. Applied Mechanics and Materials, 380-384, 1750-1754. https://doi.org/10.4028/www.scientific.net/AMM.380-384.1750
[2]	Bai, G.-Z., Wang, H., et al. (2014) Smoothly Blending of Two Elliptic Cylinders Whose Axes Are Non-Coplanar. Aplied Mechanics and Materials, 309-312, 644-650. https://doi.org/10.4028/www.scientific.net/AMM.644-650.309
[3]	Bai, G.-Z., Liu, S.-Y., Wang, H., W, Z. and Zhao, J.-Y. (2014) A Novel Method for Smooth Blending Cylindrical Surfaces Whose Axes Are Non-Coplanar Based on Smooth Blending Axes. Applied Mechanics and Materials, 687-691, 1470-1473. https://doi.org/10.4028/www.scientific.net/AMM.687-691.1470
[4]	Bai, G.Z., Wu, Z. and Lin, X. (2017) Intersecting Line of Conical Surface and Smoothly Blending of Two Tubes Whose Axes Are Non-Coplanar. Journal of Applied Mathematics and Physics, 5, 1887-1991. https://doi.org/10.4236/jamp.2017.59158
[5]	Bai, G.Z., Wang, H. and Yin, Z.J. (2014) Employing Generalized Bezier Tube to Smoothly Blending Tubes Whose Axes Are Non-Coplanar. Applied Mechanics and Materials, 513-517, 2301-2306. https://doi.org/10.4028/www.scientific.net/AMM.513-517.2301
[6]	Bai, G.Z. and Wang, F. (2019) Application of Quasi-Cubic Bezier Curves in the Blending of Tubes with Different Radiuses. Materials Science and Engineering, Vol. 612, 1-7. https://doi.org/10.1088/1757-899X/612/3/032171
[7]	白根柱. 基于轴线光滑拼接的轴线异面管道拼接技术[J]. 应用数学进展, 2019, 8(7): 1267-1271.

为你推荐

友情链接