1. 引言
随着社会的进步和经济的蓬勃发展,人们通过网络进行货品交易的方式使得交通和物流规划成为一个越来越受人关注的研究课题。最短路径的理论在交通和物流规划中有着广泛的应用。例如Dijkstra算法,Flyod等经典算法被人们沿用至今 [1] [2] [3]。
现代的交通和物流问题往往不是单一的起点和终点的简单的路径规划问题。其中有一类问题叫做具有必经节的路径规划问题 [4] [5]。从起始点到终点的过程中,有多重路径可选,但是有一些节点是必须要经过的节点。即可描述为如何寻找有必经节点的最短路径问题。该类问题的求解方式也较多,但是,在有向图中,必经节点是有顺序的,一旦算出的最短路径中所含必经节点的顺序不符合现实要求,就需要重新规划路径。若不存在符合有向图要求的最短路径,很多算法在发现这个结论前付出了太多的计算代价。针对这一点,本文给出了另一种求解有向图必经节点的方法,可以更早地检验是否存在符合有向图方向要求的必经节点路径。并用实例证实了方法的有效性。
2. 算法介绍
本文给出一种求解有向必经节点的最短路径问题的算法,利用合并节点的技术将问题简化。把求解最短路径的一个问题化为多个小问题来进行求解。成功回避了所求最短路径中不包含必经节点,或者必经节点的顺序不满足方向要求。这个算法还可以快速发现是否存在满足有向图的带有必经节点最短路径存在与否,避免计算代价。
算法步骤
第一步找到所有必经节点,按照已知的路径方向将必经节点排序,将集合记为
,其中
是必经节点,下角标为经过节点的顺序;
第二步将直接连通(中间没有任何其他节点)的若干必经节点合并为一个点(即假设若
和
(
)直接连通,则合并为一个点,记为
);
第三步利用Dijkstra算法寻找每两个必经节点之间的最短路径,(即
与
之间,
,
与
之间,
与
之间,
,
与
之间)及起点到
的最短路径与
到终点之间的最短路径;(若有任何两点之间不存在满足方向的连通路径,则不存在有向最短路径);
第四步把所有最短路径链接起来就构成有向图的最短路径。
3. 一个有向必经节点最短路径问题
如图1所示,这是一个有向网络图。
假设起点为1,终点为11,而路径要求必须经过的节点为3,6,9。两个节点之间的数字代表路径长度。现在,我们要求解经过上述三个必经节点的最短路径。
假设起点为1,终点为11,而路径要求必须经过的节点为3,6,9。两个节点之间的数字代表路径长度。现在,我们要求解经过上述三个必经节点的最短路径。
4. 利用算法求解
首先我们找到图1中所有必经节点,为节点3,6,9。这样我们就找到了必经节点的集合,记为
。如图2所示,有向的带有必经节点的路径为:
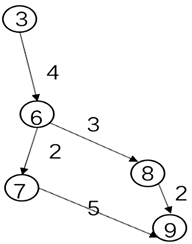
Figure 2. Path diagram of necessary nodes
图2. 必经节点路径图
在这里,节点3和6直接连通,因此合并为一个点,记为36。这样,只剩下两个必经节点,为36和9,(即,
与
合并为
,这时必经节点集合变为
)。如图3所示:
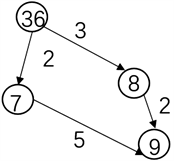
Figure 3. Path diagram of merging necessary nodes
图3. 合并必经节点路径图
接着,利用经典的Dijkstra算法求出合并节点36到9之间的最短路径。为36®8®9。
然后,我们接着使用Dijkstra算法求解出起点1到第一个必经节点3的最短路径为1®2®3。以及最后一个必经节点9到终点的最短路径为9®11。最终,得到该有向必经节点最短路径问题的最短路径为1®2®3®6®8®9®11。
5. 结论
本文给出了一种求解有向必经节点最短路径问题的算法。针对通常的算法存在的求解出的最短路径不满足问题的方向要求,以及花费大量计算才发现路径的不存在的问题。本文给出的算法首先将必经节点排序,并且利用合并连通节点的手段简化了计算。并且,在计算某两个必经节点间最短路径问题时如果无法得出结果,即可以判断出所求最短路径不存在。在后续工作中,我们将对大规模的问题进行计算,检验算法的计算速度。
基金项目
大连民族大学大学生创新创业项目(201912026039,201912026449),大连民族大学理学院信息与计算科学专业建设项目。
NOTES
*通讯作者。