哈密顿算符及其一般运算表达式的分析

期刊菜单

哈密顿算符及其一般运算表达式的分析
General Expression Analysis of the Hamiltonian Operator and Its Formula

DOI: 10.12677/AAM.2020.98150, PDF, HTML, XML, 科研立项经费支持
作者: 冯朝桢：德宏师范高等专科学校理工学院，云南芒市；段卫龙：昆明理工大学城市学院，云南昆明
关键词: 哈密顿算符；拉普拉斯算符；梯度；散度；旋度；Hamiltonian Operators； Laplacian Operator； Gradient； Divergence； Curl

摘要: 哈密顿算符∇及其产生的拉普拉斯算符、梯度、散度和旋度常见运算式在不同曲线坐标系中具体表达式不相同。本文通过定义一个三维正交曲线坐标系(u ₁, u ₂, u ₃)，引入坐标因子h ₁、h ₂、h ₃，推导得到了关于 ∇、 ∇ ∅、 ∇-A、 ∇ΧA、 ∇ ²的一般形式及Poisson方程和Laplace方程的一般表达式。

Abstract: The Hamiltonian operator ∇ and the common expressions such as the Laplacian operator, gradient, divergence, and curl generated by it are not the same in different curve coordinate systems. This paper defines a three-dimensional orthogonal curve coordinate system (u ₁ , u ₂ , u ₃ ), introducing coordinate factor h ₁, h ₂, h ₃, deriving the general form of ∇, ∇ ∅, ∇-A , ∇ ΧA, ∇ ², and the general expression of Poisson equation as well as Laplace equation.

文章引用：冯朝桢, 段卫龙. 哈密顿算符及其一般运算表达式的分析[J]. 应用数学进展, 2020, 9(8): 1286-1291. https://doi.org/10.12677/AAM.2020.98150

1. 引言

哈密顿算符 $\nabla$ 是关于空间的一阶偏微分算子，在数学和物理学中发挥着重要作用。由 $\nabla$ 可以产生一系列的偏微分方程，如泊松方程、拉普拉斯方程等，这些方程在电磁学、热传导等方面经常用到 [1] [2] [3]。 $\nabla$ 及其产生的梯度、散度和旋度等常见运算式在笛卡尔坐标系、柱坐标系、球坐标系、和极坐标系下，其具体表达形式是不一样的，能不能给各种运算式找到一个通用的一般表达式来统一呢？本文针对这个问题做了一些分析，在三维正交曲线坐标系 $(u_{1}, u_{2}, u_{3})$ 下，得到了几个包含哈密顿算符运算式的一般表达式。

2. 正交曲线坐标系

考虑一个由三维正交曲线坐标系 $(u_{1}, u_{2}, u_{3})$ [4] 组成的空间，其中一个无限小的体积元可由 $u_{1}$ ， $u_{1} + d u_{1}$ ， $u_{2}$ ， $u_{2} + d u_{2}$ ， $u_{3}$ ， $u_{3} + d u_{3}$ 相围得到。一般通过 $u_{1}$ 、 $u_{2}$ 、 $u_{3}$ 乘以坐标因子 $h_{1}$ ， $h_{2}$ ， $h_{3}$ 来表示三个方向的距离， $h_{1}$ ， $h_{2}$ ， $h_{3}$ 是 $(u_{1}, u_{2}, u_{3})$ 的函数。

如图1所示，定义三个线元：

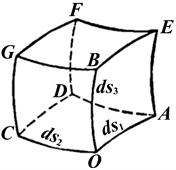
Figure 1. The map of generalized coordinates volume element

图1. 广义坐标系体积元图

$d s_{1} = h_{1} d u_{1}$ ， $d s_{2} = h_{2} d u_{2}$ ， $d s_{3} = h_{3} d u_{3}$ (1.1)

体积元 $d V = d s_{1} d s_{2} d s_{3} = h_{1} h_{2} h_{3} d u_{1} d u_{2} d u_{3}$ ，则哈密顿算符可以表示为：

$\nabla = \frac{\partial}{\partial s_{1}} e_{1} + \frac{\partial}{\partial s_{2}} e_{2} + \frac{\partial}{\partial s_{3}} e_{3} = \frac{\partial}{h_{1} \partial u_{1}} e_{1} + \frac{\partial}{h_{2} \partial u_{2}} e_{2} + \frac{\partial}{h_{3} \partial u_{3}} e_{3}$ (1.2)

$e_{1}$ 、 $e_{2}$ 、 $e_{3}$ 分别是空间变量 $(u_{1}, u_{2}, u_{3})$ 的单位矢量。

1) 一标量 $ϕ$ 在正交曲线坐标系 $(u_{1}, u_{2}, u_{3})$ 连续，一阶微分存在，则根据梯度的定义式， $ϕ$ 的梯度分量：

$\frac{\partial ϕ}{\partial s_{1}} = \frac{\partial ϕ}{h_{1} \partial u_{1}}$ ， $\frac{\partial ϕ}{\partial s_{2}} = \frac{\partial ϕ}{h_{2} \partial u_{2}}$ ， $\frac{\partial ϕ}{\partial s_{3}} = \frac{\partial ϕ}{h_{3} \partial u_{3}}$ (1.3)

$\nabla ϕ = (\frac{\partial ϕ}{h_{1} \partial u_{1}}) e_{1} + (\frac{\partial ϕ}{h_{2} \partial u_{2}}) e_{2} + (\frac{\partial ϕ}{h_{3} \partial u_{3}}) e_{3}$ (1.4)

2) 一矢量 $A$ 在正交曲线坐标系 $(u_{1}, u_{2}, u_{3})$ 连续，一阶微分存在，那么矢量 $A$ 穿过面OCGB和ADFE的向外通量为：

$\frac{\partial}{\partial s_{1}} (A_{1} d s_{2} d s_{3}) d s_{1} = \frac{\partial}{\partial u_{1}} (h_{2} h_{3} A_{1}) d u_{1} d u_{2} d u_{3} = \frac{1}{h_{1} h_{2} h_{3}} \frac{\partial}{\partial u_{1}} (h_{2} h_{3} A_{1}) d V$ (1.5)

用同样的方法可以得到穿过其他4个平面的通量，则根据散度的定义， $A$ 的散度：

$div A = \nabla \cdot A = \frac{1}{h_{1} h_{2} h_{3}} [\frac{\partial}{\partial u_{1}} (h_{2} h_{3} A_{1}) + \frac{\partial}{\partial u_{2}} (h_{3} h_{1} A_{2}) + \frac{\partial}{\partial u_{3}} (h_{1} h_{2} A_{3})]$ (1.6)

3) 矢量 $A$ 是 $(u_{1}, u_{2}, u_{3})$ 的函数，在正交曲线坐标下连续可微， $A_{1}$ 、 $A_{2}$ 、 $A_{3}$ 是沿着 $u_{1}$ 、 $u_{2}$ 、 $u_{3}$ 三个变量方向上的分量，由Stokes定理，在面OADC上 $A_{1}$ 沿着边OA和DC的线积分等于：

$[h_{1} (u_{1}, u_{2}) A_{1} (u_{1}, u_{2}) - h_{1} (u_{1}, u_{2} + d u_{2}) A_{1} (u_{1}, u_{2} + d u_{2})] d u_{1} = - \frac{\partial (h_{1} A_{1})}{\partial u_{2}} d u_{1} d u_{2}$ (1.7)

沿着边AD和CO的线积分等于

$[h_{2} (u_{1} + d u_{1}, u_{2}) A_{2} (u_{1} + d u_{1}, u_{2}) - h_{2} (u_{1}, u_{2}) A_{2} (u_{1}, u_{2})] d u_{2} = \frac{\partial (h_{2} A_{2})}{\partial u_{1}} d u_{1} d u_{2}$ (1.8)

根据Stokes定理， $A$ 沿着面OADC边界上的环路积分等于 $\nabla \times A$ 穿过平面OADC的通量，即：

${(\nabla \times A)}_{3} = \frac{1}{h_{1} h_{2}} [\frac{\partial (h_{2} A_{2})}{\partial u_{1}} - \frac{\partial (h_{1} A_{1})}{\partial u_{2}}]$ (1.9)

对于另外两个面OBGC和OAEB也可以得到

${(\nabla \times A)}_{1} = \frac{1}{h_{2} h_{3}} [\frac{\partial (h_{3} A_{3})}{\partial u_{2}} - \frac{\partial (h_{2} A_{2})}{\partial u_{3}}]$ (1.10)

${(\nabla \times A)}_{2} = \frac{1}{h_{3} h_{1}} [\frac{\partial (h_{1} A_{1})}{\partial u_{3}} - \frac{\partial (h_{3} A_{3})}{\partial u_{1}}]$ (1.11)

所以，矢量 $A$ 的旋度为

$\begin{matrix} curl A = \nabla \times A \\ = \frac{1}{h_{2} h_{3}} [\frac{\partial (h_{3} A_{3})}{\partial u_{2}} - \frac{\partial (h_{2} A_{2})}{\partial u_{3}}] e_{1} + \frac{1}{h_{3} h_{1}} [\frac{\partial (h_{1} A_{1})}{\partial u_{3}} - \frac{\partial (h_{3} A_{3})}{\partial u_{1}}] e_{2} \\ + \frac{1}{h_{1} h_{2}} [\frac{\partial (h_{2} A_{2})}{\partial u_{1}} - \frac{\partial (h_{1} A_{1})}{\partial u_{2}}] e_{3} \end{matrix}$ (1.12)

3. 几例含哈密顿算符的运算式

3.1. Poisson方程和Laplace方程

标量 $ϕ$ 在正交曲线坐标系 $(u_{1}, u_{2}, u_{3})$ 连续可微，存在二阶偏导数，且矢量 $A = ε \nabla ϕ$ (如电势和电场强度)，那么 $\nabla \cdot A$ 等于什么呢？将(1.4)式中3个分量乘以 $ε$ 代替(1.6)式中的 $A_{1}$ 、 $A_{2}$ 、 $A_{3}$ 有：

$\nabla \cdot A = \nabla \cdot ε \nabla ϕ = \frac{1}{h_{1} h_{2} h_{3}} [\frac{\partial}{\partial u_{1}} (\frac{h_{2} h_{3}}{h_{1}} ε \frac{\partial ϕ_{1}}{\partial u_{1}}) + \frac{\partial}{\partial u_{2}} (\frac{h_{3} h_{1}}{h_{2}} ε \frac{\partial ϕ_{2}}{\partial u_{2}}) + \frac{\partial}{\partial u_{3}} (\frac{h_{1} h_{2}}{h_{3}} ε \frac{\partial ϕ_{3}}{\partial u_{3}})]$ (2.1)

若 $\nabla \cdot A = f$ ，且 $f \neq 0$ 则(2.1)式称Poisson方程；若 $f \neq 0$ 则称为Laplace方程，令 $ε = 1$ ，可以得到拉普拉斯算符：

$\nabla^{2} = [\frac{\partial}{\partial u_{1}} (\frac{h_{2} h_{3}}{h_{1}} \frac{\partial}{\partial u_{1}}) + \frac{\partial}{\partial u_{2}} (\frac{h_{3} h_{1}}{h_{2}} \frac{\partial}{\partial u_{2}}) + \frac{\partial}{\partial u_{3}} (\frac{h_{1} h_{2}}{h_{3}} \frac{\partial}{\partial u_{3}})]$ (2.2)

3.2. $\nabla \cdot (μ A) = (\nabla μ) \cdot A + μ (\nabla \cdot A)$

$μ (u_{1}, u_{2}, u_{3})$ 连续可微，由(1.4)和(1.6)式可得到：

$\begin{matrix} \nabla \cdot (μ A) = (\nabla μ) \cdot A + μ (\nabla \cdot A) \\ = [(\frac{\partial μ}{h_{1} \partial u_{1}}) A_{1} + (\frac{\partial μ}{h_{2} \partial u_{2}}) A_{2} + (\frac{\partial μ}{h_{3} \partial u_{3}}) A_{3}] \\ + \frac{μ}{h_{1} h_{2} h_{3}} [\frac{\partial}{\partial u_{1}} (h_{2} h_{3} A_{1}) + \frac{\partial}{\partial u_{2}} (h_{3} h_{1} A_{2}) + \frac{\partial}{\partial u_{3}} (h_{1} h_{2} A_{3})] \end{matrix}$ (2.3)

3.3. $\nabla^{2} A = (\nabla^{2} A_{1}) e_{1} + (\nabla^{2} A_{2}) e_{2} + (\nabla^{2} A_{3}) e_{3}$

由(2.2)式可得：

$\begin{matrix} \nabla^{2} A = (\nabla^{2} A_{1}) e_{1} + (\nabla^{2} A_{2}) e_{2} + (\nabla^{2} A_{3}) e_{3} \\ = [\frac{\partial}{\partial u_{1}} (\frac{h_{2} h_{3}}{h_{1}} \frac{\partial A_{1}}{\partial u_{1}}) + \frac{\partial}{\partial u_{2}} (\frac{h_{3} h_{1}}{h_{2}} \frac{\partial A_{1}}{\partial u_{2}}) + \frac{\partial}{\partial u_{3}} (\frac{h_{1} h_{2}}{h_{3}} \frac{\partial A_{1}}{\partial u_{3}})] e_{1} \\ + [\frac{\partial}{\partial u_{1}} (\frac{h_{2} h_{3}}{h_{1}} \frac{\partial A_{2}}{\partial u_{1}}) + \frac{\partial}{\partial u_{2}} (\frac{h_{3} h_{1}}{h_{2}} \frac{\partial A_{2}}{\partial u_{2}}) + \frac{\partial}{\partial u_{3}} (\frac{h_{1} h_{2}}{h_{3}} \frac{\partial A_{2}}{\partial u_{3}})] e_{2} \\ + [\frac{\partial}{\partial u_{1}} (\frac{h_{2} h_{3}}{h_{1}} \frac{\partial A_{3}}{\partial u_{1}}) + \frac{\partial}{\partial u_{2}} (\frac{h_{3} h_{1}}{h_{2}} \frac{\partial A_{3}}{\partial u_{2}}) + \frac{\partial}{\partial u_{3}} (\frac{h_{1} h_{2}}{h_{3}} \frac{\partial A_{3}}{\partial u_{3}})] e_{3} \end{matrix}$ (2.4)

3.4. $\nabla \times (\nabla \times A) = \nabla (\nabla \cdot A) - \nabla^{2} A$

由(1.4)，(1.6)，(2.4)三式可以得到

$\begin{array}{l} \nabla \times (\nabla \times A) \\ = \nabla (\nabla \cdot A) - \nabla^{2} A \\ = \frac{\partial}{h_{1} \partial u_{1}} {\frac{1}{h_{1} h_{2} h_{3}} [\frac{\partial}{\partial u_{1}} (h_{1} h_{2} A_{1}) + \frac{\partial}{\partial u_{2}} (h_{3} h_{1} A_{2}) + \frac{\partial}{\partial u_{3}} (h_{1} h_{2} A_{3})]} e_{1} \\ + \frac{\partial}{h_{2} \partial u_{2}} {\frac{1}{h_{1} h_{2} h_{3}} [\frac{\partial}{\partial u_{1}} (h_{1} h_{2} A_{1}) + \frac{\partial}{\partial u_{2}} (h_{3} h_{1} A_{2}) + \frac{\partial}{\partial u_{3}} (h_{1} h_{2} A_{3})]} e_{2} \\ + \frac{\partial}{h_{3} \partial u_{3}} {\frac{1}{h_{1} h_{2} h_{3}} [\frac{\partial}{\partial u_{1}} (h_{1} h_{2} A_{1}) + \frac{\partial}{\partial u_{2}} (h_{3} h_{1} A_{2}) + \frac{\partial}{\partial u_{3}} (h_{1} h_{2} A_{3})]} e_{3} \end{array}$

$\begin{array}{l} - [\frac{\partial}{\partial u_{1}} (\frac{h_{2} h_{3}}{h_{1}} \frac{\partial A_{1}}{\partial u_{1}}) + \frac{\partial}{\partial u_{2}} (\frac{h_{3} h_{1}}{h_{2}} \frac{\partial A_{1}}{\partial u_{2}}) + \frac{\partial}{\partial u_{3}} (\frac{h_{1} h_{2}}{h_{3}} \frac{\partial A_{1}}{\partial u_{3}})] e_{1} \\ - [\frac{\partial}{\partial u_{1}} (\frac{h_{2} h_{3}}{h_{1}} \frac{\partial A_{2}}{\partial u_{1}}) + \frac{\partial}{\partial u_{2}} (\frac{h_{3} h_{1}}{h_{2}} \frac{\partial A_{2}}{\partial u_{2}}) + \frac{\partial}{\partial u_{3}} (\frac{h_{1} h_{2}}{h_{3}} \frac{\partial A_{2}}{\partial u_{3}})] e_{2} \\ - [\frac{\partial}{\partial u_{1}} (\frac{h_{2} h_{3}}{h_{1}} \frac{\partial A_{3}}{\partial u_{1}}) + \frac{\partial}{\partial u_{2}} (\frac{h_{3} h_{1}}{h_{2}} \frac{\partial A_{3}}{\partial u_{2}}) + \frac{\partial}{\partial u_{3}} (\frac{h_{1} h_{2}}{h_{3}} \frac{\partial A_{3}}{\partial u_{3}})] e_{3} \end{array}$ (2.5)

3.5. 动量算符 $- i ℏ \nabla$ 与Schrödinger方程

由(1.2)式可知动量算符 $- i ℏ \nabla = - i ℏ (e_{1} \frac{\partial}{h_{1} \partial u_{1}} + e_{2} \frac{\partial}{h_{2} \partial u_{2}} + e_{3} \frac{\partial}{h_{3} \partial u_{3}})$ ，自由粒子波函数 $ψ$ 的波动方程为

$- i ℏ \frac{\partial ψ}{\partial t} = - \frac{ℏ^{2}}{2 m} [\frac{\partial}{\partial u_{1}} (\frac{h_{2} h_{3}}{h_{1}} \frac{\partial ψ}{\partial u_{1}}) + \frac{\partial}{\partial u_{2}} (\frac{h_{3} h_{1}}{h_{2}} \frac{\partial ψ}{\partial u_{2}}) + \frac{\partial}{\partial u_{3}} (\frac{h_{1} h_{2}}{h_{3}} \frac{\partial ψ}{\partial u_{3}})] + V (u_{1}, u_{2}, u_{3}) ψ$ (2.6)

4. 在笛卡尔坐标系、柱坐标系和球坐标系的具体形式

4.1. 笛卡尔坐标系

在笛卡尔坐标系中，坐标因子 $h_{1} = 1$ ， $h_{2} = 1$ ， $h_{3} = 1$ ， $d s_{1} = x$ ， $d s_{2} = y$ ， $d s_{3} = z$ ，则：

$\nabla = \frac{\partial}{\partial s_{1}} e_{1} + \frac{\partial}{\partial s_{2}} e_{2} + \frac{\partial}{\partial s_{3}} e_{3} = \frac{\partial}{\partial x} i + \frac{\partial}{\partial y} j + \frac{\partial}{\partial z} k$

$\nabla ϕ = (\frac{\partial ϕ}{\partial x}) i + (\frac{\partial ϕ}{\partial y}) j + (\frac{\partial ϕ}{\partial z}) k$

$div A = \nabla \cdot A = \frac{\partial A_{x}}{\partial x} + \frac{\partial A_{y}}{\partial y} + \frac{\partial A_{z}}{\partial z}$

$curl A = \nabla \times A = (\frac{\partial A_{z}}{\partial y} - \frac{\partial A_{y}}{\partial z}) i + (\frac{\partial A_{x}}{\partial z} - \frac{\partial A_{z}}{\partial x}) j + (\frac{\partial A_{y}}{\partial x} - \frac{\partial A_{x}}{\partial y}) k$

$\nabla^{2} = \frac{\partial^{2}}{\partial x^{2}} + \frac{\partial^{2}}{\partial y^{2}} + \frac{\partial^{2}}{\partial z^{2}}$

4.2. 柱坐标系

在柱坐标系中，坐标因子 $h_{1} = 1$ ， $h_{2} = ρ$ ， $h_{3} = 1$ ， $d s_{1} = d ρ$ ， $d s_{2} = ρ d φ$ ， $d s_{3} = d z$ 则：

$\nabla = \frac{\partial}{\partial s_{1}} e_{1} + \frac{\partial}{\partial s_{2}} e_{2} + \frac{\partial}{\partial s_{3}} e_{3} = \frac{\partial}{\partial ρ} e_{ρ} + \frac{1}{ρ} \frac{\partial}{\partial φ} e_{φ} + \frac{\partial}{\partial z} e_{z}$

$\nabla ϕ = (\frac{\partial ϕ}{\partial ρ}) e_{ρ} + \frac{1}{ρ} (\frac{\partial ϕ}{\partial φ}) e_{φ} + (\frac{\partial ϕ}{\partial z}) e_{z}$

$div A = \nabla \cdot A = \frac{1}{ρ} \frac{\partial (ρ A_{ρ})}{\partial ρ} + \frac{1}{ρ} \frac{\partial A_{φ}}{\partial φ} + \frac{\partial A_{z}}{\partial z}$

$curl A = \nabla \times A = (\frac{1}{ρ} \frac{\partial A_{z}}{\partial φ} - \frac{\partial A_{φ}}{\partial z}) e_{ρ} + (\frac{\partial A_{ρ}}{\partial z} - \frac{\partial A_{z}}{\partial ρ}) e_{φ} + \frac{1}{ρ} (\frac{\partial (ρ A_{φ})}{\partial ρ} - \frac{\partial A_{ρ}}{\partial φ}) e_{z}$

$\nabla^{2} = \frac{1}{ρ} \frac{\partial}{\partial ρ} (ρ \frac{\partial}{\partial ρ}) + \frac{1}{ρ^{2}} \frac{\partial^{2}}{\partial φ^{2}} + \frac{\partial^{2}}{\partial z^{2}}$

4.3. 球坐标系

球坐标系中，坐标因子 $h_{1} = 1$ ， $h_{2} = r$ ， $h_{3} = r \sin θ$ ， $d s_{1} = d r$ ， $d s_{2} = r d θ$ ， $d s_{3} = r \sin θ d φ$ ，则：

$\nabla = \frac{\partial}{\partial r} e_{r} + \frac{1}{r} \frac{\partial}{\partial θ} e_{θ} + \frac{1}{r \sin θ} \frac{\partial}{\partial φ} e_{φ}$

$\nabla ϕ = (\frac{\partial ϕ}{\partial r}) e_{r} + \frac{1}{r} (\frac{\partial ϕ}{\partial θ}) e_{θ} + \frac{1}{r \sin θ} (\frac{\partial ϕ}{\partial φ}) e_{φ}$

$div A = \nabla \cdot A = \frac{1}{r^{2}} \frac{\partial (r^{2} A_{r})}{\partial r} + \frac{1}{r \sin θ} \frac{\partial (A_{θ} \sin θ)}{\partial θ} + \frac{1}{r \sin θ} \frac{\partial A_{φ}}{\partial φ}$

$curl A = \nabla \times A = \frac{1}{r \sin θ} (\frac{\partial (A_{φ} \sin θ)}{\partial θ} - \frac{\partial A_{θ}}{\partial φ}) e_{r} + \frac{1}{r} (\frac{1}{\sin θ} \frac{\partial A_{r}}{\partial φ} - \frac{\partial (r A_{φ})}{\partial r}) e_{θ} + \frac{1}{r} (\frac{\partial (r A_{θ})}{\partial r} - \frac{\partial A_{r}}{\partial θ}) e_{φ}$

$\nabla^{2} = \frac{1}{r^{2}} \frac{\partial}{\partial r} (r^{2} \frac{\partial}{\partial r}) + \frac{1}{r^{2} \sin θ} \frac{\partial}{\partial θ} (\sin θ \frac{\partial}{\partial θ}) + \frac{1}{r^{2} \sin^{2} θ} \frac{\partial^{2}}{\partial φ^{2}}$

5. 结论

通过定义一个三维正交曲线坐标系 $(u_{1}, u_{2}, u_{3})$ 组成的空间，以及用 $u_{1}$ 、 $u_{2}$ 、 $u_{3}$ 乘以坐标因子 $h_{1}$ 、 $h_{2}$ 、 $h_{3}$ 来表示三个方向的线长， $h_{1}$ 、 $h_{2}$ 、 $h_{3}$ 是 $(u_{1}, u_{2}, u_{3})$ 的函数。定义三个线元 $d s_{1} = h_{1} d u_{1}$ ， $d s_{2} = h_{2} d u_{2}$ ， $d s_{3} = h_{3} d u_{3}$ ，可以得到关于哈密顿算符 $\nabla$ 、 $\nabla ϕ$ 、 $\nabla \cdot A$ 、 $\nabla \times A$ 、 $\nabla^{2}$ 及的一般表达式Poisson方程和Laplace方程的一般表达式。在这些表达式中 $h_{1}$ 、 $h_{2}$ 、 $h_{3}$ 取不同的值，可以演化得到在相应坐标系下的对应运算式。

基金项目

云南省教育厅科学研究基金项目(批准号：2016ZZX047)。

参考文献

[1]	Morales, M., Diaz, R.A. and Herrera, W.J. (2015) Solutions of Laplace’s Equation with Simple Boundary Conditions, and Their Applications for Capacitors with Multiple Symmetries. Journal of Electrostatics, 78, 31-45. https://doi.org/10.1016/j.elstat.2015.09.006
[2]	Polyakov, P.A., Rusakova, N.E. and Samukhina, Y.V. (2015) New Solutions for Charge Distribution on Conductor Surface. Journal of Electrostatics, 77, 147-152. https://doi.org/10.1016/j.elstat.2015.08.003
[3]	Frąckowiaka, A., Wolfersdorfb, J.V. and Ciałkowski, M. (2011) Solution of the Inverse Heat Conduction Problem Described by the Poisson Equation for a Cooled Gas-Turbine Blade. International Journal of Heat and Mass Transfer, 54, 1236-1243. https://doi.org/10.1016/j.ijheatmasstransfer.2010.11.001
[4]	Smythe, W.R. (1989) Static and Dynamic Electricity. 3rd Edition, Taylor & Francis, Abingdon, 50-53.

为你推荐

友情链接