1. 引言
有限元法最初应用于航空器的结构强度计算,随着计算机技术的快速发展和普及,现在有限元方法因其高效已广泛应用于几乎所有的科学技术领城。在力学领域,20世纪40年代这个概念就已经提出,后来开始应用在航天航空领域,此后,该方法得到了进一步的应用。并且开始用温度场、变形场、流体力学、电磁场等计算物理和工程问题 [1]。
铝合金车身覆盖件边缘处容易产生裂纹、加工件成形后回弹、折角处皱褶等现象 [2],因此,铝合金的加工通常分为多步,然后再将两者连接。而磁脉冲辅助冲压成形技术,首先通过传统冲压形成大致的整体框架,然后再局部细化,通过磁脉冲冲压进行二次成形,最终实现所需的成形工艺 [3]。磁脉冲翻边成形工艺与传统的翻边成形工艺相比较,具有较为显著的低成本、高生产效率且能保证零件加工质量等一系列优势 [4]。
本文通过使用ANSYS软件对成形工件表面进行仿真模拟,电磁场仿真模拟是对于放电电压为2.25 kV,工件预制孔直径为100 mm,工件厚度为2 mm的情形下通过画网格的方法得出磁脉冲翻边结果,后处理分析相关的使用性能研究。
2. 磁脉冲成形原理简介
作为一种极具前景的成形工艺,磁脉冲成形技术自由灵活的特点使其具有较高的效能 [5],它通过外部设备对一组电容进行充电。电容器储存一定的电量后,对螺线管线圈放电,巨大的电流迅速流经线圈,与此同时,线圈附近产生相应的电磁场,工件内由于周围的电磁场而产生涡流,根据物理电磁学相关的知识可知:通电导体在电磁场中受到相应力的作用,微观上表现为粒子受洛伦兹力,宏观上金属导体受到安培力。于是工件在线圈电流中产生的磁场中,受到了巨大的安培力,远远超过了材料的屈服极限,从而完成了工件的塑性变形。
3. 有限元模型建立
3.1. 电磁场有限元模型的建立
电磁成形力主要来源于线圈和工件之间的磁场作用,工件与线圈主要几何尺寸如图1所示,线圈为3匝。本文采用ANSYS软件电磁场模块,对线圈及工件进行建模分析,其他压边等模具对磁场影响较小,忽略不计。电磁场模型有限元如图2所示,此模型为对称结构,其中包含线圈、工件以及近端、远端空气采用映射划分的形式,单元形状为矩形,由于近端空气的电磁场分布非常复杂,故采用自由划分的形式,单元形状为不规则的三角形。磁场在空气中存在耗散,因此需要建立空气场,ANSYS软件远端空气场划分必须采用辐射性划分方式。

Figure 2. Finite element mesh diagram for electromagnetic field analysis
图2. 电磁场分析有限单元网格剖分图
3.2. 变形场模型建立
电磁场分析后等到的磁压力作为变形场分析边界条件进行加载,变形场几何模型和有限元模型及图3和图4。使用二维PLANE162单元对称整体变形场区域,凹模以及压块结构由于影响较小定义为刚体,。如下图所示单元格划分:

Figure 4. Model meshing schematic diagram
图4. 模型网格划分示意图
相应磁脉冲变形场的单元类型分配以及材料特性如下表1所示:
工件在电磁力的作用下瞬间变形,成形速度非常快,故在分析变形场时,不应该忽视材料的应变率,在有限元模拟中引进Cowper-Symonds因子,进而实现一定的缩放,有效地提高计算精度,计算公式:
(1)
式中,在此研究中,P = 0.25,C = 6500 S−1,σy为静态拉伸应力。

Table 1. Type of deformation field analysis element and table of material characteristics
表1. 变形场分析单元类型及材料特性表
4. 结果分析与讨论
4.1. 电磁场结果分析
图5为不同时刻磁通密度矢量图。从图中可以看出,四个时刻线圈底部与工件上方的区域磁通密度始终最大,该处的磁感应强度最大,从138 μs到276 μs时刻,线圈与工件的最大磁通密度区域向下有所扩大,磁感线在线圈与工件的间隙内逐渐密集起来,其中工件内的磁感应强度增大,但从276 μs到414 μs时,值得注意的是,在414 μs时刻的磁感线方向发生了改变,因而工件所受的电磁力方向发生改变,可知此时是不利于磁脉冲成形的,从414 μs到552 μs时刻,线圈与工件的磁感线开始变得稀疏,磁感应强度减小。
由此产生的磁场分布如图6所示。本文去一些特征节点所受的磁场力机械分析,由此可以看出,五个节点所受磁场力的变化趋势大致相同,只是在数值大小上有所差异,两侧的节点所受的磁场力小于中间节点的磁场力。
 (a) 138 μs (b) 276 μs
(a) 138 μs (b) 276 μs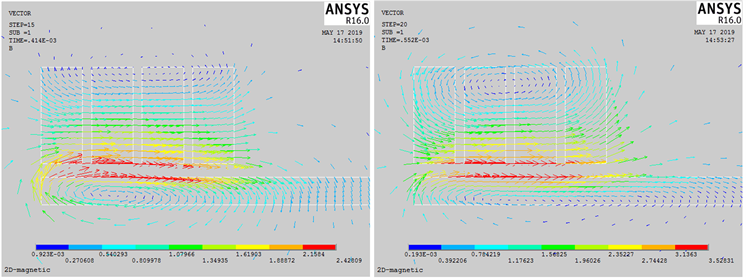 (c) 414 μs (d) 552 μs
(c) 414 μs (d) 552 μs
Figure 5. Vector diagrams of flux density
图5. 磁通密度矢量图
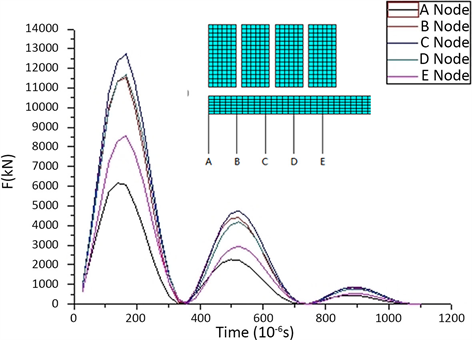
Figure 6. The changing curves of the selected nodes
图6. 节点力变化曲线
4.2. 变形过程
一般采用LS-PrePost软件对于磁脉冲成形变形结果进行提取分析,图7所示的是在放电电压为2.25 kV,工件在不同时刻的塑性应变。工件受到磁场力后,在开始0~100 μs的时间段,工件几乎没有变形,在第110 μs时刻,工件在与凹模圆角接触处产生较小变形,然后在经过约110 μs之后的221 μs时,工件弯曲变得较大,塑性应变也明显增加,最大变形处发生在工件预制孔内边缘处,到达276 μs时,工件再次稍有弯曲,而塑性应变维持不变,在到达331 μs时,工件弯曲程度减小,发生回弹现象,塑性应变略微减少。在整个磁脉冲过程中,与凹模接触的圆角处变形最大,但工件未能成功完全翻边。
 (a) 110 μs
(a) 110 μs  (b) 221 μs
(b) 221 μs  (c) 276 μs
(c) 276 μs 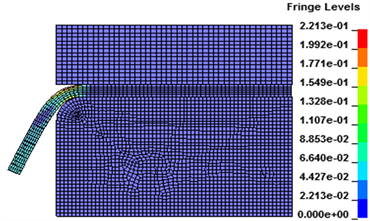 (d) 331 μs
(d) 331 μs
Figure 7. Plastic strain of a workpiece at different times
图7. 不同时刻下工件的塑性应变图
图8所示是工件在2.25 kV放电电压下,不同时刻材料塑性变形速度的云图,从图中观察可以知道,磁场力作用后,在开始的110 μs时,工件变形较轻微,预制孔内侧边缘变形剧烈,速度很快,沿着预制孔内侧向外侧变形速度逐渐减小,等到达221 μs时刻,工件变形较大,速度与上时刻基本保持一致,在276 μs时,工件变形稍有增加,但变形速度有所减小,等到331 μs时翻边完成,工件有些回弹,变形速度变得较小,而此时变形区靠内侧中间的部分是变形速度最大的区域。
图9所示是工件在2.25 kV放电电压下不同时刻工件压力云图。由图可以知道,磁场力作用后,在开始的110 μs时,工件变形幅度还较小,与凹模接触的圆角处是变形主要集中区域,此区域压力最大,上下表面压力的方向相反,在221 μs时,此时工件已经弯曲较大,工件圆角处仍然是压力主要集中处,而且较之前稍有增大,等到276 μs时刻,工件弯曲再度加大,但变形变化不大,压力分布与上时刻基本保持一致,大小略微有减小,331 μs时,翻边结束,压力分布出现较大的变化,最大压力区域转移至预制孔内侧边缘,但整体压力较之前有所减小。
 (a) 110 μs
(a) 110 μs  (b) 221 μs
(b) 221 μs  (c) 276 μs
(c) 276 μs 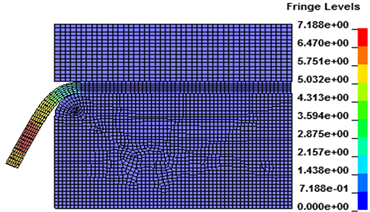 (d) 331 μs
(d) 331 μs
Figure 8. Deformation velocity diagrams at different time
图8. 不同时刻的变形速度图
 (a) 110 μs
(a) 110 μs  (b) 221 μs
(b) 221 μs  (c) 276 μs
(c) 276 μs 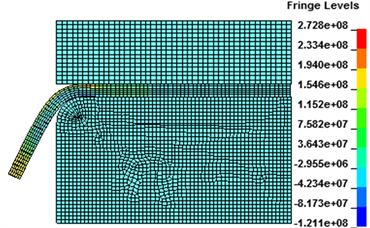 (d) 331 μs
(d) 331 μs
Figure 9. Pressure clouds at different times
图9. 不同时刻的压力云图
在上述仿真实验中,不是理想的结果,工件没有完全翻边实现贴模,初步推测是放电电压较小,所提供的电磁成形力不够使其完全翻边。
4.3. 放电电压对变形影响
为寻找出最佳放电电压,在接下来的实验中每次增加0.25 kV放电电压,一共增加10次至最大放电电压为4.5 kV。结果实验表明,在放电电压为3.00 kV、3.75 kV以及4.50 kV时,工件可以实现完全翻边,如图10所示,而在其他放电电压条件下,工件均不能实现完全翻边。
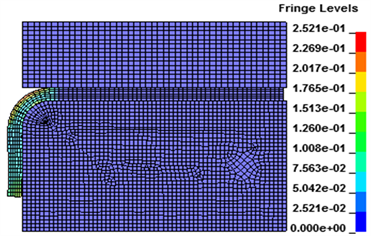 (a) 3.00 kV
(a) 3.00 kV  (b) 3.75 kV
(b) 3.75 kV  (c) 4.50 kV
(c) 4.50 kV
Figure 10. Complete flanging of workpiece under different voltages
图10. 不同电压下工件的完全翻边
虽然3.00 kV、3.75 kV、4.50 kV均能使工件完全翻边,为了找到合适的放电电压,通过实验对比发现,在3.00 kV与4.50 kV的放电条件下,工件完全翻边所用时间为221 μs,而3.75 kV实现完全翻边时间却需要552 μs,考虑能量消耗最小,3.00 kV为本次实验的最佳放电电压。
4.4. 最适放电电压下的工件厚度变化
图11所示是工件在最适放电电压3.00 kV下,各个时刻工件的厚度减薄情况。在第55 μs时,工件变形较小,厚度变化较小,当到达110 μs时,工件开始有所变形,工件厚度变化明显增加,在预制孔内边缘下表面处最为明显,但在工件靠近凹模圆角处的上表面厚度有增加的现象,这是由于在磁脉冲成形过程中,工件该处材料在该时间段里发生了较大的塑性流动,产生了较大的热量,使得材料受热膨胀所致,到达166 μs时,工件继续变形弯曲,厚度减薄继续增加,工件靠近凹模圆角的上表面处变形基本完成,厚度变化很小,最后至221 μs时,工件完全翻成直壁,圆角处厚度基本不变,其他部位厚度减薄持续增加,在预制孔内边缘处最为严重。
 (a) 55 μs
(a) 55 μs 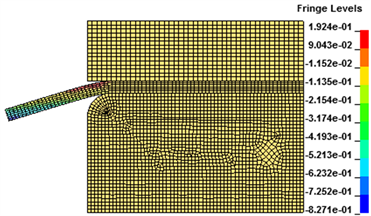 (b) 110 μs
(b) 110 μs  (c) 166 μs
(c) 166 μs  (d) 221 μs
(d) 221 μs
Figure 11. Thickness thinning of workpiece at different time
图11. 不同时刻工件的厚度减薄
5. 结论
1) 在整个翻边过程中,随时间增加工件塑性变形先不断增加然后趋于稳定,最大变形发生在工件预制孔内边缘处。
2) 整个成形阶段中,开始时工件预制孔内侧边缘变形速度很快,沿着预制孔内侧向外侧变形速度逐渐减小,276 μs时变形速度有所减小,331 μs时工件变形速度较小,变形速度最大的区域为变形区靠内侧中间的部分。
3) 通过控制合适的放电电压,能使工件完全翻边且用时较短,实验所得最适放电电压为3.0 kV,此条件下,预制孔内边缘处减薄最严重。

