1. 引言
Hilbert C*-模最初是1953年I. Kaplansky [1] 在交换单位代数上提出的,在20世纪70年代,该理论被拓展到非交换C*-代数。非交换维数是覆盖维数在非交换C*-代数的推广,21世纪初W. Winter提出了完全正秩 [2] 和齐次秩 [3],有力地推动了C*-代数的分类。
在已有理论的基础上,本文研究了Hilbert C*-模上紧算子理想的保持完全正秩和齐次秩的条件,证明了当A的这两种秩不超过n时,
的秩亦不超过n。
2. 预备知识
定义1.1 [2] 设A是C*-代数,F是有限维C*-代数,对
如果
是相互正交的最小投影,则称
是基本集。
定义1.2 [4] 设A,B是C*-代数,
是线性映射且满足对任意的正元
,
也是正元,则称
是正线性映射,若对任意的n,
,
都是正线性映射,则称
是完全正线性映射,简称完全正映射。
定义1.3 [2] 设A是C*-代数,F是有限维C*-代数。对完全正映射
,如果n是满足对F中的任意基本集
都存在
使得
的最小整数,则称
的严格阶等于n。
定义1.4 [2] 设A是C*-代数,如果对任意
,
,都存在对
的关于
的完全正逼近
使得
的严格阶不超过n,则称A的完全正秩小于等于n,记作
。如果n是使得
成立的最小整数,则称
。
定义1.5 [3] 设A是C*-代数,
是完全正映射收缩,
为典范单位嵌入。如果任给
,
,则称
是分段齐次的,如果
是分段齐次的,且
,则称
是严格阶为n的分段齐次。
定义1.6 [3] 设A是C*-代数,如果对任意
,
,都存在对
的关于 的完全正逼近
的完全正逼近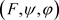 ,使得
,使得 是严格阶不超过n的分段齐次,则称A的齐次秩不超过n,记作
是严格阶不超过n的分段齐次,则称A的齐次秩不超过n,记作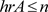 。
。
3. 完全正秩
引理2.1 设A为单的C*-代数,H为可分的Hilbert空间,则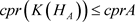 。
。
证明:因为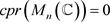 ,由 [2] 命题2.11,
,由 [2] 命题2.11,
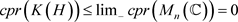 .
.
因为A是单的,由 [3] 定理3.2.4,
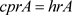 ,
,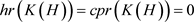 .
.
由 [3] 命题3.1.4,得
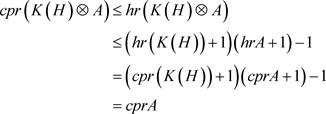 .
.
即
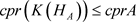 .
.
引理2.2 设A为C*-代数,令 。若任给
。若任给 ,都有
,都有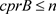 ,则
,则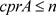 。
。
证明:任给有限集 ,
,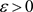 ,令B为F生成的子代数,由
,令B为F生成的子代数,由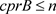 ,对
,对 ,
,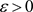 ,存在对F的关于
,存在对F的关于 的完全正逼近
的完全正逼近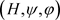 使得
使得
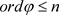 .
.
对 ,由 [5] 定理7.5,存在完全正映射收缩
,由 [5] 定理7.5,存在完全正映射收缩 ,使得
,使得
 ,
,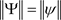 .
.
令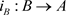 为包含映射,
为包含映射,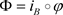 。则
。则 为对F的关于
为对F的关于 的完全正逼近,并且
的完全正逼近,并且 。
。
综上所述, 。
。
引理2.3 设A,F为C*-代数, ,
,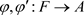 为完全正映射,且满足任给
为完全正映射,且满足任给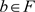 ,
, 。若
。若 且满足
且满足 ,则
,则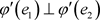 。
。
证明:令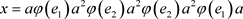 ,则
,则 。而
。而
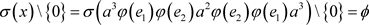 ,
,
所以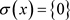 ,得
,得
 ,
,
因此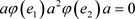 ,即
,即
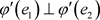 .
.
定理2.4 设A是C*-代数,B为A的遗传子代数,则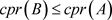 。
。
证明:设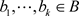 ,存在关于
,存在关于 的完全正逼近
的完全正逼近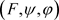 使得
使得
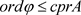 .
.
利用近似单位,可以找到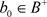 ,
, 使得
使得
任给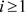 ,
,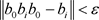 .
.
令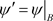 ,
, ,
,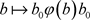 ,则
,则
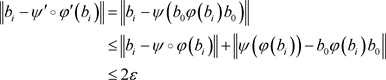 .
.
不妨设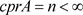 ,则对F的每个基本集
,则对F的每个基本集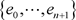 ,存在
,存在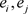 使得
使得
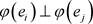 ,
,
由引理2.3,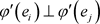 。因此
。因此
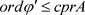 .
.
当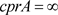 时,显然有
时,显然有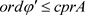 。
。
定理2.5设A为单的C*-代数,E为Hilbert-A模。若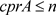 ,则
,则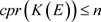 。
。
证明:由引理2.1,有
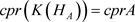 ,
,
E可数生成时, ,所以
,所以
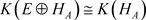 .
.
因为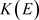 为
为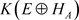 的遗传子代数,由引理2.2得
的遗传子代数,由引理2.2得
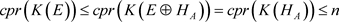 .
.
E为任意Hilbert-A模时:
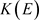 可分时,设
可分时,设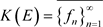 ,由
,由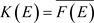 ,存在
,存在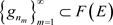 ,使得
,使得
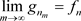 ,
,
设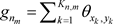 ,
,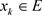 ,
,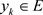 。令
。令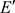 为
为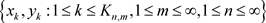 生成的Hilbert-A模。由
生成的Hilbert-A模。由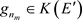 ,得
,得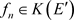 ,所以
,所以 ,又有
,又有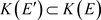 ,所以
,所以 。由
。由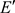 为可数生成,得
为可数生成,得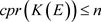 。
。
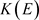 不可分时,
不可分时,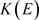 的所有有限生成子代数可分,所以其完全正秩
的所有有限生成子代数可分,所以其完全正秩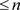 ,由引理2.2,
,由引理2.2,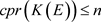 。
。
4. 齐次秩
引理3.1 设A为C*-代数,令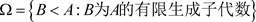 。若任给
。若任给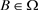 ,都有
,都有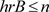 ,则
,则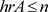 。
。
证明:任给有限集 ,
,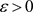 ,令B为F生成的子代数,由
,令B为F生成的子代数,由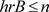 ,对
,对 ,
,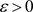 ,存在对F的关于
,存在对F的关于 的完全正逼近
的完全正逼近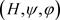 使得
使得
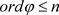 .
.
对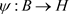 ,由 [5] 定理7.5,存在完全正映射收缩
,由 [5] 定理7.5,存在完全正映射收缩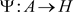 ,使得
,使得
 ,
,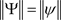 .
.
令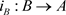 为包含映射,
为包含映射,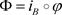 。则
。则 为对F的关于
为对F的关于 的分段齐次的完全正逼近,并且
的分段齐次的完全正逼近,并且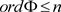 。
。
综上所述,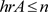 。
。
引理3.2设A,F为C*-代数,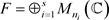 ,
, ,
,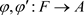 为完全正映射,且满足
为完全正映射,且满足 ,
,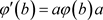 。设
。设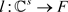 为典范单位嵌入,若
为典范单位嵌入,若 为正元,且满足
为正元,且满足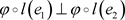 ,则
,则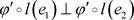 。
。
证明:令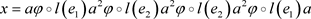 ,则
,则 。而
。而
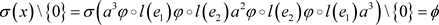 ,
,
所以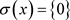 。得
。得
 ,
,
因此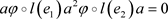 ,即
,即
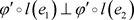 .
.
定理3.3 设A是C*-代数,B为A的遗传子代数,则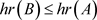 。
。
证明:设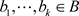 ,存在关于
,存在关于 的完全正逼近
的完全正逼近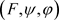 ,
,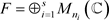 ,使得
,使得
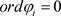 ,
,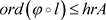 .
.
其中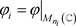 ,
,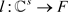 为典范单位嵌入。利用近似单位,可以找到
为典范单位嵌入。利用近似单位,可以找到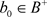 ,
, 使得
使得
任给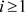 ,
,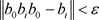 .
.
令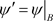 ,
,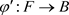 ,
,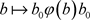 ,则
,则
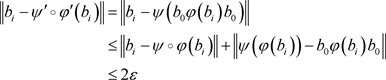 .
.
设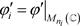 ,则由引理2.3,
,则由引理2.3,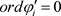 。不妨设
。不妨设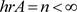 ,则对
,则对 的每个基本集
的每个基本集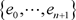 ,存在
,存在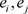 使得
使得
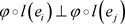 ,
,
由引理3.2,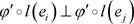 。因此
。因此
 .
.
当 时,显然有
时,显然有 。
。
综上所述,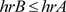 。
。
定理3.4设A为C*-代数,E为Hilbert-A模。若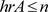 ,则
,则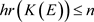 。
。
证明:由 [2] 命题3.1.4,有
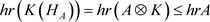 .
.
E可数生成时,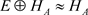 ,所以
,所以
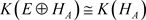 .
.
因为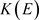 为
为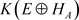 的遗传子代数,由引理3.3得
的遗传子代数,由引理3.3得
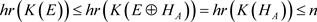 .
.
E为任意Hilbert-A模时:
 可分时,设
可分时,设 ,由
,由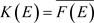 ,存在
,存在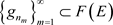 ,使得
,使得
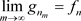 .
.
设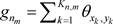 ,
,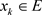 ,
,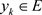 。令
。令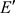 为
为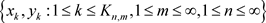 生成的Hilber-A模。由
生成的Hilber-A模。由 ,得
,得 。所以
。所以 ,又有
,又有 ,所以
,所以 。由
。由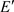 为可数生成,得
为可数生成,得 。
。
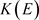 不可分时,
不可分时, 的所有有限生成子代数可分,所以其齐次秩
的所有有限生成子代数可分,所以其齐次秩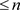 ,由引理3.1,
,由引理3.1,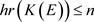 。
。