1. 引言

一百年前，印度著名数学家Ramanujan首次定义了如下经典的Ramanujan和：

$c_q\left(n\right)={\displaystyle \underset{\begin{array}{c}k\mathrm{mod}q\\ \left(k,q\right)=1\end{array}}{\sum }}{\text{e}}^{\frac{2\pi ikn}{q}}\left(q,n\in \mathbb{N}\right)$,(1)

其中 $\mathbb{N}$为正整数集， $\left(k\mathrm{,}q\right)$是k和q的最大公因子。

式(1)满足许多好的性质(见文献 [1]，8.3节)，并且有以下等式成立：

$c_q\left(n\right)={\displaystyle \underset{d|\left(n,q\right)}{\sum }}d\mu \left(\frac{q}{d}\right)$,(2)

其中 $\mu$是经典的Möbius函数。

令d和n都是整数。若 $d\mathrm{<mo>\; |\; </mo>}n$且 $\left(d\mathrm{,}\frac{n}{d}\right)=1$，则称d是n的一个酉因子，并记为 $d\mathrm{<mo>\; |\; </mo>\; <mo>\; |\; </mo>}n$。美国数论学家

E. Cohen [2] 于1959年给出了酉Ramanujan和的定义(也可见文献 [3]，3.2节)

$c_q^{\ast }\left(n\right)={\displaystyle \underset{\begin{array}{c}k\mathrm{mod}q\\ {\left(k,q\right)}_{\ast }=1\end{array}}{\sum }}{\text{e}}^{\frac{2\pi ikn}{q}}\left(q,n\in \mathbb{N}\right)$,(3)

其中 ${\left(k\mathrm{,}q\right)}_{\ast }=\text{max}\left\{d\mathrm{<mo>\; :\; </mo>}d\mathrm{<mo>\; |\; </mo>}k\mathrm{,\; <mi></mi>}d\mathrm{<mo>\; |\; </mo>\; <mo>\; |\; </mo>}q\right\}$。

2. 结果

本部分我们将综述至今为止所得到的有关多元算术函数的Ramanujan展开的结果，这些结果涉及整数环 $\mathbb{Z}$以及有限域上的一元多项式环 $\mathbb{A}={\mathbb{F}}_q\left[T\right]$。

本部分所有结果的证明都能在文末参考文献中找到。

1976年，法国数论学家Delange [4] 在Wintner [5] 结果的基础上证明了定义在 $\mathbb{Z}$上单变量算术函数都可以通过Ramanujan和(1)加以展开。这类似于经典数学分析中周期函数的Fourier展开式。他的结果如下。

定理2.1 (见Delange [4]) 令 $f\mathrm{<mo>\; :\; </mo>}\mathbb{N}\to ℂ$是任一算术函数。如果

${\displaystyle \underset{n=1}{\overset{\infty }{\sum }}}{2}^{\omega \left(n\right)}\frac{\left|\left(\mu \ast f\right)\left(n\right)\right|}{n}<\infty$.

那么对任意的 $n\in \mathbb{N}$，我们有下面绝对收敛的Ramanujan展开式

$f\left(n\right)={\displaystyle \underset{q=1}{\overset{\infty }{\sum }}}{a}_q{c}_q\left(n\right)$,

其中系数 $a_q$从下式中得到

$a_q={\displaystyle \underset{m=1}{\overset{\infty }{\sum }}}\frac{\left(\mu \ast f\right)\left(mq\right)}{mq}\left(q\in \mathbb{N}\right)$.

另外，Delange [4] 还得到定理2.1对于乘性函数的应用。需要指出的是，在Delange [4] 之前，Cohen [6] 也曾对某些特殊的单变量乘性函数类得到了推出绝对收敛的Ramanujan展开式的方法。

Ushiroya [7] 于2016年将定理2.1推广到两个变量的情形，同时得到了定义在 $\mathbb{Z}$上某些特殊函数的经典Ramanujan展开式的具体表达。

在Delange [4] 和Ushiroya [7] 所得结果以及酉Ramanujan和(3)定义的基础上，2018年，匈牙利数论学家Tóth [3] 考虑将定理2.1推广到多元情形，证明了定义在 $\mathbb{Z}$上的多元算术函数都可以通过Ramanujan和(1)与酉Ramanujan和(3)加以展开。

定理2.2 (Tóth [3]，定理2)令 $f\mathrm{<mo>\; :\; </mo>}{\mathbb{N}}^k\to ℂ$是任一算术函数 $\left(k\in \mathbb{N}\right)$。如果

${\displaystyle \underset{n_1,\cdots ,n_k=1}{\overset{\infty }{\sum }}}{2}^{\omega \left(n_1\right)+\cdots +\omega \left(n_k\right)}\frac{\left|\left({\mu }_k\ast f\right)\left(n_1,\cdots ,n_k\right)\right|}{n_1\cdots n_k}<\infty$.(4)

那么对任意的 $n_1\mathrm{,}\cdots \mathrm{,}{n}_k\in \mathbb{N}$，我们有

$f\left(n_1,\cdots ,n_k\right)={\displaystyle \underset{q_1,\cdots ,q_k=1}{\overset{\infty }{\sum }}}{a}_{q_1,\cdots ,q_k}{c}_{q_1}\left(n_1\right)\cdots c_{q_k}\left(n_k\right)$(5)

和

$f\left(n_1,\cdots ,n_k\right)={\displaystyle \underset{q_1,\cdots ,q_k=1}{\overset{\infty }{\sum }}}{a}_{q_1,\cdots ,q_k}^{\ast }{c}_{q_1}^{\ast }\left(n_1\right)\cdots c_{q_k}^{\ast }\left(n_k\right)$,(6)

其中

$\begin{array}{l}{a}_{q_1,\cdots ,q_k}={\displaystyle \underset{m_1,\cdots ,m_k=1}{\overset{\infty }{\sum }}}\frac{\left({\mu }_k\ast f\right)\left(m_1{q}_1,\cdots ,m_k{q}_k\right)}{m_1{q}_1\cdots m_k{q}_k},\\ a_{q_1,\cdots ,q_k}^{\ast }={\displaystyle \underset{\begin{array}{c}{m}_1,\cdots ,m_k=1\\ \left(m_1,q_1\right)=1,\cdots ,\left(m_k,q_k\right)=1\end{array}}{\overset{\infty }{\sum }}\frac{\left({\mu }_k\ast f\right)\left(m_1{q}_1,\cdots ,m_k{q}_k\right)}{m_1{q}_1\cdots m_k{q}_k}}\end{array}$(7)

并且级数(5)和(6)是绝对收敛的。

注2.1. 在定理2.2中令 $k=1$和 $k=2$可以分别得到Delange [4]，Ushiroya [7] 的结论。

$\left(n_1\mathrm{,}\cdots \mathrm{,}{n}_k\right)$记 $n_1\mathrm{,}\cdots \mathrm{,}{n}_k\in \mathbb{N}$的最大公因子，g是从 $\mathbb{N}$到 $ℂ$的算术函数。在定理2.2中令 $f\left(n_1\mathrm{,}\cdots \mathrm{,}{n}_k\right)=g\left(\left(n_1\mathrm{,}\cdots \mathrm{,}{n}_k\right)\right)$，Tóth [3] 进一步得到下面的结果。

定理2.3 (Tóth [3]，定理3) 令 $g\mathrm{<mo>\; :\; </mo>}\mathbb{N}\to ℂ$是一个算术函数且 $k\in \mathbb{N}$。如果

${\displaystyle \underset{n=1}{\overset{\infty }{\sum }}}{2}^{k\omega \left(n\right)}\frac{\left|\left(\mu \ast g\right)\left(n\right)\right|}{n^k}<\infty$.(8)

那么对任意的 $n_1\mathrm{,}\cdots \mathrm{,}{n}_k\in \mathbb{N}$，我们有下面绝对收敛的级数

$g\left(\left(n_1,\cdots ,n_k\right)\right)={\displaystyle \underset{q_1,\cdots ,q_k=1}{\overset{\infty }{\sum }}}{a}_{q_1,\cdots ,q_k}{c}_{q_1}\left(n_1\right)\cdots c_{q_k}\left(n_k\right)$(9)

和

$g\left(\left(n_1,\cdots ,n_k\right)\right)={\displaystyle \underset{q_1,\cdots ,q_k=1}{\overset{\infty }{\sum }}}{a}_{q_1,\cdots ,q_k}^{\ast }{c}_{q_1}^{\ast }\left(n_1\right)\cdots c_{q_k}^{\ast }\left(n_k\right)$,(10)

其中

$\begin{array}{l}{a}_{q_1,\cdots ,q_k}=\frac{1}{Q^k}{\displaystyle \underset{m=1}{\overset{\infty }{\sum }}}\frac{\left(\mu \ast g\right)\left(mQ\right)}{m^k},\\ a_{q_1,\cdots ,q_k}^{\ast }=\frac{1}{Q^k}{\displaystyle \underset{\begin{array}{c}m=1\\ \left(m,Q\right)=1\end{array}}{\overset{\infty }{\sum }}}\frac{\left(\mu \ast g\right)\left(mQ\right)}{m^k}\end{array}$(11)

且 $Q=\left[q_1\mathrm{,}\cdots \mathrm{,}{q}_k\right]$。

注2.2. 注意到乘性函数可以由其在素幂处的值完全确定，由此结果还可进一步得到 $\mathbb{Z}$上某些特殊的多元乘性函数关于经典Ramanujan和以及酉Ramanujan和展开式的具体表达(详见 [3]，推论1和推论2)，更进一步地，它们与经典的Riemann zeta函数 $\zeta \left(z\right)$有关。

设 $A_{+}$是有限域上一元多项式环 $\mathbb{A}={\mathbb{F}}_q\left[T\right]$中首一多项式的全体。类比经典的Ramanujan和(1)，美国著名数论学家L. Carlitz [8] 首次引入 $\mathbb{A}$上的多项式Ramanujan和的定义，然后由E. Cohen在文 [9] 中加以推广。我国数论学家郑志勇教授在最近的文献 [10] 中系统地研究了多项式Ramanujan和的性质。

下面我们简要介绍一下多项式Ramanujan和的定义。假设 $H\left(H\ne 0\right)$是 $\mathbb{A}$中一固定的m次多项式。若

$A\equiv a_{m-1}{T}^{m-1}+\cdots +a_{1}T+a_0\left(\mathrm{mod}\mathrm{<mi></mi>}H\right)$,

则有 $\mathbb{A}$上模H的加性函数

$t\left(A\right)=a_{m-1}$, 对任意的 $A\in \mathbb{A}$.

对任意的 $A\mathrm{,}B\in \mathbb{A}$，我们有

$t\left(A+B\right)=t\left(A\right)+t\left(B\right)$, $t\left(A\right)=t\left(B\right)$如果 $A\equiv B\left(\mathrm{mod}H\right)$,

特别地，如果 $H\mathrm{<mo>\; |\; </mo>}A$，那么 $t\left(A\right)=0$。

对任意给定的 $G\in \mathbb{A}$，令 $t_G\left(A\right)=t\left(GA\right)$，我们可以看出， $t_G\left(A\right)$也是一个模H的加性函数。

再令 $E\left(G\mathrm{,}H\right)\left(A\right)=\lambda \left(t_G\left(A\right)\right)$，其中 $\lambda \left(a\right)={\text{e}}^{2\pi i\left(\frac{\text{tr}\left(a\right)}{p}\right)}\mathrm{<mi></mi>}\left(a\in {\mathbb{F}}_q\right)$， $tr\left(a\right)$是从 ${\mathbb{F}}_q$到 ${\mathbb{F}}_p$的迹函数，则 $E\left(G\mathrm{,}H\right)$是 $\mathbb{A}$上模H的加性特征。

定义2.1 (见Carlitz [8]，(4.1)式或郑志勇 [10]，(1.10)式) 令 ${\mathbb{A}}_{+}$是 $\mathbb{A}$中全体首一多项式构成的集合。对于 $G\mathrm{,}H\in {\mathbb{A}}_{+}$，模H的多项式Ramanujan和 $\eta \left(G,H\right)$定义为

$\eta \left(G,H\right)={\displaystyle \underset{\begin{array}{c}D\mathrm{mod}H\\ \left(D,H\right)=1\end{array}}{\sum }}E\left(G,H\right)\left(D\right)$,(12)

其中 $\left(D,H\right)$是D和H的首一的最大公因子。

注2.3. 郑志勇教授在文 [10] 中研究了许多有关多项式Ramanujan和(12)的性质。

类比酉Ramanujan和的定义(3)，我们下面在 $\mathbb{A}$上定义酉多项式Ramanujan和。

定义2.2 (见齐田芳和胡甦 [11]，定义1.4)对于 $G\mathrm{,}H\in {\mathbb{A}}_{+}$，我们定义 $\mathbb{A}$上的酉多项式Ramanujan和 ${\eta }^{\ast }\left(G\mathrm{,}H\right)$为：

${\eta }^{\ast }\left(G,H\right)={\displaystyle \underset{\begin{array}{c}D\mathrm{<mi></mi>}\mathrm{mod}\mathrm{<mi></mi>}H\\ {\left(D,H\right)}_{\ast }=1\end{array}}{\sum }}E\left(G,H\right)\left(D\right)$,(13)

其中 ${\left(D\mathrm{,}H\right)}_{\ast }=\underset{\text{deg}}{max}\left\{D_1\mathrm{<mo>\; :\; </mo>}{D}_1\mathrm{<mo>\; |\; </mo>}D\mathrm{,}{D}_1\mathrm{<mo>\; |\; </mo>\; <mo>\; |\; </mo>}H\right\}$，即 ${\left(H\mathrm{,}G\right)}_{\ast }$是多项式集合 $\left\{D\mathrm{<mo>\; :\; </mo>}D\mathrm{<mo>\; |\; </mo>}H\mathrm{,}D\mathrm{<mo>\; |\; </mo>\; <mo>\; |\; </mo>}G\right\}$中次数最高的元。

接下来，类比Tóth在文 [3] 中关于数域的工作，我们得到了 $\mathbb{A}$上的多元算术函数(定义见文献 [11]，定义1.5)都可以通过多项式Ramanujan和以及酉多项式Ramanujan和加以展开。我们在文 [11] 中已经得到的结果如下(所涉及到的基本符号见文献 [11] [12])。

定理2.4 (见齐田芳和胡甦 [11]，定理1.7)令 $f\mathrm{<mo>\; :\; </mo>}{\left({\mathbb{A}}_{+}\right)}^k\to ℂ$是任一算术函数， $k\in \mathbb{N}$。如果

${\displaystyle \underset{G_1\mathrm{,}\cdots \mathrm{,}{G}_k\in {\mathbb{A}}_{+}}{\sum }}{2}^{\omega \left(G_1\right)+\cdots +\omega \left(G_k\right)}\frac{\left|\left({\mu }_k\ast f\right)\left(G_1\mathrm{,}\cdots \mathrm{,}{G}_k\right)\right|}{\left|G_1\right|\cdots \left|G_k\right|}<\infty$.(14)

那么对任意的 $G_1\mathrm{,}\cdots \mathrm{,}{G}_k\in {\mathbb{A}}_{+}$，我们有

$f\left(G_1\mathrm{,}\cdots \mathrm{,}{G}_k\right)={\displaystyle \underset{H_1\mathrm{,}\cdots \mathrm{,}{H}_k\in {\mathbb{A}}_{+}}{\sum }}{\mathcal{C}}_{H_1\mathrm{,}\cdots \mathrm{,}{H}_k}\eta \left(G_1\mathrm{,}{H}_1\right)\cdots \eta \left(G_k\mathrm{,}{H}_k\right)$,(15)

和

$f\left(G_1\mathrm{,}\cdots \mathrm{,}{G}_k\right)={\displaystyle \underset{H_1\mathrm{,}\cdots \mathrm{,}{H}_k\in {\mathbb{A}}_{+}}{\sum }}{\mathcal{C}}_{H_1\mathrm{,}\cdots \mathrm{,}{H}_k}^{\ast }{\eta }^{\ast }\left(G_1\mathrm{,}{H}_1\right)\cdots {\eta }^{\ast }\left(G_k\mathrm{,}{H}_k\right)$,(16)

其中

$\begin{array}{l}{\mathcal{C}}_{H_1\mathrm{,}\cdots \mathrm{,}{H}_k}={\displaystyle \underset{M_1\mathrm{,}\cdots \mathrm{,}{M}_k\in {\mathbb{A}}_{+}}{\sum }}\frac{\left({\mu }_k\ast f\right)\left(M_1{H}_1\mathrm{,}\cdots \mathrm{,}{M}_k{H}_k\right)}{\left|M_1{H}_1\right|\cdots \left|M_k{H}_k\right|},\\ {\mathcal{C}}_{H_1\mathrm{,}\cdots \mathrm{,}{H}_k}^{\ast }={\displaystyle \underset{\begin{array}{c}{M}_1\mathrm{,}\cdots \mathrm{,}{M}_k\in {\mathbb{A}}_{+}\\ \left(M_1\mathrm{,}{H}_1\right)=\mathrm{1,}\cdots \mathrm{,}\left(M_k\mathrm{,}{H}_k\right)=1\end{array}}{\sum }}\frac{\left({\mu }_k\ast f\right)\left(M_1{H}_1\mathrm{,}\cdots \mathrm{,}{M}_k{H}_k\right)}{\left|M_1{H}_1\right|\cdots \left|M_k{H}_k\right|}\end{array}$(17)

并且式(15)和(16)都是绝对收敛的。

设g是从 ${\mathbb{A}}_{+}$到 $ℂ$的算术函数。在定理2.4中令 $f\left(G_1\mathrm{,}\cdots \mathrm{,}{G}_k\right)=g\left(\left(G_1\mathrm{,}\cdots \mathrm{,}{G}_k\right)\right)$，这里 $\left(G_1\mathrm{,}\cdots \mathrm{,}{G}_k\right)$是 $G_1\mathrm{,}\cdots \mathrm{,}{G}_k\in {\mathbb{A}}_{+}$的最大公因子，我们在文 [11] 中又得到了下面的结果。

定理2.5 (见齐田芳和胡甦 [11]，定理1.8)设 $g\mathrm{<mo>\; :\; </mo>}{\mathbb{A}}_{+}\to ℂ$是任一算术函数， $k\in \mathbb{N}$。若

${\displaystyle \underset{G\in {\mathbb{A}}_{+}}{\sum }}{2}^{k\omega \left(G\right)}\frac{\left|\left(\mu \ast g\right)\left(G\right)\right|}{{\left|G\right|}^k}<\infty$.(18)

则对任意的 $G_1\mathrm{,}\cdots \mathrm{,}{G}_k\in {\mathbb{A}}_{+}$，我们有下面绝对收敛的级数

$g\left(\left(G_1\mathrm{,}\cdots \mathrm{,}{G}_k\right)\right)\mathrm{<mo>\; =\; </mo>}\underset{}{{\displaystyle {\displaystyle \underset{H_1\mathrm{,}\cdots \mathrm{,}{H}_k\in {\mathbb{A}}_{+}}{\sum }}}}{\mathcal{C}}_{H_1\mathrm{,}\cdots \mathrm{,}{H}_k}\eta \left(G_1\mathrm{,}{H}_1\right)\cdots \eta \left(G_k\mathrm{,}{H}_k\right)$,(19)

和

$g\left(\left(G_1\mathrm{,}\cdots \mathrm{,}{G}_k\right)\right)={\displaystyle \underset{H_1\mathrm{,}\cdots \mathrm{,}{H}_k\in {\mathbb{A}}_{+}}{\sum }}{\mathcal{C}}_{H_1\mathrm{,}\cdots \mathrm{,}{H}_k}^{\ast }{\eta }^{\ast }\left(G_1\mathrm{,}{H}_1\right)\cdots {\eta }^{\ast }\left(G_k\mathrm{,}{H}_k\right)$,(20)

其中

$\begin{array}{l}{\mathcal{C}}_{H_1,\cdots ,H_k}=\frac{1}{{\left|Q\right|}^k}{\displaystyle \underset{M\in {\mathbb{A}}_{+}}{\sum }}\frac{\left(\mu \ast g\right)\left(MQ\right)}{{\left|M\right|}^k},\\ {\mathcal{C}}_{H_1,\cdots ,H_k}^{\ast }=\frac{1}{{\left|Q\right|}^k}{\displaystyle \underset{\begin{array}{c}M\in {\mathbb{A}}_{+}\\ \left(M,Q\right)=1\end{array}}{\sum }}\frac{\left(\mu \ast g\right)\left(MQ\right)}{{\left|M\right|}^k}\end{array}$(21)

且 $Q\mathrm{<mo>\; :\; </mo>}=\left[H_1\mathrm{,}\cdots \mathrm{,}{H}_k\right]$，即Q是 $G_1\mathrm{,}\cdots \mathrm{,}{G}_k\in {\mathbb{A}}_{+}$的最小公倍式 $\left[G_1\mathrm{,}\cdots \mathrm{,}{G}_k\right]$。

注2.4. 注意到 $\mathbb{A}$上的乘性函数都可以由它们在首一不可约多项式处的值完全确定，我们在文 [11] 中将定理2.5应用到乘性函数上，进一步得到了 $\mathbb{A}$上的某些特殊多元乘性函数关于多项式Ramanujan和(12)以及酉多项式Ramanujan和(13)展开式的具体表达(详见 [11]，推论3.4和推论3.5)，并且它们与 $\mathbb{A}$上的Zeta函数

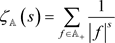
有关(见文献 [11])。

参考文献