1. 引言
偏微分方程 [1] 是纯粹数学和应用数学的一个重要分支,它与化学、物理、金融、医药等自然科学和工程技术的很多领域都有联系,它可分为正问题和反问题,对于绝大多数正问题而言,它们都是Hadamard意义下的适定问题,而大多反问题具有不适定性 [2]。“问题适定性”的概念是著名数学家Hadamard在1923年提出来的,适定性在解决实际问题时具有重要意义,但是随着科学技术的发展,生活中出现了越来越多必须解决的不适定问题,比如,确定散射体的几何形状,医学成像中CT机的发明和应用等等,它们无论在理论上还是实际应用中都是非常重要的。偏微分方程反问题的内容相当丰富,按照数学模型可划分为拋物型方程反问题,双曲型方程反问题,椭圆型方程反问题等三种主要类型,其中抛物型偏微分方程的反问题是近年来研究比较活跃的主题之一,国内外许多学者对此类问题进行了研究并得到了一系列重要成果。例如文献 [3] 考虑了带有积分型源项反演源项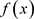 的反问题
的反问题
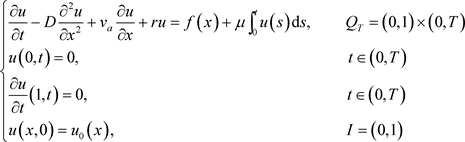 (1.1)
(1.1)
利用最优控制方法证明了解的存在性、唯一性及稳定性。文献 [4] 考虑的一个二阶拋物型方程反演辐射系数的初边值问题:
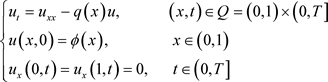 (1.2)
(1.2)
其中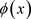 是区间
是区间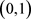 上给定的一个光滑函数,
上给定的一个光滑函数,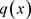 是所要反演的系数,假设给定如下附加条件:
是所要反演的系数,假设给定如下附加条件:
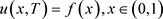 (1.3)
(1.3)
利用最优控制的方法确定满足(1.2)的函数u和q。从物理学上讲,模型(1.2)描述了在均匀介质Q中的热传导过程,所要反演的系数q表示的是热容等导热系数。文献 [5] 则用Tikhonov正则化方法确定了(1.2)的系数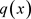 。
。
本文中若无特殊说明,符号C表示各种场合下的不同常数。
本文我们主要研究的是已知终端观测值去反演抛物型方程辐射系数的一个反问题:
问题P:考虑如下二阶拋物型方程的初边值问题:
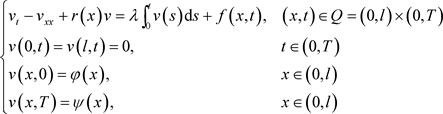 (1.4)
(1.4)
这里的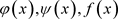 是
是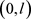 上已知的光滑函数,确定满足(1.4)式的函数v和r,
上已知的光滑函数,确定满足(1.4)式的函数v和r,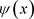 表示在终端时刻
表示在终端时刻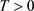 时的观测值,
时的观测值,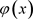 是初始时刻的观测值。
是初始时刻的观测值。
我们主要从理论分析的角度来讨论问题P,在这里我们构造了一个新的控制泛函来代替原来的问题P。
2. 最优控制问题
将确定抛物型方程系数的反问题P重新表述如下最优控制P':
问题P'求 ,使得:
,使得:
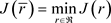 (2.1)
(2.1)
这里
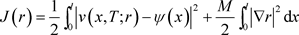 (2.2)
(2.2)
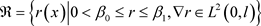 (2.3)
(2.3)
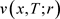 是问题(1.4)的解,
是问题(1.4)的解,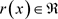 ,M是正则化系数,
,M是正则化系数,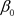 ,
,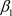 是两个已知正常数。
是两个已知正常数。
引理2.1 [6]:假设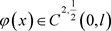 ,对
,对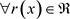 问题(1.4)存在唯一解
问题(1.4)存在唯一解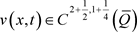 。
。
引理2.2:假设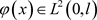 ,对
,对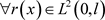 ,存在一个仅T与有关的非负常数C满足下式
,存在一个仅T与有关的非负常数C满足下式
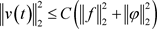 (2.4)
(2.4)
证明:根据问题(1.4)有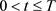
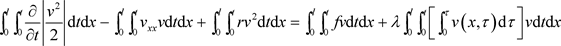
整理得:
则有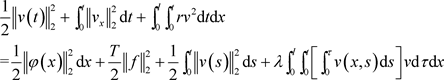
由于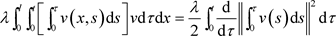 且
且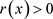 ,
,
从而有
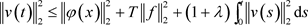
由Gronwall’s不等式得: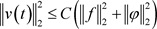
引理2.2即得证。
引理2.3:假设在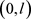 上
上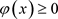 且
且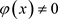 ,
,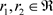 ,
,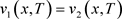 则有
则有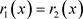 。
。
证明:详细证明可参考 [7] 由于证明过长在此处省略其详细证明过程。
3. 存在性
定理3.1:存在一个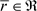 ,使得
,使得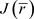 是
是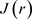 的最小元,即
的最小元,即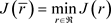 。
。
证明:令 是一个极小化序列,即
是一个极小化序列,即
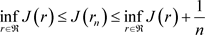 ,
,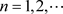
这里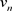 是问题(1.4)的解,
是问题(1.4)的解,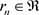 ,易知
,易知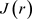 是非负的,且
是非负的,且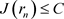 ,可推出:
,可推出:
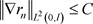 (3.1)
(3.1)
这里C与n无关,由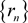 的有界性及(3.1)可得:
的有界性及(3.1)可得:
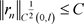 (3.2)
(3.2)
取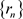 的子序列仍记为
的子序列仍记为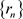 ,使得
,使得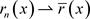 ,
, 。
。
由Sobolev嵌入定理可得:
 (3.3)
(3.3)
因此
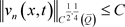 (3.4)
(3.4)
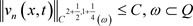 (3.5)
(3.5)
由于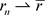 ,从而有
,从而有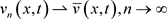 ,容易验证
,容易验证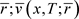 满足问题(1.4),再由Lebesgue’s 控制收敛定理和
满足问题(1.4),再由Lebesgue’s 控制收敛定理和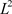 范数的弱半连续性可得:
范数的弱半连续性可得:
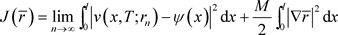
由于
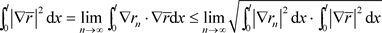
从而有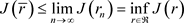
因此有
定理3.1即得证。
4. 必要条件
定理4.1:令r为最优控制问题(2.1)的解,则存在一个三元函数 满足如下方程:
满足如下方程:
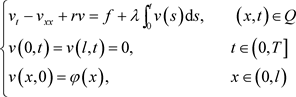 (4.1)
(4.1)
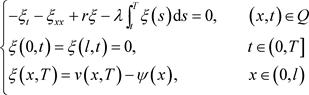 (4.2)
(4.2)
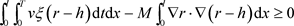 (4.3)
(4.3)
证明: ,
,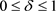 有
有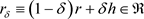 ,则
,则
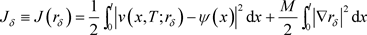 (4.4)
(4.4)
在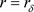 时令
时令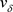 为(1.4)的解,由于r是最优解则有
为(1.4)的解,由于r是最优解则有
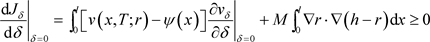 (4.5)
(4.5)
令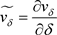 计算得出如下方程:
计算得出如下方程:
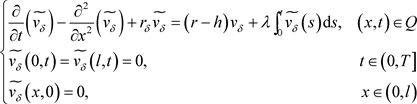 (4.6)
(4.6)
令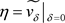 则
则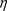 满足
满足
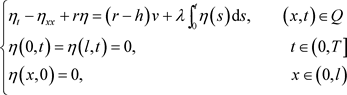 (4.7)
(4.7)
由(4.5)可得:
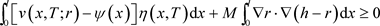 (4.8)
(4.8)
令
假设 是以下问题的解
是以下问题的解
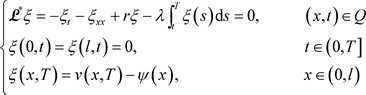 (4.9)
(4.9)
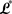 是
是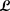 的伴随算子,由(4.7)和(4.9)式可得:
的伴随算子,由(4.7)和(4.9)式可得:
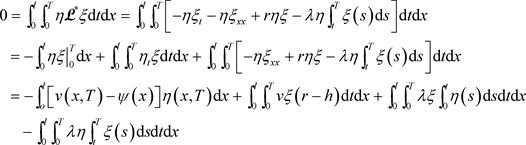
由于
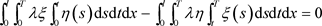
因此
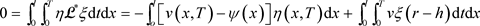 (4.10)
(4.10)
再由(4.8)和(4.10)式可得:
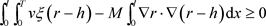
定理4.1即得证。
5. 局部唯一性和稳定性
由于最优控制问题P'是非凸的,故不存在唯一的解,但是当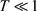 时可证明此解是局部唯一的,且具有稳定性。从而在某种意义下我们将一个不适定问题转化为一个适定的最优控制问题,为数值计算打下了坚实的理论基础。
时可证明此解是局部唯一的,且具有稳定性。从而在某种意义下我们将一个不适定问题转化为一个适定的最优控制问题,为数值计算打下了坚实的理论基础。
引理5.1:对任意有界连续函数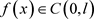 ,有
,有
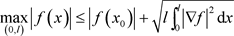 (5.1)
(5.1)
这里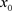 是
是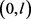 上的不动点。
上的不动点。
证明:因为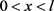 所以有
所以有
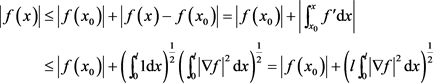
引理5.1即得证。
引理5.2 [8]:设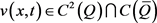 是问题(1.4)的解,则对
是问题(1.4)的解,则对 有如下估计式:
有如下估计式:
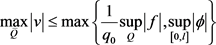 (5.2)
(5.2)
引理5.3:对方程(1.4)4有如下估计:
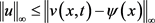 (5.3)
(5.3)
证明过程与引理5.2类似,此处略。
本部分主要证明解得局唯一性和稳定性,假设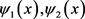 是给定的两个函数,且满足
是给定的两个函数,且满足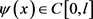 ,令
,令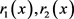 是最优控制问题P'分别对应于
是最优控制问题P'分别对应于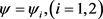 的解,
的解,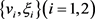 是
是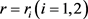 时方程(4.1)和(4.2)的解,其中令
时方程(4.1)和(4.2)的解,其中令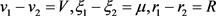 。
。
则v和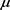 满足
满足
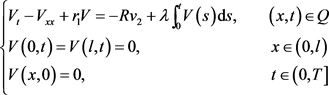 (5.4)
(5.4)
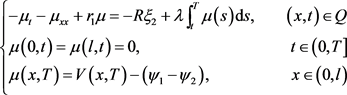 (5.5)
(5.5)
引理5.4:由方程(5.4)可得如下估计:
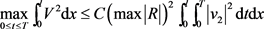 (5.6)
(5.6)
证明:由于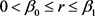 ,
,
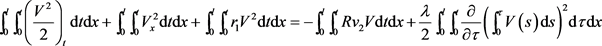
则有
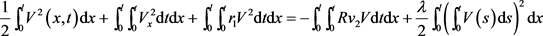
整理得:

从而有
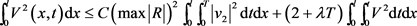
由Gronwall’s不等式得:
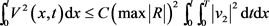
C是T与无关的常数。
引理5.4即得证。
引理5.5:由方程(5.5)可得如下估计:
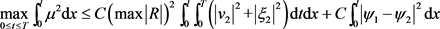 (5.7)
(5.7)
证明:由于 ,由方程(5.5)可得:
,由方程(5.5)可得:
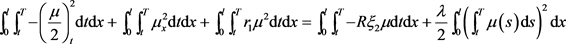
即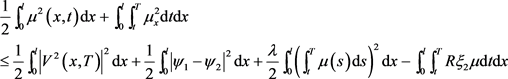
从而有
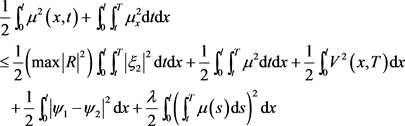
结合(5.6)式可得:
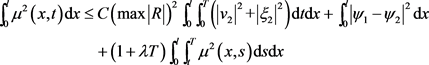
当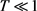 时由Gronwall’s不等式可得:
时由Gronwall’s不等式可得:
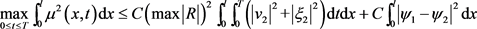
引理5.5即得证。
定理5.4:假设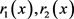 是最优控制问题P'的两个最小值,如果存在
是最优控制问题P'的两个最小值,如果存在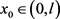 ,使
,使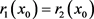 ,当
,当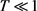 时有
时有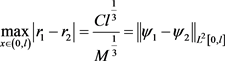 ,对
,对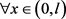 ,这里C与
,这里C与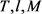 无关。
无关。
证明:在(4.3)式中,当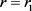 时取
时取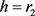 ,当
,当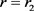 时,取
时,取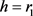 ,则有
,则有
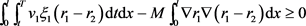 (5.8)
(5.8)
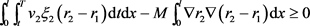 (5.9)
(5.9)
当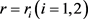 时
时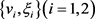 分别是(4.1),(4.2)的解
分别是(4.1),(4.2)的解
由(5.8) + (5.9)得:
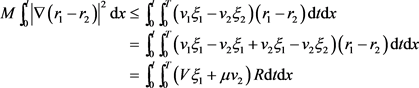 (5.10)
(5.10)
即
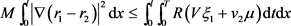 (5.11)
(5.11)
由定理5.4假设知存在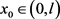 使
使
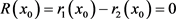 (5.12)
(5.12)
由引理5.1知
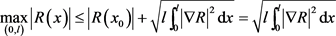 (5.13)
(5.13)
再由(5.10),(5.13)及Young不等式可得:
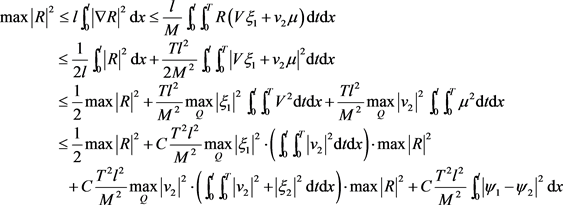 (5.14)
(5.14)
由引理5.2和引理5.3可知
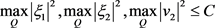 (5.15)
(5.15)
从而根据(5.14),(5.15)式知,
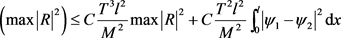 (5.16)
(5.16)
当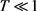 使
使
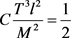 (5.17)
(5.17)
由(5.16)和(5.17)式得:
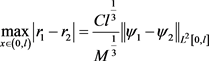 (5.18)
(5.18)
定理5.4即得证。
注:正则化参数的选取在反问题的研究中非常重要,尤其在数值计算中不同的正则化参数会对数值结果产生巨大影响。由定理5.4容易得到如果存在误差界 ,则当正则化参数M以下面方式依赖于误差界并趋于零时,
,则当正则化参数M以下面方式依赖于误差界并趋于零时,
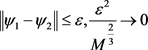
则最优控制解是局部唯一且稳定的。
基金项目
国家自然科学基金资助项目(11461039, 61663018, 11961042);兰州交通大学“百名青年优秀人才培养计划”;甘肃省自然科学基金资助项目(18JR3RA122)。