1. 引言
随着经济发展,我国城市发展日趋迅速,与之相伴的城郊气候对比研究也逐渐成为气象学研究的热点问题。其中针对我国一线城市的成果较多。以北京地区为例,杨萍等人(2013)的研究表明,极端温度事件在城区的强度大于郊区,但与城市热岛效应相关性统计发现,热岛效应对超大市区和郊区影响基本一致 [1]。宋艳玲等人(2003)通过分析城区四个站点与郊区三个站点40年的资料发现,城区气温上升幅度相对郊区明显较大,城、郊降水均略有减小 [2]。而李淼(2011)等人运用小波分析针对北京地区近三百年的降水数据进行了研究,结果表明北京地区年降水量呈缓慢增大趋势 [3]。针对其他一线城市,前人也有相应的研究。程胜龙和王乃昂(2004)针对兰州城市发展研究发现,城市发展对市区气温有增值作用,对市区降水的影响不强烈 [4]。周丽英和杨凯(2001)分析了上海降水百年变化趋势,结果表明市区降水增长率可达郊区的1.5倍,因此城、郊降水差异呈扩大趋势 [5]。而针对本文研究的西安地区,李杨等人(2005)的研究发现,上世纪90年代开始,城市化效应使得郊区温度低于城区,但郊区降水量和相对湿度均高于城区 [6]。前人的城市气候研究,多集中于沿海地区的发达城市,对于西部城市关注较少,而内陆地区独特的大陆性气候会对城市化效应叠加何种扰动,尚不得而知。
陕西省位于中国内陆腹地,地貌种类丰富,气候基本特点为:夏季炎热多雨,冬季寒冷干燥。榆林、汉中均为其地级市(图1),其中榆林位于陕西省北部,北接毛乌素沙地,南邻黄土高原,可作为郊区代表站。而汉中位于陕西省南部,人口密度相对较高,经济较发达,可作为城市代表站。
本文采用滑动t检验和Morlet小波方法,对榆林和汉中夏季气温、降水、风速的时间变化趋势和尺度特征进行对比分析。选用1952~2018年共计67年的月平均资料,首先运用F检验法分析其演变规律,其次利用滑动t检验法确定突变年份,最后利用Morlet小波分析方法确定变化周期。通过两个站点的对比分析,得到城郊气候对比的结果,从而为更深入的认识城郊气候变化差异奠定基础。本文结构安排如下:第2部分介绍了所用的分析方法及数据;第3~5部分分别分析了榆林、汉中两地1952~2018年夏季降水、气温、风速的演变规律;第6部分是全文结论及展望。

Figure 1. Map of Shaanxi Province with Yulin and Hanzhong in red boxes (The image is from http://image.so.com/)
图1. 陕西省地图,红框标注榆林和汉中的位置 (图片来源:http://image.so.com/)
2. 数据和方法
2.1. 数据
本文使用了1952~2018年陕西省榆林、汉中6~8月的月平均降水、气温、风速序列,用6~8月三个月的平均代表每个城市的夏季(下同)。将榆林看作郊区、汉中看作城区。数据来源于中国气象数据网(http://data.cma.cn/)中的中国地面国际交换站气候资料月值数据集,该数据集于2005年7月26日建立,涵盖中国173个基本、基准气象站。数据来自于各省气象部门上报的地面气象数据月报表,已经过国家气象信息中心较严格的机器质量控制及人工抽查,质量良好。
2.2. 小波分析
谱分析是气象学研究中常用的统计学工具,例如针对某个气象要素将其分解成频率分量,就能看到不同时间尺度的波动在整个时间序列中所起的作用,此即为时间序列的频域分析。针对频域分析的经典做法是傅立叶分析,但由于传统傅立叶分析对于非平稳过程的时域信号无法区分,因此出现了窗口傅立叶变换。利用窗函数将整个时间序列进行预拆分,再进行频域分析,但窗函数的宽度是固定的,难以取得最优,窄窗口适合低频,宽窗口适合高频。针对窗口傅立叶变换的这个局限性,出现了类似于窗函数宽度可调的窗口傅立叶变换的小波分析。小波分析能同时得到时频谱,也可用于突变信号拟合。基于以上优点,小波分析在气象学中广泛应用 [7]。小波分析过程包含两个重要步骤,母小波的选取以及对母小波伸缩平移得到子波 [8] [9] [10]。
2.2.1. 母小波
母小波函数时域中需满足平方可积、绝对可积,频域中需满足容许性条件。母小波的三条基本性质:带通性质、零均值和波动性、“小特性”,即母小波具有波动衰减的性质。
气象领域研究常用的母小波有Morlet小波和墨西哥帽小波(Marr小波)。本文采用Morlet小波。
Morlet小波为复数小波,包含了实部虚部。表达式如下
其中
和
为常数项,选取适合的常数项实现归一化,即:
2.2.2. 子波
引进伸缩因子a和平移因子b对母小波进行处理,从而构成一簇函数系,其中
使能量保持不变。
2.2.3. 小波变换
对于给定的能量有限信号
,小波变换系数
计算如下:
根据上式总结小波分析的基本原理:通过控制伸缩因子a得到信号的高频或低频信息,针对信号的概貌或细节进行分析,实现对信号多时空尺度的分析 [8] [9] [10]。
2.2.4. 小波功率谱边界效应及边界影响e-折曲线
由于小波变换假定数据无限长,因此在处理有限长的时间序列时,功率谱首尾两端会出现误差,这种现象称为边界效应。为了尽量消除边界效应,最常见的方法是对信号进行延拓,本文中采用的方法为零延拓 [11]。
由此,出现了边界影响e-折曲线的概念,它在小波功率谱图中表现为倒锥形。曲线以下部分表明该部分小波功率谱受边界效应影响,所表现出的周期特征不确定性较大。
3. 降水序列趋势分析及小波分析
3.1. 降水序列趋势分析
图2是汉中、榆林两地1952~2018年夏季降水的时间序列,结果表明,汉中降水量总体高于榆林,个别年份(如1958年)汉中降水量可达榆林的三倍,这是由于榆林处于高原区,受下垫面粗糙度影响,降水较少。汉中降水波动较大,但波动频率较低,降水大值出现在1958年、1984年,次大值出现在1956年、1960年、1990年、2000年以及2010年。对降水时间序列一元线性回归显示,汉中降水有缓慢减小的趋势。而榆林降水呈现缓慢增大的趋势。对回归方程进行显著性检验,汉中降水的回归方程的F值为0.9304,没有通过置信度
水平的显著性检验(
)。榆林降水的回归方程的F值为1.3006,同样没有通过置信度为
水平的显著性检验(
)。针对气候状况的变化,利用滑动t检验法对汉中、榆林夏季降水时间序列进行突变分析。分别取滑动步长为5年,10年,15年,20年,25年,以0.05的显著性水平来判别突变,以此选出最强突变年。针对榆林确定了三个最强突变年份,分别是1971年向下突变,2001年向上突变以及2009年的向上突变。而针对汉中确定了两个突变年份,分别是1966年向下突变以及2014年的向上突变。
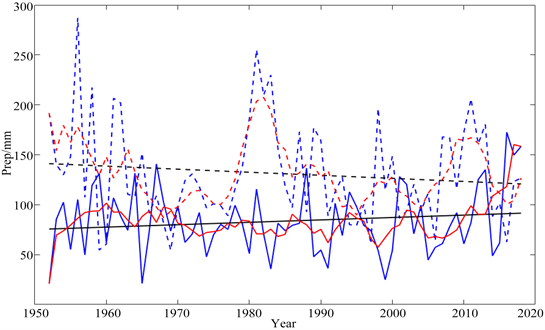
Figure 2. Time series of summer precipitation from 1952 to 2018. The dotted line represents Hanzhong and the solid line represents Yulin. Blue represents the original sequence, black represents unitary linear fitting sequence, and red represents sliding average sequence
图2. 1952~2018年夏季降水时间序列。虚线代表汉中,实线代表榆林。蓝色代表原序列,黑色代表一元线性拟合序列,红色代表滑动平均序列
3.2. 降水序列小波分析
图3为汉中降水序列小波分析结果。信号的强弱分布随着时间发生变化,在整个时间域内,降水主要受三个时间尺度变化所影响,分别为2~5年和7~9年的年际变化以及20~30年的年代际变化,也就是说在年代际尺度中嵌套着年际尺度,但其中20~30年的年代际变化受边界效应的影响,不确定性较大。在置信度检验方面,只有准5年震荡的时间尺度通过了0.05的置信度检验,其中准5年时间尺度在1952~1965、1998~1990以及1998~2000年较强。而年代际尺度在整个事件域均十分明显且较为平稳。
图4为榆林降水序列小波分析结果。结果显示,榆林降水年际变化以2~8年的时间尺度为主,2~8年时间尺度在除了1970~1980以外的年份均较明显。年代际变化特征不明显,年代际尺度上没有明显的周期。

Figure 3. Morlet wavelet analysis of Hanzhong summer precipitation sequence from 1952 to 2018. Above: standardized time series of summer precipitation anomaly (solid red line); Middle left: wavelet power spectrum, black dotted line represents e-folded curve of boundary influence; Center right: time average spectrum (solid blue line), dotted red line is 0.05 confidence line; Bottom: 2~8 years average spectrum (solid blue line), dotted red line is 0.05 confidence line
图3. 1952~2018年汉中夏季降水序列Morlet小波分析。上:夏季降水量距平(红色实线)标准化时间序列;中左:小波功率谱,黑虚线表示边界影响e-折曲线;中右:时间平均谱(蓝色实线),红色虚线为0.05置信度线;下:2~8年平均谱(蓝色实线),红色虚线是0.05置信度线

Figure 4. Same as Figure 3, but Morlet wavelet analysis diagram of Yulin summer precipitation sequence
图4. 同图3,但为榆林夏季降水序列Morlet小波分析图
为了更细致的对时间序列进行分析,将汉中降水序列进行拆分后再进行小波分析。分两种方法,第一种拆分后的序列彼此重复年数尽可能多,分成三段,分别为前50年(1952~2001年)一段,后50年(1969~2018年)一段,以及中间50年(1960~2009年)一段;第二种拆分后的序列彼此没有重复年数,分成三段,前22年(1952~1973年)一段,后22年(1997~2018年)一段,中间22年(1974~1995年)一段。分别针对各段进行小波分析。图5为汉中降水序列拆分后(拆分后序列长度为50年)小波分析的结果,对比来看,年代际尺度嵌套年际尺度的特征三段都较明显。三个时间段的年代际变化均存在32年的时间尺度,但该周期受边界效应影响,不确定性较大。随着时间推移,16年的时间尺度逐步出现并趋于明显,但该周期同样受边界效应影响。1969~2018年中可明显看到16年为周期的震荡。年际变化中,相对拆分前相比,有更多的年份准2~8年震荡通过了0.05的置信度检验。1985~1990年以及1995~2000年这两个时间段,在拆分前序列中2~8年震荡未通过0.05的置信度检验,拆分后随着拆分序列的推移,逐步通过检验,并愈发明显。由此可看出,尽管拆分后的序列重复年份较多,但拆分后序列无论相对于原序列还是拆分后各序列比较,得到的小波分析结果差异却较大,序列的拆分对于小波分析的结果是有影响的。
图6为汉中降水序列拆分后(拆分后序列长度为22年)小波分析的结果,受时间序列长度所限制,年代际时间尺度特征中的准32年周期消失,准16年周期自拆分后的第二个序列出现并在拆分后的第三个序列中平稳且明显。年际变化方面,1952~1973年以2~8年周期为主,而1974~1995年中,仅1988年前后2~8年周期通过了0.05的置信度检验,而在1997~2018年的时间序列中,1997~2001以及2008年前后2~8年周期均通过了0.05的置信度检验。
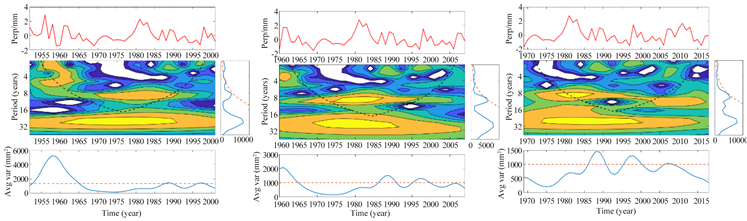
Figure 5. Wavelet analysis diagram of the sequence (length of 50 years) of Hanzhong summer precipitation after decomposition. Left: 1952~2001; middle: 1960~2009; right: 1969~2018
图5. 汉中夏季降水拆分后序列(长度为50年)小波分析图。左:1952~2001年,中:1960~2009年,右:1969~2018年

Figure 6. Wavelet analysis diagram of the sequence (length of 50 years) of Hanzhong summer precipitation after decomposition. Left: 195~1973, center: 1974~1995, right: 1997~2018
图6. 汉中夏季降水拆分后序列(长度为50年)小波分析图。左:1952~1973年,中:1974~1995年,右:1997~2018年
4. 气温序列趋势分析及小波分析
4.1. 气温序列趋势分析
图7是汉中和榆林1952~2018年夏季气温的时间序列,结果显示,汉中气温常年比榆林气温高两度左右,但需要注意的是汉中相对榆林纬度偏南。两地气温波动幅度近似,且均处于缓慢上升状态,汉中气温上升速度大于榆林。榆林气温大值出现在1954年、2000年,次大值出现在1975年前后及2005年前后;汉中气温大值出现时间均滞后于榆林,大值出现在1960年、2008年、2018年,次大值出现在1970年、2000年。汉中气温回归方程的F值为12.9366,通过了置信度为
水平的显著性检验(
),即认为汉中气温增长为可信事件。榆林的回归方程的F值为3.9484,同样通过了置信度为
水平的显著性检验(
),认为榆林气温增长也为可信事件。利用滑动t检验法对汉中、榆林夏季气温时间序列进行突变分析。榆林确定了三个最强突变年份,分别是1976年向下突变,1996年向上突变以及2011年的向上突变。而汉中确定了四个突变年份,分别是1959年向下突变、1971年的向上突变、1994年的向上突变以及2012年的向下突变。

Figure 7. Time series of summer temperature from 1952 to 2018. The dotted line represents Hanzhong and the solid line represents Yulin. Blue represents the original sequence, black represents unitary linear fitting sequence, and red represents sliding average sequence
图7. 1952~2018年夏季气温时间序列。虚线代表汉中,实线代表榆林。蓝色代表原序列,黑色代表一元线性拟合序列,红色代表滑动平均序列
4.2. 气温序列小波分析
图8为汉中气温序列小波分析结果。由小波功率谱可以看出,汉中气温序列的年际年代际变化均没有明显的时间尺度,2~8年方差谱显示,仅个别年份通过了0.05的置信度检验。年代际尺度为准64年周期最强且最平稳,但其位于e-折曲线以下,该周期特征不认为是可信的。
图9为榆林气温序列小波分析结果。结果显示,榆林气温的年际特征以准2年震荡、准5年震荡以及准8年震荡为主,年代际特征中准32年震荡强度较强且十分平稳,但因为边界效应影响,该周期不认为是可信的。除1960年前后、1970年前后,1980~1990年以及2010年以后外,其余年份在2~8年的时间尺度上均通过了0.05的置信度检验。

Figure 8. Morlet wavelet analysis of summer temperature sequence in Hanzhong from 1952 to 2018. Above: standardized time series of summer temperature anomaly (solid red line); Middle left: wavelet power spectrum, black dotted line represents e-folded curve of boundary influence; Center right: time average spectrum (solid blue line), dotted red line is 0.05 confidence line; Bottom: 2~8 years average spectrum (solid blue line), dotted red line is 0.05 confidence line
图8. 1952~2018年汉中夏季气温序列Morlet小波分析。上:夏季气温距平(红色实线)标准化时间序列;中左:小波功率谱,黑虚线表示边界影响e-折曲线;中右:时间平均谱(蓝色实线),红色虚线为0.05置信度线;下:2~8年平均谱(蓝色实线),红色虚线是0.05置信度线

Figure 9. Same as Figure 8, but Morlet wavelet analysis diagram of Yulin summer temperature sequence
图9. 同图8,但为榆林夏季气温序列Morlet小波分析图
5. 风速序列趋势分析及小波分析
5.1. 风速序列趋势分析
图10是汉中、榆林1952~2018年夏季风速的时间序列,汉中风速明显低于榆林,个别年份(如1953年)汉中风速仅为榆林的三分之一,这是由于榆林地形空旷无阻碍且气压差较大。榆林、汉中两地风速波动频率基本一致。榆林风速大值出现在1954年、1970年及2012年,汉中风速大值出现在1970年、1997年及2002年。一元线性回归显示,二者风速均有缓慢增大的趋势。汉中风速回归方程的F值为6.2830,通过了置信度为
水平的显著性检验(
),认为汉中风速缓慢增大为可信事件。榆林风速回归方程的F值为1.3832,没有通过置信度为
水平的显著性检验(
)。突变分析结果表明,榆林确定了四个最强突变年份,分别是1961年向下突变,1967年向上突变,1978年向下突变以及2003年的向上突变。汉中同样确定了四个突变年份,分别是1960年向上突变,1971年向下突变,1993年向上突变以及2005年的向下突变。

Figure 10. Summer wind speed time series 1952~2018. The dotted line represents Hanzhong and the solid line represents Yulin. Blue represents the original sequence, black represents unitary linear fitting sequence, and red represents sliding average sequence
图10. 1952~2018年夏季风速时间序列。虚线代表汉中,实线代表榆林。蓝色代表原序列,黑色代表一元线性拟合序列,红色代表滑动平均序列
5.2. 风速序列小波分析
图11为汉中风速序列小波分析结果。除个别年份的2~8年时间尺度通过0.05的置信度检验,其余年份均没有较明显的年际变化尺度,而年代际尺度中,准32年震荡虽在整个时间域中明显且平稳,但因为边界效应影响,该周期不认为是可信的。准16年震荡在1980年~2000年较明显。
图12为榆林风速序列小波分析结果。榆林的年际变化尺度,仅个别年份存在准2年震荡以及准5年震荡。其中2~8年时间尺度在除了1958年前以及2000年前后较明显外,其余年份均未通过0.05的置信度检验。年代际震荡中,准50年的周期不确定性较大。
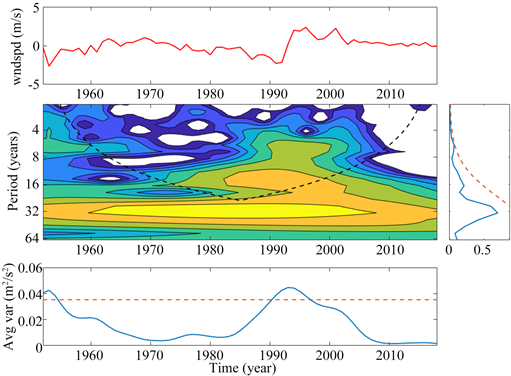
Figure 11. Morlet wavelet analysis of Hanzhong summer wind speed sequence from 1952 to 2018. Above: standardized time series of summer wind speed anomaly (solid red line); Middle left: wavelet power spectrum, black dotted line represents e-folded curve of boundary influence; Center right: time average spectrum (solid blue line), dotted red line is 0.05 confidence line; Bottom: 2~8 years average spectrum (solid blue line), dotted red line is 0.05 confidence line
图11. 1952~2018年汉中夏季风速序列Morlet小波分析。上:夏季风速距平(红色实线)标准化时间序列;中左:小波功率谱,黑虚线表示边界影响e-折曲线;中右:时间平均谱(蓝色实线),红色虚线为0.05置信度线;下:2~8 年平均谱(蓝色实线),红色虚线是0.05置信度线

Figure 12. Same as Figure 11, but Morlet wavelet analysis diagram of Yulin summer wind speed sequence
图12. 同图11,但为榆林夏季风速序列Morlet小波分析图
6. 结论及展望
本文选取陕西省城市代表站汉中和郊区代表站榆林,应用滑动t检验、Morlet小波分析方法对两个站1952~2018年夏季的气温、降水和风速进行对比分析,得到的主要结论如下:
1) 气象要素平均状态城郊对比来看,汉中降水明显多于榆林,汉中气温高于榆林,汉中风速明显小于榆林;
2) 气象要素变化趋势城郊对比来看,汉中降水有缓慢减小的趋势,而榆林降水呈现缓慢增大的趋势。两地气温均有缓慢上升的趋势,两地风速均有缓慢增大的趋势;
3) 时间尺度城郊对比来看,考虑边界效应,汉中夏季降水为准5年周期,榆林夏季降水没有明显的时间尺度特征。汉中夏季气温没有明显的周期特征,榆林夏季气温为准2年周期、准5年周期和准8年周期。汉中夏季风速以及榆林夏季风速均没有明显的周期特征;
4) 汉中降水序列拆分后进行小波分析的结果表明,部分年份拆分前周期不明显,拆分后出现明显的时间尺度特征。
总体而言,陕西省城郊气温、风速的变化趋势基本一致,降水变化趋势相反。汉中各气象要素的变化速度均大于榆林,两地气象要素演变的时间尺度也有较大差异。
本文的研究也存在着明显的缺陷:
1) 郊区和城区各仅用一个气象站代替,气象站个数较少,结果可信度存疑;
2) 汉中相对榆林纬度偏南4˚左右,在气温序列分析中,未能剔除纬度的影响。
致谢
十分感谢中国海洋大学海洋与大气学院的胡瑞金教授。胡瑞金教授创造性地提出的序列拆分,是我成文的基础之一。感谢中国气象局无私的数据提供以及前人宝贵的科研成果。