1. 引言
种群生态问题是生物学研究的焦点内容，利用数学理论和思想构建模型成为生物学研究的重要手段，见文献 [1] [2] [3]。本文旨在介绍和分析单种群生物模型和双种群生物模型的构建过程，是已有文献的有益补充或完善。
借用数学理论和方法，首先阐述了单种群在无限时间内生物量的增长趋势，包括在无限时间生物量无限增长趋势的马尔萨斯模型和生物量有限增长趋势的Logistic模型；随后讨论了两种存在相互竞争和共生关系的生物种群系统，根据变化规律推出相应的生物模型。通过对本文的研读，可促进生物数学初学者对模型内涵的理解，提升对模型的扩展能力。
2. 单一生物种群模型
设该种群生物其繁衍发展不受其他种群的影响，与其它种群生物相互没有迁徙形态。考察物种群体数量在一定环境下的变化，设t时刻该群体生物的总数用
表示。
2.1. 马尔萨斯(Malthus)模型
设物种的生育率b和死亡率d不变，种群的自然增长率
为常数。显然，在时间段
，群体变化量为
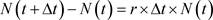
由此得该物种变化方程
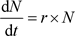(1)
设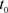
是初始时刻，
，结合(1)式得到
(2)
公式(1)称为马尔萨斯模型，种群函数表达式为(2)。
根据表达式(2)可以得出：随着时间t的增大，种群数量将会趋于无穷大，这是不符合实际的，特别是种群生存资源的有限性没有考虑。说明马尔萨斯模型考虑因素不够全面，不利于长时间预测。
2.2. 在有限空间内的Logistic增长模型
对马尔萨斯模型引入非常数自然增长率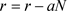
，此时微分方程变为
或
(3)
上式称为Logistic模型。由于(3)式一次项系数为负数，从而种群数量很大时，会对自身数量产生抑制作用。
下面求解模型的种群表达式。将(3)式改写为
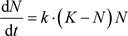
变量分离，得
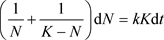
两边积分，得
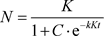
令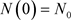
，则
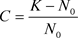
所以(3)式的满足初始条件
的解为
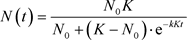
可知
,
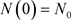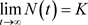由上面得到的种群函数表达式可作出Logistic模型种群曲线，如图1所示。相比于Malthus模型的“J”型无限增长趋势，Logistic模型呈“S”字型增长趋势，一定时间后种群数量将进入饱和期，不会无限增长。
3. 多种群生物模型
3.1. 两物种相互竞争的数学模型
设两种群在同一环境下依赖同一有限资源生存，种群获得的资源与其增长率呈现正相关，如生长在同一块草原上的羊和兔子。设时刻t时两物种群体数分别为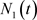
和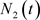
，种群的增长均受到自身规律的制约，自然增长率分别为
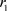和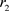
，当对方灭绝时生存数分别
和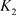
。
设定初始时刻两种群数量均较小。由于开始时资源丰富，第二种群对第一种影响不大，可以认为第一种群以自然增长率增长。但随着两种群繁衍增多，资源减少，第一种群增长减缓，当资源消耗到一定程度，第一种群不再增长，增长率变为0。若第二种群个体消耗资源是第一种群个体消耗的
倍，则第一物种群体的增长率为
类似地，若第一种群个体消耗资源是第二种群个体消耗的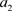
倍，则第二物种群体的增长率为
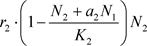
从而，两种群总数
和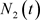
满足下列微分方程组
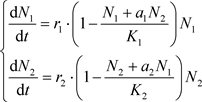(4)
引入
，
，
，
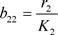(5)
将(5)式代入(4)式得
(6)
赋予种群初值后，方程组(6)即为两物种竞争系统的数学模型。
3.2. 具共生形式的种群数学模型
两个种群共生的现象也是很常见的。如植物与昆虫，昆虫以植物花粉为食，昆虫授粉能加快植物的生长速度，昆虫在没有植物的情况下是无法单独生存的。共生现象可以描述如下：设甲种群能够独立存在并按照Logistic模型的规律发展，乙种群能够为甲种群提供食物，促进甲的增长。
类似于方程(4)，可以写出种群数量演化规律：
(7)
其中
表示单位数量的种群乙可为单位数量的种群甲提供所需要的食物的倍数，上式隐含着种群甲的消失会导致种群乙的灭亡。
设种群乙的死亡率为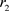
，则其单独自然生存满足
(8)
当种群甲可为种群乙提供食物时，上式右端应加上种群甲对种群乙的增长促进作用，这时有
(9)
由于同时种群乙的增长还受到自身繁衍增长的阻滞作用，所以(9)式右端还应添加Logistic抑制项，这样，方程最终定格为
(10)
表达式(7)和(10)共同构成共生生物系统的数学模型。
4. 小结
种群生态问题是生物学研究的焦点内容，利用数学理论和思想构建模型成为生物学研究的重要手段。本文较详细地介绍了单种群和双种群基本模型的构建过程，可促进初学生物数学者对模型内涵的理解，提升对模型的扩展能力。
基金项目
浙江海洋大学2018年度大学生创新训练计划项目(xj2018097)。
NOTES
*通讯作者。