1. 引言
现在离散数学和组合数学中,把
作为可重复组合的计数公式 [1] [2] [3] [4] [5] ,必须k种元素每一种元素的个数都不小于n,这个公式才成立;任意条件下组合的生成函数在组合数学中已是成熟理论 [1] [2] [3] [4] ,但是任意条件下组合的计数公式还未讨论 [1] [2] [3] [4] [5] ,这里通过发现一些等式推出了此计数公式,提供了一种新证法给大家讨论。并指出了类似的等式大量存在,同时希望更多的人受到启示,在其它方面也能发现类似的等式。现在应用容斥原理证明与本文类似的问题 [6] ,只描述交集或交集之和具有某种特征 [6] ,不能给出具体的集合 [6] ,这里根据参考文献 [7] 发现的等式给出的具体集合,分析了容斥原理证法的不足。
2. 理论探讨
命题:元素
有
个,元素
有
个,元素
有
个……元素
有
个,
,有
个式子相加。
,有
个式子相加。
,有
个式子相加。
……
直到
中的
个式子都没有意义,
中的没有意义的式子等于零。从
-k个元素中取n个元素,共有
种不同的取法。
注释:本文中有
个式子相加(
),是指从
中任意取i个p,共有
种不同方案,每一种方案都与其它的数组成一个式子,共组成
个式子相加,p的值既使有多个相等,但是式子的数量还是
个。证明思路:从
组解中任意取一组解,把i个不满足要求的x值,分别减去对应的p(x的序号与p的序号相同才能相减一次),可得到
组不同的非负整数解,再根据p的序号找到对应的方程(对应方程的解与新解是一一对应的关系),根据对应方程就能知道所取的这组解,在
中的数量。
证明:命题就是求方程①
(
)非负整数解的数量,先求出不满足要求的解的数量,令有
组解,每组解中有一个x的值不满足要求,令有
组解,每组解中有两个x的值不满足要求,……令有
组解,每组解中有b个x的值不满足要求,且b个值是最多的(
)。
是方程①所有不满足要求的解。
的每一组非负整数解,
的值加
可得到
组不同的新解。
的每一组非负整数解,
的值加
可得到
组不同的新解。
……
的每一组非负整数解,
的值加
可得到
组不同的新解。
,有
个式子相加,任意两个式子之间都可能存在相同的新解。
的每一组非负整数解,
的值加
,
的值加
,可得到
组不同的新解。
的每一组非负整数解,
的值加
,
的值加
,可得到
组不同的新解。
……
的每一组非负整数解,
的值加
,
的值加
,可得到
组不同的新解。
,有
个式子相加,任意两个式子之间都可能存在相同的新解。
的每一组非负整数解,
的值加
,
的值加
,
的值加
,可得到
组不同的新解。
的每一组非负整数解,
的值加
,
的值加
,
的值加
,可得到
组不同的新解。
……
的每一组非负整数解,
的值加
,
的值加
,
的值加
,可得到
组不同的新解。
,有
个式子相加,任意两个式子之间都可能存在相同的新解。
……按照上述方法直到求出
中的
个式子相加,任意两个式子之间都可能存在相同的新解。在实际中
都可能存在没有意义的式子,这样的式子等于零,没有意义的式子对应的方程没有非负整数解。
上述方法得到的所有新解,都不满足方程①的要求,令所有新解中不同解的个数是a,则有
,由以下论述可知 中的任意一组解,在新解中都存在,则有
中的任意一组解,在新解中都存在,则有 ,因此
,因此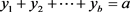 。由于
。由于 可能有多个是相等的,上述方程就可能存在多个方程的解完全相同,任意取一组解,因为p的序号与x的序号相同才可以相加,所以这组解组成的新解是各不相同的,因此把p与x的序号相同作为必要条件,上述方程的任意一组解,只对应一个方程和一组新解。下面就讨论
可能有多个是相等的,上述方程就可能存在多个方程的解完全相同,任意取一组解,因为p的序号与x的序号相同才可以相加,所以这组解组成的新解是各不相同的,因此把p与x的序号相同作为必要条件,上述方程的任意一组解,只对应一个方程和一组新解。下面就讨论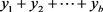 中的每一组解,在新解中存在多少个。
中的每一组解,在新解中存在多少个。
从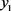 中任意取一组解
中任意取一组解 ,把
,把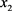 的值减去
的值减去 ,得到的解是方程
,得到的解是方程 的一组解,因此所取的这组解在
的一组解,因此所取的这组解在 组新解中仅有一个,
组新解中仅有一个, 的每一组解都能推出同样的结论。
的每一组解都能推出同样的结论。
从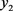 中任意取一组解
中任意取一组解 ,把
,把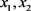 的值任意减去对应的
的值任意减去对应的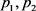 ,可得到
,可得到 组不同的非负整数解,
组不同的非负整数解, 组解分别是(
组解分别是( ),(
),( ),对应的方程分别是
),对应的方程分别是 ,
,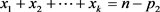 ,
, 组解是(
组解是(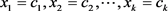 ),对应的方程是
),对应的方程是 ,因此从
,因此从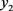 中取的这组解,在
中取的这组解,在 组新解中存在
组新解中存在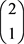 个,在
个,在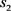 组新解中存在
组新解中存在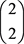 个,
个, 中每一组解都能推出同样的结论。
中每一组解都能推出同样的结论。
从 中任意取一组解
中任意取一组解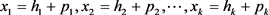 ,把
,把 的值任意减去对应的
的值任意减去对应的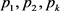 ,可得到
,可得到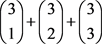 组不同的非负整数解,
组不同的非负整数解, 组解分别是
组解分别是 ,
, ,
, 对应的方程分别是(
对应的方程分别是( ,
, ,
,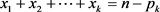 ),
), 组解分别是(
组解分别是( ),(
),( ),(
),( ),对应的方程分别是
),对应的方程分别是 ,
, ,
, 。
。 组解是(
组解是( ),对应的方程是
),对应的方程是 。因此从
。因此从 中取的这组解,在
中取的这组解,在 组新解中有
组新解中有 个,在
个,在 组新解中有
组新解中有 个,在
个,在 组新解中有
组新解中有 个,
个,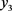 中每一组解都能推出同样的结论。
中每一组解都能推出同样的结论。
……
从 中任意取一组解,同理可知这组解在
中任意取一组解,同理可知这组解在 组新解中有
组新解中有 组,在
组,在 组新解中有
组新解中有 组,……,在
组,……,在 组新解中有
组新解中有 组。
组。
根据以上论述可推出下列b个等式:
1) 
2) 
3) 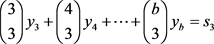
……
b) 

方程①在没有约束条件下,所有非负整数有 组,因此满足约束条件的解有
组,因此满足约束条件的解有 组。
组。
推论:1) ,
, ,
, ,有
,有 个式子相加。
个式子相加。
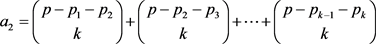 ,有
,有 个式子相加。
个式子相加。
 ,有
,有 个式子相加。
个式子相加。
……
 都可能有没有意义的式子,无意义的式子等于零,
都可能有没有意义的式子,无意义的式子等于零, 都是不小于2的整数,则有:
都是不小于2的整数,则有: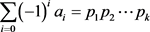
2) 
提示:由命题的组合生成函数可知,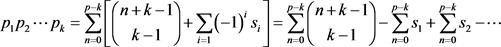 。当
。当 时
时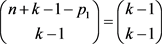 才有意义,因此
才有意义,因此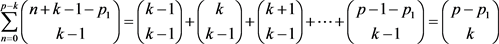 ,因此
,因此 中的每个式子都可以用同样的方法求和。把
中的每个式子都可以用同样的方法求和。把 代入推论1)式可得推论2)式。
代入推论1)式可得推论2)式。
3. 猜想
 ,
, ,
, ,有
,有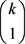 个式子相加。
个式子相加。 ,有
,有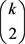 个式子相加。
个式子相加。
 ,有
,有 个式子相加。
个式子相加。
……
 都可能有没有意义的式子,无意义的式子等于零,
都可能有没有意义的式子,无意义的式子等于零,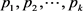 都是不小于2的整数,r是任意非负整数,当
都是不小于2的整数,r是任意非负整数,当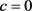 时,
时, 。当
。当 时,
时, ,当
,当 时这个等式是可以证明的,对猜想的证明可能会有帮助,当
时这个等式是可以证明的,对猜想的证明可能会有帮助,当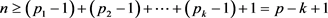 时,方程① 所有非负整数解中都存在不满足要求的值,此时
时,方程① 所有非负整数解中都存在不满足要求的值,此时 ,把
,把 代入此式就可以证明。当
代入此式就可以证明。当 和
和 时,也可以证明等式成立。
时,也可以证明等式成立。
4. 容斥原理证法分析和问题推广应用
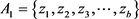 ,
, ,
,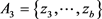 ,
, ,
, ,从b个集合中取m个集合的交集之和是
,从b个集合中取m个集合的交集之和是 ,m等于
,m等于 分别代入此式,
分别代入此式,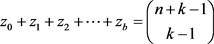 或
或 或其它的式子,从不定方程解的数量可知与本文b个等式类似的等式大量存在 [7] 。b个等式就是一组方程,其解是唯一的,组成的b个集合也是唯一的,b个集合的交集是多样的,现在容斥原理证明与本文类似的问题时,没有给出具体的集合 [6] ,交集特征的描述也比较单一 [6] ,对应的集合是否存在还有疑问。容斥原理证明的过程中
或其它的式子,从不定方程解的数量可知与本文b个等式类似的等式大量存在 [7] 。b个等式就是一组方程,其解是唯一的,组成的b个集合也是唯一的,b个集合的交集是多样的,现在容斥原理证明与本文类似的问题时,没有给出具体的集合 [6] ,交集特征的描述也比较单一 [6] ,对应的集合是否存在还有疑问。容斥原理证明的过程中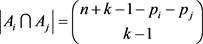 [6] ,本文的理论却是否定的,
[6] ,本文的理论却是否定的,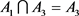 集合中不存在两个x值不满足要求的解,但是
集合中不存在两个x值不满足要求的解,但是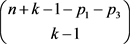 组不同的新解中却存在。交集之和一般都存在多个相同的元素,交集之和的值中是否对应存在还需证明,容斥原理没有这方面的证明 [6] 。
组不同的新解中却存在。交集之和一般都存在多个相同的元素,交集之和的值中是否对应存在还需证明,容斥原理没有这方面的证明 [6] 。
命题同样的方法可求出方程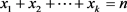 (
(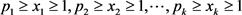 )的正整数解的数量。
)的正整数解的数量。
5. 结论
参考文献7用集合理论证明了类似的等式存在较多,根据此推出了这里的新等式和任意条件下可重复组合的计数公式,这是一种新证法,并指出了容斥原理证明此类问题的不足,因此本文具有一定的参考价值。
参考文献