1. 引言
在实际的振动主动控制系统中,为了消除误差通道对系统稳定性的影响,常常采用基于滤波x-LMS (FxLMS)算法 [1] 的自适应有源控制策略。与其他的算法相比,它具有结构简单、鲁棒性好、计算量小等优点 [2] [3] [4] 。FxLMS算法需要对误差通道进行在线辨识,并使用辨识得到的误差通道权向量对参考信号进行滤波。理论上说对误差通道辨识得越准确,它对控制系统的影响就越小,因而控制效果也越好 [5] 。常用的误差通道辨识方法可分为离线辨识和在线辨识两类。当被控系统的参数变化慢或近似不变时,采用误差通道离线辨识可使控制算法大大简化。然而在多数情况下系统误差通道是时变的,需要对误差通道进行在线辨识以保证滤波FxLMS算法收敛,因此对基于误差通道在线辨识的自适应控制算法的研究对于时变系统的振动控制具有重要的意义 [6] [7] 。
误差通道在线辨识按是否需要外加噪声可分为叠加噪声方法和整体考虑方法。前者需要在控制器输出端叠加噪声而后者直接利用控制信号本身进行误差通道在线辨识。研究表明 [8] [9] [10] ,叠加噪声的方法在收敛性、辨识环节与控制环节的独立性、对被控信号变化的响应速度以及计算的复杂程度等方面具有优越性,因此本文只对叠加噪声的在线辨识方法进行研究。
早在1989年,Eriksson [11] 就提出了一种通过在控制器输出端加入随机噪声信号实现误差通道在线辨识的方法。该方法的缺点在于其控制环节和辨识环节是相互影响的,这种影响严重时会导致系统不收敛,外加的随机噪声信号会对主动控制过程中控制滤波器权值的调整产生影响,导致误差信号中总是会有一定量级的残差。为了解决控制环节和辨识环节相互影响的问题,Bao [12] 、Kuo [13] 和张明 [14] 等人对Eriksson的方法进行了改进研究。其中张明等提出的控制策略是在系统中加入一个附加滤波器,很好地解决外加噪声对控制器权系数的影响以及控制环节和辨识环节的相互影响,但是与Eriksson的方法相比较,系统的复杂程度增加了,导致误差通道的建模速度降低,而且当误差信号收敛后其中还会含有与加入的随机噪声的功率大小呈比例关系的残差存在。为了消除随机噪声对误差信号造成的残差影响,H. Lan [15] 等人提出了一种的基于误差通道在线辨识的振动主动控制方法。该方法是在张明方法的基础之上改进得到的,通过将辨识环节输入的白噪声信号乘上动态系数控制其在控制阶段和即将收敛阶段不同的功率大小,解决了由输入白噪声信号功率所引起的矛盾。实验研究表明该方法的误差通道辨识效果不如张明方法的理想,但是却能得到较好的控制效果。在实际的应用中,我们要得到的就是系统具有良好的控制效果,因而该方法是具有优势的。
2. 本文提出的方法
对于H. Lan等人提出的变随机噪声的方法,前文提到它对于误差通道的辨识效果不如张明的方法。理论上来说,误差通道辨识的效果越好,控制环节的误差信号e(n)收敛时的量级就越小,于是本文在H. Lan的方法的基础上,结合Akhtar [16] 方法的辨识环节采用变步长因子的思想得到本文的方法,其原理框图如图1所示。与H. Lan的方法相比较,本文方法进一步提高了对误差通道的辨识效果,使得e(n)的残差得到进一步降低,控制效果更好。
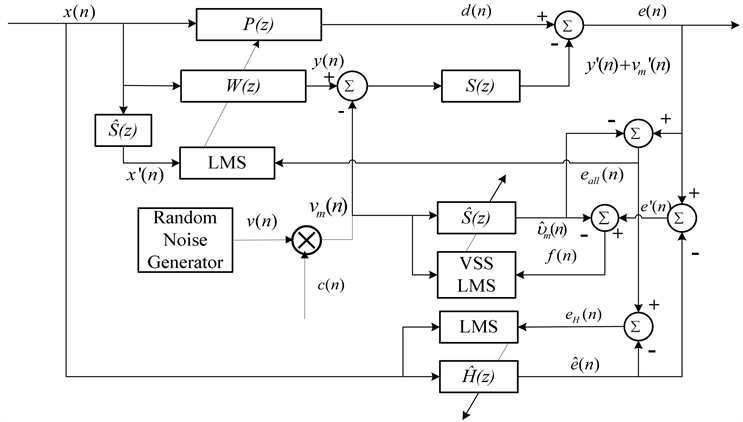
Figure 1. Systematic block diagram: the method presented in this paper
图1. 本文的方法的系统结构框图
本文提出的方法采用变步长的思想,使得误差通道的辨识速度随着子系统残差的强弱变化而变化,一方面提高了误差通道的辨识速度,另一方面当误差通道权系数收敛时,该方法同样能够大大减弱叠加白噪声对控制系统的影响。由框图可知,对于控制环节有:
(1)
(2)
(3)
(4)
其中,
表示前一时刻误差信号的绝对值。
为步长因子,L为控制滤波器
的阶数。
对于辨识环节有:
(5)
在系统控制进行的初始阶段,
具有较大的幅值,辨识环节的步长因子应取得较小,否则会导致辨识环节不稳定;当控制进行一段时间且控制环节趋于收敛时,
幅值较小,此时采用较大的步长因子加快对误差通道的辨识。为了实现辨识环节步长因子随着系统的进程不断发生改变采用Akhtar [16] 的变步长因子方法,具体步骤如下:
首先利用下式分别计算出控制环节和辨识环节的误差信号的功率
和
,
(6)
其中:
为遗忘因子,其取值范围为
,当
时,
,
则步长因子
可表示为:
(7)
其中:
,
,
定义为:
(8)
于是辨识滤波器的权向量迭代公式为:
(9)
3. 仿真及结果分析
将本文提出的方法在MATLAB环境下进行两种情况下的振动主动控制仿真,并与张明、H. Lan的方法进行比较,为了便于比较选取误差通道辨识结果
和真实误差通道
之间的相对误差
作为评定辨识效果的好坏,其表达式为:
(10)
主动控制环节控制效果由参数R(n)来衡量,其表达式为:
(11)
仿真中的系统的初级通道
和误差通道
是由文献 [1] 中提供的实验数据得到,可以把它们分别看作阶数为48和16的FIR滤波器,其频率响应曲线如图2中黑色实线所示。
在仿真过程中,选取控制滤波器
和附加滤波器
的阶数为32,辨识滤波器
阶数为16,采样频率
,滤波器的初始值均设为零。
仿真一:
仿真过程中,参考信号x(n)是由基频为50 Hz的四个正弦信号组成的,随机噪声信号采用方差为1的高斯白噪声信号。每种方法的参数的选取满足使控制系统具有最佳的效果,它们的值的选取如表1所示:
仿真的结果如图3所示,从图3(a)中可以看出,与H. Lan的方法相比,本文方法在误差通道辨识的精度上有所提高,但是依然没有张明的方法好;由图3(b)可知,本文的方法具有最快的收敛速度,收敛的效果也比较好,而且与其他两种方法相比具有最大的振动减少量(R)。图4是采用各种控制算法的控前和控后的振动信号的频谱比较图,不难发现本文的算法的减振效果比其它两种要好。
仿真二:
仿真中,参考信号x(n)和随机噪声信号v(n)的选取以及三种控制算法参数的取值都与仿真一中的相
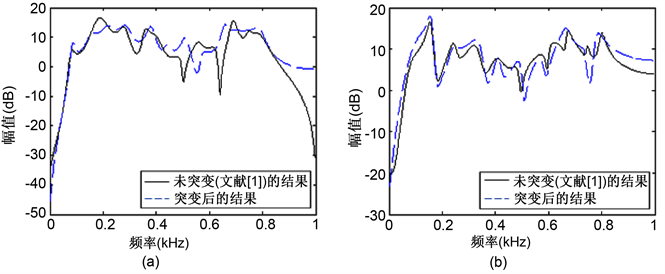
Figure 2. Frequency response of the controlled system. (a) The primary path; (b) The secondary path
图2. 被控系统的频率响应曲线。(a) 初级通道;(b) 误差通道
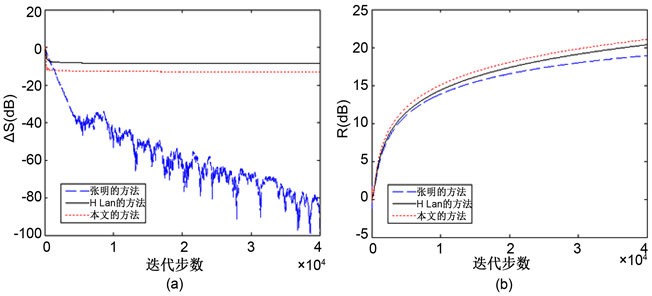
Figure 3. The simulation results of configuration one. (a) Relative error of secondary path modeling; (b) Vibration reduction
图3. 仿真一的仿真结果图。(a) 误差通道建模相对误差;(b) 振动减少量

Table 1. The parameters of three simulations
表1. 三种方法的仿真参数
同,但是在系统控制进行到迭代步数为n = 20,000时,系统的初级通道和误差通道发生突变,初始时刻和变化之后的初级通道和误差通道的频率响应曲线如图2所示,图中黑色实线和蓝色虚线分别表示初始时和突变之后的频率响应曲线。
仿真得到的系统控制效果对比和误差通道辨识的相对误差对比,分别如图5(a)和图5(b)所示。通过分析可以看出,当被控系统的误差通道发生变化时,系统并没有出现发散的现象,经过一段时间的调整后,系统的振动又重新收敛得到良好的控制。误差通道的辨识精度也较高,经历突变之后能再次实现较高的
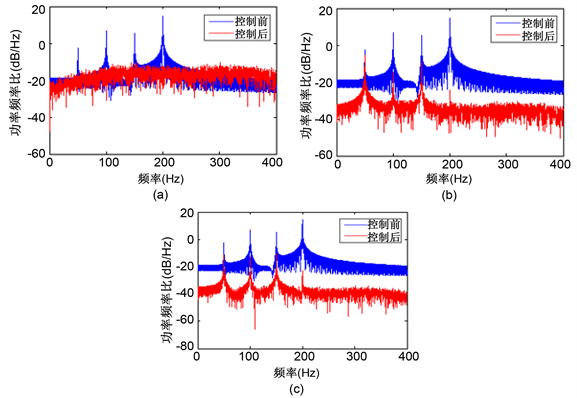
Figure 4. Comparison between three methods on vibration reduction. (a) The method of Zhang Ming; (b) The method of H. Lan; (c) The method of this paper
图4. 三种方法控制效果对比。(a) 张明的方法;(b) H. Lan的方法;(c) 本文的方法
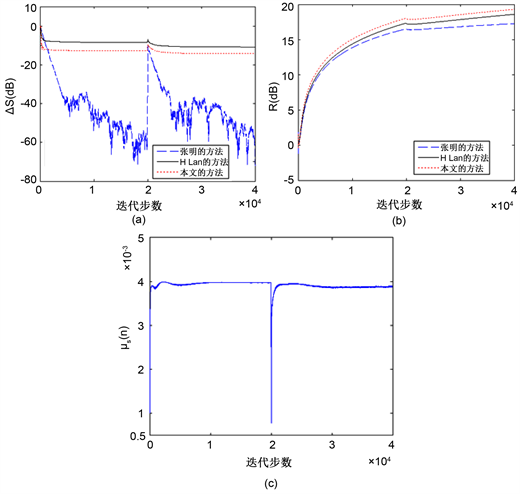
Figure 5. Simulation results of configuration two. (a) Relative error in secondary path modeling; (b) Vibration reduction; (c) The spectrum of vibration signal before and after control
图5. 仿真二的仿真结果图。(a) 误差通道建模相对误差;(b) 振动减少量;(c) 控前控后振动信号频谱
辨识精度,最终达到稳定值,且精度优于H. Lan的方法。因此,本文所用方法对系统参数的变化具有较强的适应性和鲁棒性。
4. 结论
在H. Lan的方法的基础上,结合Akhtar方法的变步长因子的思想,本文提出了一种新的具有误差通道在线辨识功能的自适应控制算法,该算法实现了控制环节和误差通道辨识环节的相互独立。仿真实验结果表明,在控制的收敛速度与算法稳定后的控制效果上,该算法都优于其它两种算法,而且当系统的初级通道和误差通道发生突变时,系统能进行很好地适应这种变化,具有更好的鲁棒性。