1. 引言
随着世界新兴经济体的涌现和全球格局的不断升华,世界各国在能源方面的需求不断增加,对诸如石油、煤炭、天然气等传统能源的争夺也日益加剧,作为常规资源的有效补给,页岩气已经受到全世界的广泛关注 [1]。研究表明,作为页岩气藏中储集的有效空间以及运移的主要通道,裂隙发育程度是控制页岩气成藏的主要因素之一,对页岩气产能起决定作用 [2]。另外,在对页岩气进行开采抽取时,页岩中天然裂隙的形态、走向及密集度等对水力压裂技术的有效发挥也有着重要的影响 [3]。因此,深刻理解含裂隙页岩的各项物理及力学特征对于页岩气产能评估及勘探开发尤为重要。
目前,国内外学者对含裂隙页岩有一定程度的研究。例如:ZHOU等 [4] 推导了含倾斜裂隙页岩介质等效弹性系数的计算公式,研究了裂隙页岩介质中波传播特征;魏元龙等 [5] 通过单轴循环加载的试验方法,对含天然裂隙脆性页岩的变形及破裂特征开展了试验研究;王怡 [6] 等借助泥浆化学等研究手段,对含裂缝泥页岩的理化及力学特性进行了分析;赵凯等 [7] 进行了不同角度下页岩的单轴压缩试验,研究了层理裂隙对水平井稳定性的影响;康志勤等 [8] 利用CT扫描技术对高温下的油页岩进行了微观观测和分析,探究了油页岩热破裂裂隙的规律;梁榜等 [9] 在调研总结国内外泥页岩研究成果的基础上,分析了泥页岩中裂隙的发育特征以及裂隙对含气性的影响;林永学等 [10] 采用多种手段评价和分析了龙马溪组页岩的强度,认为微裂隙对页岩整体强度具有决定性的影响;SP Morgan [11] 等对4组不同层理倾角页岩预设了裂隙缺陷,对其开展了单轴压缩试验以研究层理方向对缝隙扩展及交汇的影响;K. Sun等 [12] 通过三轴水力压裂测试系统对页岩水力压裂进程中天然层理方向对裂隙扩展的影响。以上研究大多集中于页岩裂隙的诱导扩展及气体在裂隙中的传输机制,对含裂隙页岩力学特性的基础研究却比较少见,考虑到裂隙在页岩气储存及开采中的重要作用,因此有必要开展含不同裂隙形态页岩的力学特性研究。
在借助室内试验研究含裂隙页岩力学特性时,采样及试件加工过程会对天然裂隙产生较大的扰动,且比较容易诱发次生裂隙 [10]。除此之外,天然裂隙与层理的位置关系比较复杂,室内试验的少量试样不足以体现裂隙的多样分布形式。针对以上室内试验研究的不足,本文尝试采用数值方法研究天然裂隙对层状页岩强度特性的影响。在数值研究过程中,首先通过页岩以及带裂隙模型材料的压缩试验数据验证Jointed Rock模型应用的可行性。然后利用Jointed Rock模型建立典型的含裂隙页岩数值模型,并结合室内试验所得的力学及物理参数初步研究不同天然裂隙形态对页岩强度特性的影响。
2. 不同层理倾角下页岩压缩试验
所研究的页岩取自重庆彭水境内。现场用钢钎等工具选取规整形状的新鲜页岩露头,然后将其小心移入室内进行钻样,首先钻取直径为50 mm,层理倾角为β = 0˚,60˚及90˚ (如图1所示,规定β为钻进方向的法向与层理方向所成角度)的圆柱,然后将圆柱加工为高为100 mm,端面平行度上下限为±0.02 mm,误差上下限为±0.05 mm的标准圆柱试样。压缩试验通过四川大学MTS815 Flex Test GT岩石力学试验系统来完成,该系统为全数字计算机自动控制系统,轴向可加载至4600 kN,轴向位移±50 mm,轴向引伸计±4 mm,环向引伸计−2.5~12.5 mm,可实时记录荷载、应力、位移和应变值,并同步绘制荷载-位移、应力-应变曲线。试验采用由LVDT调节的轴向位移控制方式,加载速率为0.05 mm/min。
试验前对加工好的试件进行编号记录,同时测得页岩的平均密度为2650 kg/m3。分别对各倾角下加工好的试件进行单轴压缩试验以及4种不同围压下的三轴压缩试验,每种围压状态取3个试件,最后计算3个试件平均值,并以此代表该倾角及围压状态下的试验结果(表1)。

Table 1. Mechanical parameters of different angles of the shale foliation
表1. 不同层理角度下页岩的力学参数

Figure 1. The definition of angle of foliation
图1. 试件层理倾角定义
对破坏后的试件观察发现,相同层理倾角试件在各围压下压缩破坏后的形态比较一致,如图2所示。层理倾角为0˚时,试件主要发生贯穿基质的剪切破坏;层理倾角为60˚时,试件发生沿层理的滑移破坏;层理倾角为90˚时,试件发生沿层理的张拉劈裂破坏,另外0˚及90˚都出现了共轭的破坏面。

Figure 2. Typical failure modes of different angles of shale foliation
图2. 不同页理倾角页岩典型破坏形式
Tien和Kuo等 [13] [14] 借助层状岩石三轴试验数据给出了岩石弱面和基质的强度抗剪参数。同样,鉴于试件破坏形式,可以认为0˚、60˚试件的破坏分别受基质及层理的剪切强度控制。如图3,分别对0˚、60˚三轴压缩的抗压强度试验值进行线性拟合。

Figure 3. Shale matrix and bedding strength parameters fitting
图3. 页岩基质及页理强度参数拟合
基质的剪切强度参数:
(1)
(2)
层理剪切强度参数:
(3)
(4)
其中,
及
分别表示基质(层理)的摩擦角及基质(层理)的粘聚力;
和
分别表示围压
下0˚、60˚试件抗压强度。
3. Jointed Rock模型应用验证
Jointed Rock模型考虑了含弱面岩体非均匀力学特性效应,该模型将含弱面岩体等价为各向同性岩石与各向异性面的组合,弱面的破坏特征由带拉伸判据的各向异性Mohr-Coulomb准则决定。在ANSYS17.0中,弱面位置是通过其法向向量w来定义的。假设最初弱面局部坐标系(u, v, w)与整体坐标系(x, y, z)吻合,首先将弱面沿z轴旋转角度α,然后将弱面以当前坐标系下的v轴旋转γ,弱面经过上述2次旋转可表示实际岩石中任意位置,而旋转之后弱面的法线方向为,
(5)
ANSYS17.0中的Jointed Rock模型并不要求在试件的几何模型上对层理和基质进行区分,而是在定义材料非线性力学特征的过程中独立设置两者的强度参数等信息 [15]。该模型将页岩视为一种均匀各向异性材料,不体现层理具体空间位置及厚度。层理及裂隙常常都被当作力学特性较弱的结构面统一对待,事实上两者有一定区别:层理与基质的区分主要表现在矿物的成分及排布方式上的差异,两者方向一致交互叠加;而天然裂隙与基质(层理)具有明显的分界线,裂隙宽度0.6~2 mm,方向随机 [16]。因此有必要分别对Jointed Rock模型在层理及裂隙岩石上的适用性加以验证。
3.1. Jointed Rock模型在裂隙岩体中的应用验证
Ghazvinian等 [17] 人开展了预制裂隙面的物理模型材料试验,得到了多种工况下试件的抗压强度值。文献 [17] 中无裂隙试件的弹性模量及泊松比分别为1.43 GPa和0.31;无裂隙试件的粘结力及摩擦角分别为1.6 MPa和39.5˚。对4组不同形态的含裂隙试件进行了6种不同围压(0.5 MPa,1 MPa等)下的压缩试验,研究结果表明,当裂隙倾角θ为0˚时试件发生剪切及劈裂破坏,30˚时试件发生裂隙滑移破坏,15˚及45˚时发生劈裂及扭转破坏。
在文献 [17] 研究成果的基础上选择具有代表性破坏模式的试件(0˚,15˚,30˚)进行数值计算,试验数据见表2所示。

Table 2. Compressive strength of different fracture angles under different confining pressures in Ref. [17]
表2. 文献 [17] 中各围压下不同裂隙倾角抗压强度
同样,裂隙面的强度参数(摩擦角 粘聚力)通过表2中30˚试验值的线性拟合得到。
根据层理与裂隙关系可得如下关系式
(6)
于是,裂隙面的摩擦角
及粘聚力
分别为:
(7)
借助ANSYS17.0 Jointed Rock模型建立3种不同裂隙面倾角θ的试件模型,其中,基质的强度参数与无裂隙试件相同,裂隙面Joint1及Joint2的强度参数取为式(7),两者位置由下式决定,
(8)
其中, 依次取值0˚,15˚,30˚。鉴于石膏的力学特性,取基质与裂隙的张拉强度近似为0,各工况下的数值解列于表3。

Table 3. Numerical solution of different confining pressures (/MPa) in Ref. [17]
表3. 文献 [17] 中各裂隙倾角下不同围压的数值解(/MPa)
对比表2~3发现,大部分试验值与数值解的偏差率小于5%,证明Jointed Rock模型对含裂隙岩石的数值计算是合理的。
3.2. Jointed Rock模型在无裂隙页岩中的应用验证
压缩试验的整个数值模型由底部压头、试件及顶部压头3部分构成,试件与压头的高度/直径分别为2和0.5,且压头直径为试件直径的2倍。定义2组接触对来考虑试件与压头上下之间的接触关系,同时分别选取Contact170、174作为目标面单元和接触面单元,并将170单元摩擦系数设置为0。加载前需要约束底部压头位移的(X、Y、Z)向,试件位移的(X、Y)向以及顶部压头位移的(X、Y)向。本文是通过控制顶部压头上表面向下的位移进行加载的,对于三轴压缩试验而言,大小为CofPres的围压需要通过2步完成施加:首先于试件外壁施加大小为CofPres的围压,然后于顶部压头上表面施加大小CofPres/4的围压(压头横截面积为试件横截面积的4倍)。
第2节页岩压缩试验给出了基质及层理的剪切强度参数,由文献 [18] 可得相应的张拉强度,各参数取值见表5。将数值计算结果及偏差率列于表4。由表4可得,除60˚单轴压缩对应的值偏大以外,其余数值解均与试验值比较接近。因此,Jointed Rock模型对层状页岩抗压强度的计算是成功的。

Table 4. Numerical solution (MPa) and deviation (%) of shale compressive strength
表4. 页岩抗压强度数值解(/MPa)及偏差率(%)
综上所述,针对其他学者模型试验以及本文进行的页岩压缩试验,利用Jointed Rock模型分别对预制裂隙及天然层理两种不同机理的弱面进行模拟,计算发现试验值与数值解均有较好的吻合度,因此Jointed Rock模型对含裂隙层状类岩石抗压强度的数值计算是可行的。
4. 不同裂隙倾角下页岩抗压强度的数值计算
如图4所示,为了体现裂隙与层理关系的多样性,设置3类共21组具有代表性的含裂隙页岩试件:在层理倾角
试件下分别引入7组不同倾角的裂隙面,倾角θ介于0˚~90˚,梯度为15˚。
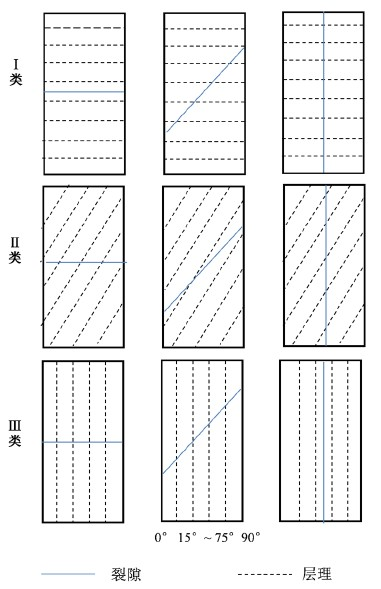
Figure 4. Typical configurations of bedding and fracture
图4. 层理及裂隙面代表性构型
模型建立时所使用的基质、层理及裂隙面的强度参数见表5:采用Joint1模拟层理,Joint2模拟裂隙面,膨胀角及各残余强度值均是根据工程经验给出的。在与室内压缩试验对照的情况下,选用6级围压(0,10 MPa,20 MPa等)对各数值模型进行计算,计算工况为126种。需要说明的是,与室内试验相比,数值试验增设了20 MPa围压,其目的在于更合理归纳数值试验结果的规律。

Table 5. Numerical simulation of the strength parameters
表5. 数值模拟所需强度参数
引进一个无量纲量Ae来表征倾角为β的裂隙对页岩强度的影响,Ae的大小直接反应裂隙对页岩压缩强度削弱的强弱。
(9)
其中,
为层理倾角为β的无裂隙页岩抗压强度,0˚,60˚,90˚层理倾角对应20 MPa围压下的抗压强度值分别为183.05,165.79,187.95 (MPa),其余数值解见表4;
为层理倾角为β、裂隙倾角为θ的页岩抗压强度。计算各工况下的Ae值将其列于表6、表7和表8。

Table 6. Ae (%) of Class I model under different calculation conditions
表6. 不同计算工况下I类模型Ae(%)

Table 7. Ae (%) of Class II model under different calculation conditions
表7. 不同计算工况下II类模型Ae(%)

Table 8. Ae (%) of Class III model under different calculation conditions
表8. 不同计算工况下III类模型Ae(%)
对表6中I类模型的数值计算结果进行分析可知,裂隙的存在对页岩的抗压强度有一定程度的影响,由于裂隙强度参数较低,试件整体抗压强度被削弱。不同倾角裂隙对页岩抗压强度的削弱程度不一:0˚,15˚,90˚的Ae值接近0,其他倾角下Ae从大到小依次为60˚ > 45˚ > 75˚ > 30˚。
从数值模型结果可知,裂隙角为45˚,60˚,75˚时,应变在裂隙方向局部化明显,试件沿裂隙方向发生滑移破坏;这与相同弱面倾角下其他层状类岩石的破坏模式类似 [19]。
随着围压的增大,相同裂隙倾角下的Ae逐渐减小,这是由于围压下试件沿裂隙面的滑移破坏受到抑制,裂隙对页岩抗压强度影响逐渐减弱。
已知
呈负相关,与
呈正相关。引入比率
,并分析30˚,45˚,60˚,75˚裂隙倾角下该比率与Ae的关系,如图5,Ae与
关系近似线性,且除30˚外,线性关系的斜率趋于一致。从图中也可以看出,
为零,即单轴压缩时Ae最大,裂隙对抗压强度影响最大。
Ae随裂隙倾角θ的增大呈现先增后减的趋势,并在θ = 45˚~60˚内取得最大值,将表6中数据进行拟合得图6。

Figure 5. The relationship between Aeand
in model I
图5. I类模型Ae与
的关系

Figure 6. The relationship between Aeand θ in model I
图6. I类模型Ae与θ的关系
以
和θ为变量对Ae进行拟合,得到拟合关系式为式(10),其调和确定系数
。
(10)
其中 以弧度制表示。对所有取值的裂隙倾角有:
(11)
令:
(12)
有:
(13)
因此,同围压下裂隙倾角为56.56˚时,裂隙对I类模型抗压强度影响最大。
同理,对表7、表8中数据进行分析,可以发现II、III类模型数值计算结果与I类模型有近似的结果。当θ为0˚,15˚,90˚时,Ae近似为0;其他角度下Ae与
和θ的拟合关系的形式为式(14),将3类不同计算模型拟合关系的参数结果列于表9,不同模型拟合公式中的参数a、b、c和d大体相当,各模型的Ae在57˚左右取得最大值。
(14)
比较表6、表7和表8相同围压条件下裂隙倾角30˚,45˚,60˚,75˚的Ae发现,I、III类模型Ae比较接近,而II类模型Ae比I、III类小。本文认为裂隙引入与否Ⅱ类模型均易于发生层理(裂隙)主导的滑移破坏,强度差异较小;对于I、III类模型而言,随着裂隙的引入,破坏的主导因素由基质转向层理(裂隙),强度差异较大。

Table 9. Summary of 3 kinds of model fitting parameter Ae
表9. 3类不同模型Ae拟合参数汇总
5. 结论
基于页岩压缩试验和其他学者研究资料,验证了数值计算手段的可行性。通过对多种工况下数值模型的计算研究了不同裂隙形态对页岩抗压强度的影响,最终得到以下结论:
(1) 室内试验难以对裂隙页岩进行系统研究,借助ANSYS17.0 Jointed Rock模型可以对多种分布裂隙的页岩试件进行分析,具有明显的优势。
(2) 裂隙对不同层理倾角页岩抗压强度的影响趋势一致,57˚左右的裂隙倾角对页岩抗压强度的削弱程度最明显,之后向两边递减,在0˚,15˚,90˚时裂隙对页岩抗压强度基本不存在影响。
(3) 相同条件下,裂隙对60˚页岩的抗压强度影响较小,对0˚、90˚页岩的抗压强度影响较大,而这主要与裂隙页岩的破坏形式有关。
(4) 围压越高,围箍效应越明显,裂隙页岩抗压强度越大。另外,较高围压下试件沿裂隙方向的剪切滑移破坏难于发生,从而表现为裂隙对页岩抗压强度的影响作用(Ae)削弱。
NOTES
*第一作者。
#通讯作者。