1. 引言
细纱机主要是把粗纱制成细纱的纺纱机器,其中的牵伸机构主要由传动轴、基座、齿轮等结构组成。由于提高生产效率的需要,产量逐渐提高,齿轮作为动力传动的主要元件,其所受的载荷越来越大,以至出现齿轮破坏、传动轴扭转振动等问题 [1] [2] [3] ,因此,需要分析现有齿轮受力状态、变形情况,为牵伸机构的合理使用和设计提供依据和参考。
由于牵伸机构是一个复杂的系统,在动力传递过程中,各个传动轴都会发生弯曲变形,且轴承连接处并非是刚性连接,也存在一定弹性变形,利用传统的方法难以得出理想的计算结果,针对复杂系统的受力计算,国内外学者大都使用数值计算、有限元等方法,如:谢飞等人 [4] 在对直齿圆锥齿轮进行三维参数化设计的基础上,利用CATIA进行有限元分析,校核结构强度;王建军等人 [5] [6] [7] 研究了齿轮—转子系统的动态特性,并对斜齿轮进行轮廓修形;唐进元等人 [8] [9] [10] 主要对齿轮的啮合刚度和啮合特性进行了深入研究。叶友东等人 [11] 分析了直齿圆柱齿轮的各阶模态以及各阶振型;周驰等人 [12] 利用ABAQUS对准双曲面齿轮的啮合点、啮合力大小、啮合力方向等参数进行了深入研究,并对比了有限元计算的传动误差曲线。柴欢等人 [13] 利用ANSYS/Ls-dyna软件对船用齿轮箱斜齿轮进行了接触分析,准确的计算出齿轮Mises应力集中区域,并验证齿轮最大Mises应力小于材料强度极限,满足工程需求。
本文基于有限单元法对牵伸机构进行分析,计算齿轮的应力状态,分析齿轮发生破坏的原因,并进行结构优化,为牵伸机构的设计与使用提供理论指导。
2. 牵伸机构计算模型的建立
2.1. 计算模型
图1为牵伸机构三维模型图,包括底座、前轴、中间轴、后轴、齿轮等,牵伸机构主要用于传递动力和运动,前轴和后轴同速转动;输入的扭矩为200 Nm,扭矩在前轴的左端输入,即图1中扭矩输入端;扭矩主要在后轴右端输出,即图1中扭矩输出端;中间轴主要用来传递运动,其右侧的外伸端输出扭矩较小忽略不计。前轴、中间轴和后轴之间由两组齿轮完成传递,齿轮参数如表1所示,其中齿轮1和齿轮2为降速,齿轮3和齿轮4为增速,且降速比与增速比相同,从而保证前轴和后轴具有相同的转速。
齿轮材质为16MnCr5,其弹性模量为2.1 × 105 MPa、泊松比为0.3,屈服强度为635 MPa;前轴、后轴和中间轴为45号钢,其弹性模量2.1 × 105 MPa、泊松比为0.27,基座材料为铸件,其弹性模量1.6 × 105 MPa、泊松比为0.25,由于产量的提升,传递扭矩为200 Nm时,导致齿轮3发生破坏。
齿轮1安装在前轴上,齿轮4安装在后轴上,齿2和齿轮3安装中间轴上;由图1可知,齿轮1、齿轮2和齿轮4是两端支撑,而齿轮3则安装在中间轴的外伸段上。表1为四个齿轮的设计参数。
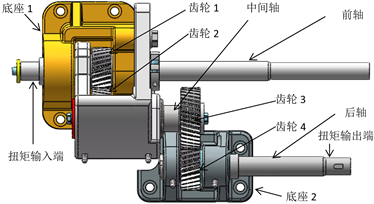
Figure 1. Three-dimensional model of the drafting mechanism
图1. 牵伸机构三维模型图
2.2. 牵伸机构边界条件
底座1通过四个螺栓连接在细纱机上,底座2通过三个螺栓连接在细纱机上,螺栓孔处设置为固定;前轴、后轴和中间轴通过轴承与底座连接在一起,将轴承连接处设置为铰接;齿轮1与齿轮2、齿轮3和齿轮4之间设置为接触连接;扭矩输入端设置为200 Nm扭矩输入,而扭矩输出端设置为周向位移约束。
3. 计算结果分析
图2为扭矩在200 Nm时,齿轮1、齿轮2、齿轮3和齿轮4的Mises应力分布图,从图2可知:齿轮1的最大Mises应力为558.38 MPa,齿轮2的最大Mises应力为571.74 MPa,齿轮1和齿轮2的Mises应力非常接近,且最大Mises应力均小于16MnCr5的屈服强度;齿轮3的最大Mises应力为752.43 MPa,大于16MnCr5的屈服强度,因此该齿轮最容易发生破;齿轮4的最大Mises应力为611.29 MPa,小于16MnCr5的屈服强度,但也比较接近屈服强度。四个齿轮的Mises应力均表现为左侧大右侧小的分布规律,其原因为:齿轮1左侧靠近扭矩输入端,使齿轮1和齿轮2的左侧啮合更加紧密,而齿轮3由于安装在中间轴的外伸段,导致齿轮3产生一定的偏转,致使齿轮3和齿轮4左侧啮合较好、右侧啮合较差所致。
 (a) 齿轮1
(a) 齿轮1  (b) 齿轮2
(b) 齿轮2 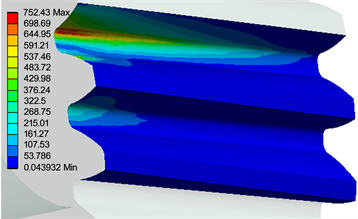 (c) 齿轮3
(c) 齿轮3  (d) 齿轮4
(d) 齿轮4
Figure 2. Gear stress distribution
图2. 齿轮应力分布图
图3为齿轮1、齿轮2、齿轮3和齿轮4最大Mises应力曲线图,从图3中可以,齿轮3最大Mises应力最大、其次是齿轮4,齿轮2和齿轮1,其中齿轮1和齿轮2最大Mises应力较小。牵伸机构在实际运行中,齿轮3经常发生破坏,具体破坏图片,如图4所示,齿轮3发生破坏的区域主要集中在一侧,这主要是由于齿轮3安装在中间轴的外伸端,外伸端弯曲刚度较弱,导致齿轮3发生较大偏转角度所致。
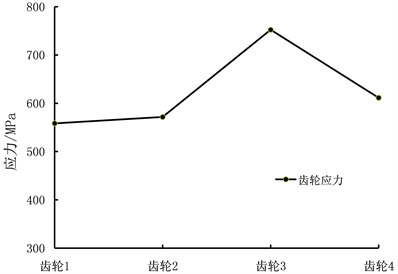
Figure 3. The maximum Mises stress curve of the gear
图3. 齿轮最大Mises应力曲线图
图5为中间轴转角变化曲线图,通过研究中间轴的转角变化曲线,进一步研究齿轮3破坏的原因。从图5看出:中间轴的转角自左至右,先逐渐减小后逐渐增大,在中间处转角最小,左端最大转角为0.0015 rad,右端最大转角为0.0025 rad。在中间轴110 mm~145 mm之间,中间轴的转角快速增大,这主要原因在中间轴属于悬臂梁结构,抗弯刚度较差,而齿轮3安装在中间轴的外伸段,导致齿轮3发生较大的偏转角,达到0.0025 rad,以至于齿轮3和齿轮4产生较大的Mises应力。而齿轮1和齿轮2由于均属于两端支撑,抗弯刚度较大,偏转角较小,所以齿轮1和齿轮2的Mises应力较小。
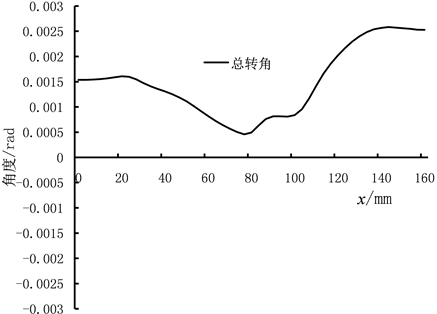
Figure 5. The curve of the intermediate shaft angle change
图5. 中间轴转角变化曲线图
4. 结构优化
根据分析,中间轴外伸端的弯曲刚度过低是造成齿轮3产生较大偏转角,引起齿轮3的Mises应力较大的主要原因,为了减小齿轮3的Mises应力,对中间轴结构进行优化,以增大中间轴的弯曲强度。根据材料力学弯曲变形中弯矩与曲率间的公式:
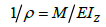 (1)
(1)
其中,
为曲率半径、M为弯矩,E为弹性模量。
(2)
EIz称为抗弯刚度,EIz越大,则曲率越小,转角也就越小。抗弯刚度EIz与直径d成4次方的关系,所以通过改变中间轴的直径是最有效的方案。中间轴蓝色区域直径由30 mm修改为35 mm,如图6所示。

Figure 6. The intermediate shaft structure modification diagram
图6. 中间轴结构修改图
图7为优化前后的应力对比图,显示了齿轮1、齿轮2、齿轮3和齿轮4优化前、后的应力变化曲线。从图7可以看出:通过改进中间轴的结构,四个齿轮的最大Mises应力均发生较大幅度的减小,齿轮3的Mises应力由752.43 MPa降低为579.2 MPa,降幅达23.02%,齿轮4的Mises应力由611.29 MPa降低为522.05 MPa,降幅达14.6%;齿轮1和齿轮2的Mises应力也发生了显著的降低,具体数值见表2。
图8为中间轴转角对比图,从图8可以看出:中间轴转角先逐渐减小后逐渐增大;左端的转角由优化前的0.0015 rad降低为0.0005 rad,右侧最大转角由0.0025 rad降低为0.0012 rad,中间轴转角明显减小。中间轴弯曲刚度的增大,减小了齿轮3的偏转角,使齿轮3和齿轮4接触面积增大,降低了齿轮3和齿轮4的Mises应力,同时,也降低了齿轮1和齿轮2的Mises应力。
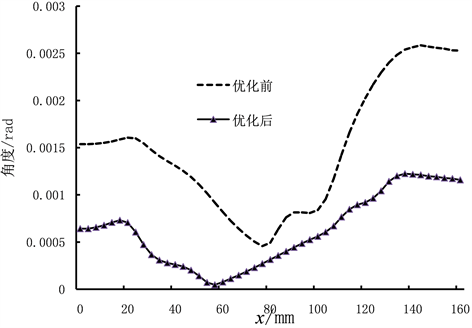
Figure 8. The comparison of the intermediate shaft angle
图8. 中间轴转角对比图
5. 结论
通过对牵伸机构分析,得出以下结论:
1) 四个齿轮的左侧Mises应力均大于右侧,其中齿轮1和齿轮2主要是因为左侧为扭矩输入端所致,而齿轮3和齿轮4主要是由于齿轮3安装在中间轴的外伸段上,致使中间轴产生较大的偏转角,从而引起齿轮3和齿轮4左侧Mises应力大于右侧Mises应力。
2) 由于中间轴属于悬臂梁结构,齿轮3安装在外伸段上,导致齿轮3的Mises应力较大,发生破坏。
3) 通过对牵伸结构的优化,降低了中间轴转角,增大了中间轴弯曲刚度,大大降低了齿轮3和齿轮4的Mises应力。
基金项目
上海市高峰高原学科(No. A1-5701-18-007-03);上海市自然科学基金资助(No. 15ZR1417200);国家高技术研究发展计划(No. 2012AA040106)。