1. 引言
在自然界中,种群之间的互惠关系是非常普遍的,如传粉昆虫与开花植物、豆科植物与根瘤菌、海葵与小丑鱼等。许多学者对互惠种群模型进行了深入研究,并获得了丰富的研究成果 [1] [2] [3] [4] 。而现实世界中,种群的演化不可避免地受到环境噪声的影响,而且这些噪声是不容忽视的,更合理的种群模型应包括随机因素 [5] - [11] 。近年来,随机互惠模型受到学术界的广泛关注 [11] - [21] 。
2006年,Gravesa等人 [3] 提出以下互惠模型
(1.1)
其中
是第i个种群在时刻t的种群密度;
为正常数,相应的生物意义见文献 [3] 。2009年,向等人 [4] 在系统(1.1)的基础上,考虑以下非自治互惠模型
(1.2)
建立了系统(1.2)的持续性、周期解的存在性和全局吸引性。2011年,为探讨随机扰动对系统(1.1)的影响,吕 [11] 考虑以下随机互惠模型
(1.3)
给出了系统(1.3)的持续性、灭绝性和全局吸引性。
本文在文献 [3] [4] [11] 基础上,研究以下具有随机干扰的非自治互惠模型
(1.4)
其中对
是连续函数,具有正的上、下界;
是定义在完备概率空间
上的二维标准Brown运动。本文旨在利用随机微分方程理论 [22] [23] [24] [25] ,探讨系统(1.4)的全局正解的存在唯一性、持续性、灭绝性、全局吸引性和周期解的存在性。
为方便讨论,给出以下记号:
1)
;
2) 对
上的有界函数f,定义
;
3) 给定
,对
上的可积函数g,定义
。
2. 正解的存在唯一性
本节建立系统(1.4)的全局正解的存在唯一性,这是本文后续工作的基础。
定理2.1:对任意初值
,系统(1.4)存在唯一的全局解
,并且该解以概率1停留在
中。
证明:易知系统(1.4)的系数满足局部Lipschitz条件。因此,对于任意初值
,系统(1.4)在区间
上存在唯一的局部解
,其中
是爆破时刻。下面证明
是全局的,即证明
几乎必然成立。取充分大的正整数
,使
和
。对任意正整数
,定义停时:
对于空集
,规定
。易知
是一个单调递增序列。令
,此时
,若证明
,则
。
下面用反证法证明
几乎必然成立。若该结论不成立,则存在常数
和
使得
.
从而,存在正整数
,使得对任意正整数
,有
.(2.1)
定义Lyapunov函数:
显然,对任意
,
。由Itô公式 [22] 得
(2.2)
其中
(2.3)
显然,
在
上有正的上界,记为M。
对(2.2)两边从0到
积分,然后取数学期望,再结合(2.3)得
(2.4)
对
,记
。由
的定义可知,对每个
,存在
的某个分量
等于m或者1/m。结合(2.1),有
(2.5)
其中
是
的示性函数。由(2.4)和(2.5)得
令
,有
矛盾。所以必有
。证毕。
3. 全局吸引性
本节讨论系统(1.4)的解得全局吸引性。为此,需要下面三个引理。
引理3.1:( [22] )如果
上的实值随机过程
满足
其中
、
和c均为正常数,那么存在
的一个连续修正
,使得对于任意的
,存在正随机变量
满足
换言之,
几乎所有的样本轨道都以指数
局部但一致Hölder连续。
引理3.2:( [26] )若非负函数
在
一致连续且可积,则
。
引理3.3:对于任意初值
,系统(1.4)的解
几乎所有的样本轨道都是一致Hölder连续的。
证明:对任意
,定义Lyapunov函数:
。由Itô公式得
(3.1)
令
。易知
在上
有正上界,记为
。对(3.1)两边从0到t积分,并取数学期望得
从而,
于是,存在与p和
有关的正常数
,使得对任意
,有
(3.2)
考虑系统(1.4)的第一个方程的随机积分形式:
(3.3)
其中
利用均值不等式,由(3.2)得
(3.4)
以及
(3.5)
对任意
和
,利用随机积分的矩不等式 [23] ,由(3.5)得
(3.6)
令
利用Hölder不等式,由(3.4)得
(3.7)
由(3.3)、(3.6)和(3.7)得
由引理3.1,对任意
时,
的几乎所有的样本轨道关于指数
是一致Hölder连续的。对
,同理可证。证毕。
下面给出系统(1.4)的解的全局吸引性结果。
定理3.1:若
,则对任意初值
,系统(1.4)的解
是全局吸引的。
证明:记
则
。设
和
分别系统(1.4)的初值为
和
的两个解,由Itô公式和Lagrange中值定理,可得
(3.8)
(3.9)
其中
位于
和
之间,而
位于
和
之间。令
利用Tanaka-Meyer公式 [22] ,由(3.9)得
即
于是,
在上
可积。另一方面,由引理3.3,
在
上一致连续。由引理3.2可知
从而,对任意初值
,系统(1.4)的解
是全局吸引的。证毕。
4. 持续性与灭绝性
本节讨论系统(1.4)的持续性与灭绝性。为此,介绍如下非自治随机Logistic方程的持续性结果。
考虑非自治随机Logistic方程
(4.1)
其中
、
和
连续,具有正的上、下界。对方程(4.1),由文献 [8] 可知:
引理4.1:若
,则方程(4.1)是随机持续的,即对任意
,存在正数
和
,使得对任意初值
,方程(4.1)的解
满足
引理4.2:若
,则方程(4.1)是平均持续的,即对任意初值
,方程(4.1)的解
以概率1满足
下面依次给出系统(1.4)的随机持续性、平均持续性和灭绝性结果。
定理4.1:若
,则系统(1.4)是随机持续的,即对任意
,存在正数
和
,使得对任意初值
,系统(1.4)的解
满足
证明:由定理3.1知,对于任意初值
,系统(1.4)存在全局唯一解,且以概率1停留在
中。对系统(1.4)的第一个方程,有
(4.2)
以及
(4.3)
考虑随机微分方程
(4.4)
和
(4.5)
设
和
分别是方程(4.4)和(4.5)的初值为
和
的解。根据随机微分方程的比较定理 [22] ,由(4.2)和(4.3)得
(4.6)
由引理4.1,当
时,系统(4.4)和(4.5)都是随机持续的。因此,对任意
,存在正数
和
,对任意
,有
和
(4.7)
由(4.6)和(4.7)得
和
(4.8)
同理可证,对任意
,存在正数
和
,对任意
,有
和
(4.9)
取
和
,由(4.8)和(4.9)可知,对任意
,有
证毕。
定理4.2:若
,则系统(1.4)是平均持续的,即对任意初值
,系统(1.4)的解
以概率1满足
证明:根据引理4.2,由
可知,对方程(4.5)的初值为
的解
,以概率1成立
(4.10)
由(4.6)和(4.10)可知,以概率1成立
同理可证,以概率1成立
证毕。
定理4.3:若
,则对任意初值
,系统(1.4)的第i个种群以概率1指数灭绝,即以概率1成立
证明:只对
的情况证明,
的情况类似。由Itô公式得
(4.11)
对(4.11)两边从0到t积分得
(4.12)
其中
是局部鞅,其二次变差为
由局部鞅的强大数定律 [23]
(4.13)
由(4.12)和(4.13)得
证毕。
5. 周期解
本节假定系统(1.4)的系数都是
-周期的。下面介绍Khasminskii [24] 的随机周期解理论,并据此建立系统(1.4)的
-周期解的存在性。
定义5.1:随机过程
称为是
-周期的,如果对任意有限个非负实数
,随机向量
的联合分布与
无关。
考虑随机微分方程
(5.1)
其中
,
。给定函数
,定义算子
引理5.1:( [24] )设
和
关于t是
-周期的。若方程(5.1)有全局唯一解,并且存在关于t是
-周期的函数
,使得:
1)
;
2)
;
则方程(5.1)存在一个
-周期解。
定理5.1:若
,则系统(1.4)存在一个正的
-周期解。
证明:由定理2.1,对于任意初值
,系统(1.4)存在唯一的全局正解
。令
利用Itô公式,由(1.4)得
(5.2)
定义Lyapunov函数:
,
,
其中
是微分方程
(5.3)
的初值为
的解,而q是满足
(5.4)
的充分小的正常数。对(5.3)两边从t到
积分得
于是,
是
-周期函数。显然,
即
满足引理5.1的条件(1)。由(5.3)和(5.4)得
同理,
于是,
(5.5)
由(5.4)和(5.5),易知
,
即
满足引理5.1的条件(2)。于是,系统(5.2)存在一个
-周期解。从而,系统(1.4)存在一个正的
-周期解。证毕。
6. 数值模拟
为验证理论分析结果,本节采用Milstein方法 [25] 对随机系统(1.4)进行数值模拟。
例6.1 在系统(1.4)中,取
,
,
,
,
,
,
,
,
,
,则
满足定理4.1的条件。从图1可知系统(1.4)是随机持续的。
例6.2在系统(1.4)中,取
,
,
,
,
,
,
,
,
,
,则
满足定理4.3的条件。从图2可知系统(1.4)的种群1是随机持续的,但种群2是灭绝的。
例6.3在系统(1.4)中,取
,
,
,
,
,
,
,
,
,
,则
满足定理3.1和定理5.1的条件。从图3可知系统(1.4)存在唯一的全局吸引的
-周期正解。
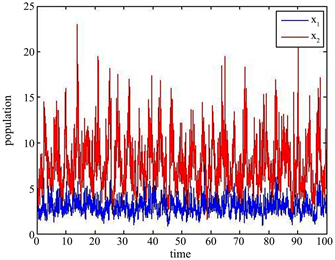
Figure 1. A solution of example 6.1 with initial value
图 1. 例6.1的初值为
的解
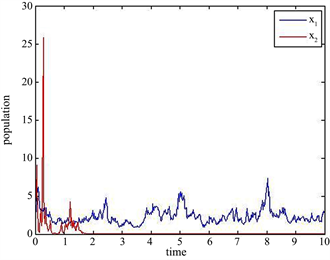
Figure 2. A solution of example 6.2 with initial value
图2. 例6.2的初值为
的解

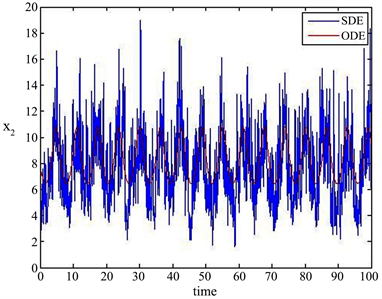
Figure 3. Solutions of example 6.3 and its determined counterpart with initial value
图3. 例6.3及其对应确定性方程的初值为
的解
基金项目
本文得到国家自然科学基金项目(11271110)和河南省教育厅科技攻关项目(15A120009)的支持。
NOTES
*通讯作者。