1. 引言
1978年,Hochstadt与Lieberman [1] 证明了如下著名的Hochstadt-Lieberman唯一性定理:
定理1.1 对于定义在[0, 1]区间上的Sturm-Liouville算子
:
(1)
满足Dirichlet-Dirichlet (DD)边值条件:
,(2)
其中
为实值函数,若q在子区间
上已知,则一组Dirichlet-Dirichlet特征值
唯一确定
区间上的势函数q。
Martinyuk及Pivoarchik [2] 曾对以上唯一性定理给出了重构势函数的方法。本文的目的是对Hochstadt-Lieberman唯一性定理提供一种新的重构势函数的方法。通过应用Mittag-Leffler展开定理,将“较大的”全纯函数分解为两个“较小的”全纯函数,此分解为我们更好地使用Levin-Lyubarski插值公式重构全纯函数
及
提供了环境。此外,该重构方法亦给出了该问题的解存在且唯一的充要条件。
本文将用
表示定义在
上的型为a的指数类全纯函数 [3] 。
2. 势函数的重构
设
为方程(1)满足初始条件
及
的解。由文 [4] 可得:
,(3)
其中
,
,
满足以下积分方程:
,
且对于两个变量分别存在一阶偏导数。此外,
,
.(4)
由(3)可得
(5)
其中
,且对于
,
。
定义
为方程(1)满足初始条件
,
的解。则
具有类似于(3)的表达式:
.(6)
故
,
有如下渐近式:
(7)
其中
,且对于
,
。
由于(1)~(2)的DD特征值
为特征值方程
(8)
的零点。由(3)可得,特征值函数的渐近式为:
,(9)
其中
。则当
时,DD特征值
的渐近式为:
(10)
其中
。
引理2.1 [5] [Theorem 3,6,2] 设
为亚纯函数,且当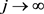 时,其单重极点
时,其单重极点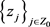 满足
满足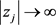 。记
。记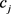 为
为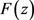 在
在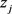 处的留数。若
处的留数。若
 ,(11)
,(11)
则存在全纯函数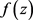 使得
使得
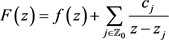 ,(12)
,(12)
其中,(12)式右侧的级数在 上任何不包含点
上任何不包含点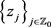 的有界子集上是一致收敛的。
的有界子集上是一致收敛的。
引理2.2 [6] [Theorem A]设f为sine类函数,其振幅宽度为2a,且其零点为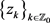 。则对于
。则对于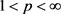 ,映射
,映射
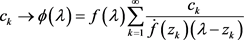 (13)
(13)
为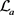 与
与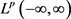 的同构映射,且在
的同构映射,且在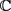 的任何子域上一致收敛。
的任何子域上一致收敛。
下面给出在 上重构q的方法及解存在的充要条件。定义
上重构q的方法及解存在的充要条件。定义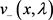 为方程(1)满足初始条件
为方程(1)满足初始条件 ,
,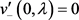 的解。类似可得
的解。类似可得
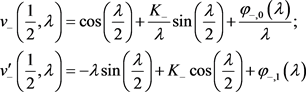 (14)
(14)
其中,对于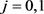 ,
,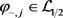 。记
。记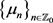 为
为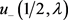 的零点,则
的零点,则
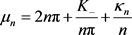 ,(15)
,(15)
其中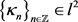 。显然
。显然 为亚纯函数且具有单重极点
为亚纯函数且具有单重极点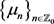 。设
。设 为函数
为函数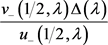 在
在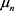 处的留数,则有
处的留数,则有
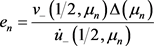 ,(16)
,(16)
其中 。由(5),(8)及(10)可得
。由(5),(8)及(10)可得
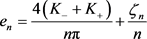 ,(17)
,(17)
其中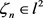 ,结合(15),可得
,结合(15),可得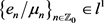 。由引理2.1,可知存在全纯函数
。由引理2.1,可知存在全纯函数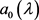 ,满足
,满足
 .(18)
.(18)
定义
 ,(19)
,(19)
则可得
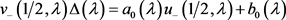 .(20)
.(20)
显然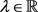 时,
时,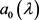 ,
,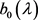 为全纯函数。
为全纯函数。
引理2.3 若记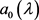 与
与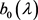 为
为
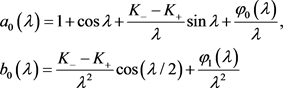 (21)
(21)
则 ,
,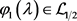 ,且
,且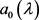 及
及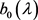 在展开式(20)中为唯一的。
在展开式(20)中为唯一的。
证明 注意到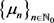 为
为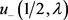 的零点,则由(20)可得
的零点,则由(20)可得
 (22)
(22)
将(15)带入计算,可得
 ,
,
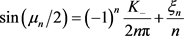 ,(23)
,(23)
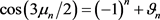 ,
,
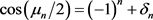 ,
,
其中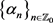 ,
,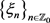 ,
, 均属于
均属于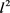 。进而将(23)带入(22)得到
。进而将(23)带入(22)得到
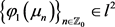 .(24)
.(24)
由于函数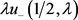 为sine类函数,且存在正整数
为sine类函数,且存在正整数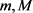 及p使得当
及p使得当 时,
时,
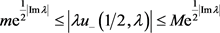
则结合(24),应用Levin-Lyubarski插值定理,即引理2.2,选取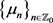 为重构函数
为重构函数 的插值节点,若记
的插值节点,若记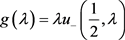 ,则有:
,则有:
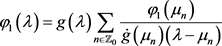 ,(25)
,(25)
其中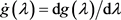 ,
,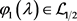 。
。
此外,Levin-Lyubarki插值定理保证了所重构函数的唯一性。故定理得证。
引理2.4 设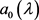 与
与 由(21)式定义。若
由(21)式定义。若
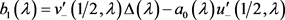 ,(26)
,(26)
则
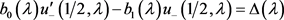 .(27)
.(27)
进而有
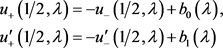 (28)
(28)
证明 由于
 ,(29)
,(29)
计算易得(27)成立。由于
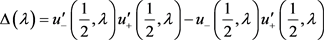 (30)
(30)
且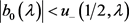 ,式(30)结合(27),可知存在
,式(30)结合(27),可知存在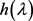 满足
满足
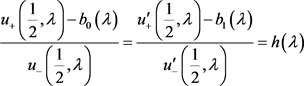 .(31)
.(31)
由(5)及(7)可知,当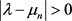 时,有
时,有
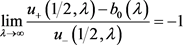 ,
,
故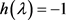 ,从而可得(28)。定理得证。
,从而可得(28)。定理得证。
注1 由引理2.3可知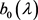 是唯一的. 由引理2.4可得
是唯一的. 由引理2.4可得 的表达式,进而可得
的表达式,进而可得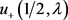 与
与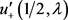 ,故有如下结论:
,故有如下结论:
定理2.5 设函数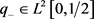 ,数列
,数列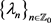 已知,且满足如下渐近式:
已知,且满足如下渐近式:
 (32)
(32)
其中A, ,
,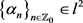 。若
。若
 (33)
(33)
其中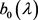 ,
,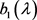 分别由(21)与(26)定义,且
分别由(21)与(26)定义,且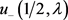 ,
,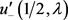 由(5)定义。
由(5)定义。
则存在唯一的实值函数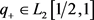 ,使得势函数q在
,使得势函数q在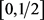 上满足
上满足 ,在
,在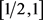 上,
上,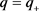 ,且其对应的算子以
,且其对应的算子以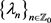 为特征值的充要条件是
为特征值的充要条件是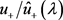 属于Nevanlinna类函数。
属于Nevanlinna类函数。
证明 必要性:假定存在实值函数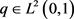 ,使得
,使得 为Sturm-Liouville算子的DD特征值。则由以上讨论可知,
为Sturm-Liouville算子的DD特征值。则由以上讨论可知,
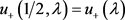 ,
, .
.
故由 [2] [7] 知,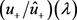 是Sturm-Liouville问题(1)~(2)的Weylm-函数 [7] ,故
是Sturm-Liouville问题(1)~(2)的Weylm-函数 [7] ,故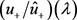 属于Nevanlinna类函数。
属于Nevanlinna类函数。
充分性:若实值函数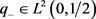 已知,则函数
已知,则函数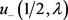 、
、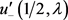 及
及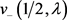 ,
,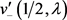 为已知函数。则由(5)、(14)及引理2.3得,
为已知函数。则由(5)、(14)及引理2.3得,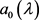 及
及 可知,又由于DD特征值已知,进而由(26)可得
可知,又由于DD特征值已知,进而由(26)可得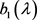 ,从而由(28)计算可得
,从而由(28)计算可得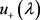 及
及 :
:
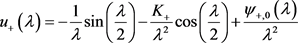 ,
,
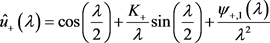 ,
,
其中 ,故
,故 可知。定理得证。
可知。定理得证。
基金项目
国家自然科学基金面上项目资助(11571212);陕西省大学生创新训练项目资助(1314)。
NOTES
*通讯作者。