1. 引言
在公元四、五世纪的《孙子算经》中的“物不知数”问题:“今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二,问物几何?”答案为:“23”。这个问题也就是求解同余式组
.
明朝程大位根据孙子算经里所用的方法用歌谣给出了该题的解法:“三人同行七十稀,五树梅花廿一枝,七子团圆月正半,除百零五便得知。”即解为
.
在西方,与《孙子算经》同类的算法,最早见于1202年意大利数学家斐波那契的《算经》。1801年,德国数学家高斯的《算术探究》中,才明确写出了这一问题的求法。
把孙子算经给出的结果加以推广,就得到了著名的孙子定理。孙子定理及其证明参阅 [1] [2] 。文 [3] 给出了一个求解孙子问题的简便方法。文 [4] 研究了一般的线性同余式组的有解判别条件及其求解方法。文 [5] 把线性同余式组、线性不定方程组、线性代数方程组、常系数线性微分方程组和常系数线性差分方程组统一成为了R-模上的方程组,并分别给出了各种方程组的解法。
2. 主要结果及应用
下面的定理1就是著名的孙子定理。
定理1 (孙子定理) 设
是k个两两互质的正整数,
,
则同余式组
.(1)
的解是
,(2)
其中
.(3)
文 [1] 给出了该定理的三种证明方法。下面我们再给出一种证法。
证 因
是k个两两互质的正整数,故
。于是,满足(3)式的整数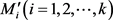 是存在的。
是存在的。
要证明同余式组(1)的解是(2),只需证明(1)式和(2)式等价即可。
设整数x满足(1)式,则
,从而
.
因为当
时,
,故
.
从而
.(4)
因
满足(3)式,故
.(5)
因
两两互质,故由(5)式得
(6)
由(4)和(6)两式即知,(2)式成立。
反之,设整数x满足(2)式,则由
和(3)式得
.
即整数x满足(1)式。
应用定理1求解孙子问题的例子参见文 [1] [2] 。下面给出一个更便于求解孙子问题的方法。
定理2 设
是k个两两互质的正整数,则同余式组(1)的解为
,(7)
其中,
,(8)
而
,
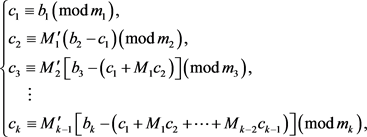 (9)
(9)
.(10)
证 因
两两互质,故满足(10)式的整数
是存在的。首先证明,
.(11)
显然,
.而当
时,由(8),(9)和(10)式得
.
要证明同余式组(1)的解是(7),只需证明(1)式和(7)式等价即可。设整数x满足(1)式,则
.(12)
由(11)和(12)式得
.
但
两两互质,故(7)式成立。
反之,设整数x 满足(7)式,则
.(13)
由(11)和(13)式得,(1)式成立。
推论 设
是k个两两互质的正整数,
,
,整数
满足
,
是
被
除所得的余数,
是
被
除所得的余数,
是
被
除所得的余数,
,
是
被
除所得的余数,则同余式组(1)的解为
,(14)
其中
。
证 根据定理2,(14)为同余式组(1)的解.下面证明
.
易知,
。故
,
,
.
例1 解同余式组
.
解 为了更便于应用定理2的推论求解,把这个同余式组改写为
.
这里,
。
.
取满足
即
的一个整数
。
取满足
即
的一个整数
。
取满足
即
的一个整数
。
,
,则
.
,
,则
.
,
,则
.
故由定理2的推论得,该同余式组的解为
.
例2 解同余式组
.
解 这里
,
.
由
取
。
由
取
。
由
取
。
由
取
。
由
取
,则
.
由
取
,则
.
由
,
取
,则
.
故由定理2得,同余式组的解为
,
即
.
参考文献