1. 前言
在国务院发布“关于进一步加强城市规划建设管理的意见”中,开放社区能否实现优化道路网络结构,提高道路交通能力,改善交通条件的目标以及改善效果如何成为了焦点问题,本文通过分析开放小区的影响指标,建立数学模型解决小区开放对道路通行的影响问题,并讨论其改善效果,对比不同类型小区开放后的交通情况,提出小区开放的合理化建议。
2. 问题假设
1) 小区居民不对开放小区进行道路封闭。2) 小区的位置对各个权重影响不大。3) 不同类型小区车辆覆盖率基本一致。4) 小区开放的成本相差无几。5) 小区开放期间不受其他自然灾害影响。
3. 问题分析 [1]
针对2016高教社杯全国大学生数学建模竞赛(CUMCM)题目B题中所涉及到的四个问题,展开以下分析:
针对问题一:考虑到影响开放小区交通情况的因素多种多样,每个因素对小区开放后的交通又有着不同程度影响,分析每个因素影响小区开放后交通情况程度的权重,建立相关的合理指标,运用多层次模糊综合分析评价法,对开放小区周围交通情况进行定性评价,总结小区开放对周边道路通行的影响。
针对问题二:通过问题一中分析的各个因素对小区交通影响的权重,考虑各个因素的不同影响,本文采取对每个因素进行逐个建立数学模型,得到各个因素的不同影响程度。
针对问题三:为探究小区开放的效果,它涉及到小区路网结构、通行能力、周边道路宽度密度。选取不同类型的小区进行开放,并与开放前的交通情况进行对比,应用问题二中建立的模型进行定量比较小区开放前后对道路通行的影响。
针对问题四:根据对问题三中不同类型小区开放的研究结果,从交通通行能力的角度出发,向城市规划和交通管理部门提出关于小区开放的合理化建议,注重关注适于开放的封闭型小区的类别和位置。
4. 小区开放对周边道路通行的影响的评价指标
通过查阅书籍和材料,总结了影响城市道路容量的主要因素,包括道路状况,交通状况和路网结构等等,社区开放后,原有小区的封闭道路系统将于城市主干道项链,将增加路网的密度,增加城市道路交叉口的数量。本文主要以路网结构、通行能力、道路宽度和密度、出行高峰时间及与市中心的距离为评价指标(见图1)。
Figure 1. Factors influencing traffic conditions in open residential areas
图1. 影响开放小区的交通情况的因素
4.1. 路网结构
1) 路网的供需能力比
如果路网的交通供应能力为
C 和需求量为
T ,则路网的饱和度(
LOS )可表示为:
LOS=TC (1)
a) 路网容量:
通常认为小区的路网容量与各种因素有关,比如城市的交通管理、路网拓扑结构、路上行人以及非机动车等多种因素有关。
b) 路网交通需求量:
一般来说,城市路网的交通需求量主要是由两个部分组成的,过境交通量和区内所有土地使用设施的生成量。如果这片区域的过境交通量为
T1 和使用设施的生成量为
T2 ,那么(1)中:
T=T1+T2 (2)
2) 利用路网时空饱和度指标
根据路网时空饱和度定义,路网LOS可表示为:
LOS=n⋅minPdvPs (3)
其中,机动车在有效营运时间
T 内的总车次为
n 。式中
n 是由两部分组成:
n=n1+n2 (4)
Ps 为道路网车道的时空资源:
Ps=Lv⋅t (5)
Pdv 为出行的时空资源消耗:
Pdv=hy⋅t (6)
4.2. 通行能力
根据以下公式计算机动车道的通行能力:
Np=3600ti (7)
当小区没有
ti 观测值时,可能通行能力可以如表1表示。
极速滚球-beplay滚球玩法刺激-beplay体育官网网页版等您来挑战!
| 计算行车速度 |
55~45 |
44~35 |
34~25 |
24~15 |
| 可能通行能力 |
1690 |
1640 |
1550 |
1360 |
Table 1. Vehicle speed and possible capacity
表1. 行车速度与可能通行能力
根据中华人民共和国道路交通安全法办法规定:机动车在道路上行驶不得超过限速标志、标线标明的速度。城市道路行车速度最高不得超过每小时50公里,通过小区的行车速度最高的速度不得超过每小时15公里。
计算没有受到平面交叉口影响的机动车道设计通行能力公式:
Nm=sc×Np (8)
其中,
sc 为机动车通行能力的分类系数如表2所示。
极速滚球-beplay滚球玩法刺激-beplay体育官网网页版等您来挑战!
| 道路分类 |
快速路 |
主干道 |
次干道 |
支路 |
|
|
0.70 |
0.75 |
0.80 |
0.85 |
Table 2. Classification coefficient of vehicle capacity
表2. 机动车通行能力分类系数
1) 根据交通流理论,反应 = 灵敏度 × 刺激。众所周知:
刺激=˙xi(t)−˙xi+1(t) ,
反应=¨xi+1(t+T) ,且灵敏度分析公式为:
灵敏度=a[xi(t)−xi+1(t)]m(a,m为待定参数)
因此:
¨xi+1(t+T)={a[xi(t)−xi+1(t)]m}(˙xi(t)−˙xi+1(t))
两边取积分
当
m=1 时,
˙xi(t+T)=aln[xi−1(t)−xi(t)]+c1 ;
当
m>1 时,
˙xi(t+T)=(1−m)−1aln[xi−1(t)−xi(t)] 。
考虑初始条件后,得到:
c2=−(1−m)−1alnL1−m0
综合起来:
当
m=1 时,
˙xi(t+T)=aln[xi−1(t)−xi(t)L0] ;
当
m>1 时,
˙xi(t+T)=(1−m)−1aln[xi−1(t)−xi(t)] 。
为方便起见,令车头间距
h0=xi−1(t)−xi(t),μ=xi(t+T).
车速(低车速)关系模型与小型车动态车头间距标准如下:
令
m=1 ,则
a=9 ,
μ=9⋅lnhs7 ,精度
θ=0.642 ;
令
m=2 ,则
a=84 ,
μ=98⋅(17−1hs) ,精度
θ=0.991 ;
令
m=3 ,则
a=730 ,
μ=360⋅(172−1hs2) ,精度
θ=0.859 ;
令
m=4 ,则
a=570 ,
μ=1920⋅(173−1hs3) ,精度
θ=0.727 。
因此,相应车距与作为小型车车头间距的关系模型为:
μ=98(17−1hs)(μ≤9 m/s) (9)
2) 道路通行能力
μ=98(17−1hs)(μ≤9 m/s) 。
通过调查小汽车通行能力,根据来进行计算。
因
hs=μht ,故
μ=14−98hsμ ,整理得
ht=98μ(14−μ) 。
于是小汽车在道路的理论通行能力为:
Cap=max1ht=maxμ(14−μ)98 (10)
根据上述公式,当
μ 变化的车头时距
ht 与每条车道的通行能力
Cap 见表3。
极速滚球-beplay滚球玩法刺激-beplay体育官网网页版等您来挑战!
|
|
|
|
| 8 |
2.04 |
1750 |
| 7 |
2 |
1800 |
| 6 |
2.04 |
1770 |
| 5 |
2.18 |
1640 |
Table 3. Headway time spacing and traffic capacity variable with vehicle speed
表3. 随车速而变化的车头时距与通行能力
4.3. 道路密度和间距
根据国际上使用的一些具有代表性的城市道路网络经验,在确定道路网密度时应注意要遵循以下几点原则:
1) 从交通的角度来看,道路网密度不能过稀和过密。
2) 道路网密度可以根据地区不同和交通管理控制方式而有所不同。
3) 但特殊地区可以另作考虑。
因此道路间距密度关系式为
1di−1di+1=fi2000 (11)
其中
di 是
i+1 等级道路围合区域内的
i 等级道路间距,
di+1 为高一等级道路间距,显然
di+1>di ,
fi 是
i+1 等级道路围合区域内的
i 等级道路密度。
5. 建立模型
5.1. 多层次模糊综合评价法
模糊综合分析评价 [2] 是一种基于模糊数学的综合评价的方法。综合评价法是根据模糊数学的隶属度理论将定性评价转化为定量评价的方法。当难以表达某种程度的定性指标时,这个时候就可以用模糊概念来表达,例如“很好”、“较好”、“较差”、“很差”等模糊概念来表示。
如果每个因素中还包括多个层次,且该因素又通常由若干因素决定,可以按以下做法:首先,根据最低层次的各个因素进行综合评价,然后根据前面一层次的各个因素进行综合评价,并且更上一层评价,直到评价到最高层次。从而能够得出总的综合评价结果,即所谓的多层次模糊综合评价法。
5.2. 模型建立步骤
第一步是要建立评价指标的体系 [3] ,评价指标体系指的是影响评价的因素。
首先,把这些因素先分为若干个子集,即第一层因素,并记为
U=(u1,u2,⋯,ui,⋯,un) ,
n∑i=1Ui=U,U∩Uj=ϕ(i≠j),(i,j=1,2,⋯,n) 。如果第
i 个因素有
s 个影响子因素,则为第二层因素,记为
Ui=(ui1,ui2,⋯,uis) ,依此类推。
第二步建立评价集;将评价集记为
v=(v1,v2,⋯,vm) 。并且将开放小区的交通情况的评价结果分成五个等级,记为
v=(v1,v2,v3,v4,v5)=(优,良,中,及格,不及格)
第三步是建立因素的权重集;在对开放小区的交通状况的评估中,采用模糊一致判断矩阵法来确定因素的权重,最大程度的消除主观因素的影响。
第四步利用0.1~0.9的比例来对因素集的因素进行分析,并且用表4的模糊度来对其进行描述并给出两两比较的模糊判断,从而得出模糊一致判断矩阵 [4] 。
极速滚球-beplay滚球玩法刺激-beplay体育官网网页版等您来挑战!
| 标度 |
定义 |
意义 |
| 0.5 |
同等重要 |
两元素相比较,同等重要 |
| 0.6 |
略微重要 |
两元素比较,一元素比另一元素稍微重要 |
| 0.7 |
明显重要 |
两元素比较,一元素比另一元素明显重要 |
| 0.8 |
重要得多 |
两元素比较,一元素比另一元素重要得多 |
| 0.9 |
极端重要 |
两元素相比较,一元素比另一元素极端重要 |
| 0.1,0.2, 0.3,0.4 |
反向比较 |
若元素
与元素
相比较得到判断
, 则元素
与元素
相比较得到的判断为
。 |
Table 4. Quantitative scale of 0.1 - 0.9
表4. 0.1~0.9的数量标度
A=(a11a12⋯a1na21a22⋯a2n⋮⋮⋮an1an2⋯ann) 。
其中
aij 表示“
ui 比
uj 重要”的隶属度。
根据以上因素权重,可以通过公式直接得出:
Ui 的权重
Wi=1n−12a+1nan∑i=1aij,i=1,2,⋯,n 。 (12)
a 的范围为
a≥n−12 ,表示
a 越大,权重之差越小;
a 越小,权重之差越大,当时权重差异达到最大值 [5] 。
第五步使用上述的方法获得第一层因子(指标)权重集:
W=(w1,w2,w3,w4,w5,w6) 。
利用相同的方法能够得到第二层因子(指标)权重集:
R=(wi1,wi2,⋯,wis),i=1,2,⋯,s
首先,建立模糊矩阵。
从而进行一级模糊综合评价,即先对每一个因素集
Ui 做出综合评判,即可构造出分别属于
n 个一级指标
ui 的模糊关系矩阵
Gi(1,2,⋯,n) 。
Gi=(gi11gi12⋯gi1mgi21gi22⋯gi2m⋮⋮⋮gis1gis2⋯gism)
其中矩阵
Gi 是假设
ui 有
s 个影响子因素,
m 为评价结果的等级数量,
gisf 表示第
i 个因素下第
s 个因素的第
s 种评判结果
1≤f≤m ,即
Uis 因素对第
f 个评语的隶属度。隶属度可以由公式
gish=dish2a 得出,其中 表示评价专家总人数,
表示评价专家总人数,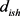 表示
表示 因素在第
因素在第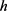 个评语获得专家认可人数。
个评语获得专家认可人数。 中各因素的权重为:
中各因素的权重为:
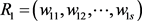
其中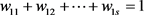 。
。
则一级综合评判为: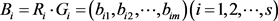 。然后,将
。然后,将 作为一个因素,用
作为一个因素,用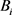 作它的评判矩阵。
作它的评判矩阵。
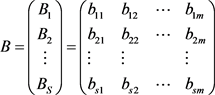
同样,把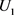 的指标因素权重集
的指标因素权重集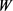 乘以
乘以 获得的综合评价结果为:
获得的综合评价结果为: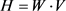 ,将分值赋予评价语
,将分值赋予评价语 中的每一个等级,最终可以得到目标层的综合得分
中的每一个等级,最终可以得到目标层的综合得分 ,即
,即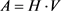 [6] 。
[6] 。
5.3. 模型求解
将开放小区的交通情况分为路网结构、通行能力、道路宽度和密度、出行高峰时间及与市中心的距离五个方面进行分析,即一级指标 有5个元素
有5个元素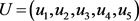 ,二级指标有:
,二级指标有: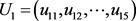 、
、 、
、 。各因素权重计算结果:给出成对比较的模糊判断,得到一级指标因素的模糊一致判断矩阵,并根据公式(1)计算各一级指标因素权重。由模糊一致判断矩阵方法确定的一级指标因素的权重集为:
。各因素权重计算结果:给出成对比较的模糊判断,得到一级指标因素的模糊一致判断矩阵,并根据公式(1)计算各一级指标因素权重。由模糊一致判断矩阵方法确定的一级指标因素的权重集为:
 ,
,
得到二级指标因素权重集:
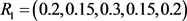 ;
;
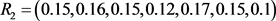 ;
;
 ;
;
接下来对开放小区的交通情况进行评价,评价结果统计如表5。
极速滚球-beplay滚球玩法刺激-beplay体育官网网页版等您来挑战!
| 一级指标 |
二级指标 |
优 |
良 |
中 |
及格 |
不及格 |
| 路网 结构 |
u11 |
7 |
3 |
0 |
0 |
0 |
| u12 |
7 |
2 |
1 |
0 |
0 |
| u13 |
8 |
2 |
0 |
0 |
0 |
| u14 |
6 |
4 |
0 |
0 |
0 |
| u15 |
7 |
3 |
0 |
0 |
0 |
| 通行 能力 |
u21 |
6 |
3 |
1 |
0 |
0 |
| u22 |
5 |
4 |
1 |
0 |
0 |
| u23 |
8 |
2 |
0 |
0 |
0 |
| u24 |
7 |
3 |
0 |
0 |
0 |
| u25 |
5 |
5 |
0 |
0 |
0 |
| u26 |
6 |
4 |
0 |
0 |
0 |
| u27 |
9 |
1 |
0 |
0 |
0 |
| 道路 密度和 间距 |
u31 |
7 |
2 |
1 |
0 |
0 |
| u32 |
5 |
4 |
1 |
0 |
0 |
| u33 |
8 |
2 |
0 |
0 |
0 |
| u34 |
1 |
4 |
3 |
1 |
1 |
| u35 |
4 |
3 |
1 |
1 |
1 |
| u36 |
7 |
1 |
1 |
1 |
0 |
| u37 |
6 |
3 |
1 |
0 |
0 |
Table 5. Scoring of traffic conditions affecting the opening of residential areas
表5. 影响小区开放的交通情况评分
根据表5,可以获得五个一级指标的模糊关系矩阵 ,其相应的模糊关系矩阵可表示为:
,其相应的模糊关系矩阵可表示为:
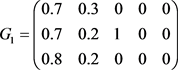
路网结构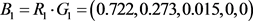 ;
;
通行能力: ;
;
道路宽度和密度: ;
;
出行高峰时间: ;
;
与中心的距离: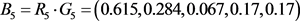 ;
;
于是,形成模糊评价矩阵
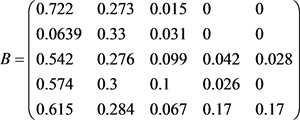
最后,通过用 的指标因素权重集
的指标因素权重集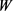 乘以
乘以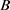 ,获得目标层的指标
,获得目标层的指标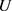 对评价语
对评价语 的隶属度。
的隶属度。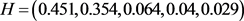 ,该隶属度可以表示有45.2%专家对该开放小区的交通状况评价为优、29.3%的专家评价认为该开放小区的交通状况质量为良、6.2%的专家评为为中等。假设对开放小区的交通状况的评价结果做相应的百分制对应,设(优,良,中,及格,不及格) = (100~91,90~81,80~71,70~61,60及60以下)。并且取每一级分数本级的中位数的近似数,即(优,良,中,及格,不及格) = (95, 85, 75, 65, 55),最终获得目标层的总分,分数为
,该隶属度可以表示有45.2%专家对该开放小区的交通状况评价为优、29.3%的专家评价认为该开放小区的交通状况质量为良、6.2%的专家评为为中等。假设对开放小区的交通状况的评价结果做相应的百分制对应,设(优,良,中,及格,不及格) = (100~91,90~81,80~71,70~61,60及60以下)。并且取每一级分数本级的中位数的近似数,即(优,良,中,及格,不及格) = (95, 85, 75, 65, 55),最终获得目标层的总分,分数为 分,即该开放小区的交通情况模糊综合评价得分为82分。
分,即该开放小区的交通情况模糊综合评价得分为82分。
6. 各类型小区开放前后对道路通行的影响
6.1. 道路结构划分
中国现有的住宅区基本上是分为三种基本的道路模式:格网模式、内环模式和外环模式这三种基本的道路模式。为了结合问题二的数学模型,这里引进交通可达性、效率性、安全性三个评价指标:
由以上描述,根据表6并结合数学模型可以对道路结构计算得分,分别取高:0.1,中:0.2,低:0.3为标准,得到每个评价指标下的得分(见表7)。
极速滚球-beplay滚球玩法刺激-beplay体育官网网页版等您来挑战!
| |
格网模式 |
内环模式 |
外环模式 |
| 交通可达性 |
高 |
中 |
低 |
| 交通效率性 |
高 |
中 |
低 |
| 交通安全性 |
低 |
中 |
高 |
Table 6. Traffic conditions of various types of road structures (grades)
表6. 各类型道路结构交通情况(等级)
极速滚球-beplay滚球玩法刺激-beplay体育官网网页版等您来挑战!
| |
格网模式 |
内环模式 |
外环模式 |
| 交通可达性 |
0.3 |
0.2 |
0.1 |
| 交通效率性 |
0.3 |
0.2 |
0.1 |
| 交通安全性 |
0.1 |
0.2 |
0.3 |
Table 7. Traffic conditions of various types of road structures (scoring)
表7. 各类型道路结构交通情况(评分)
6.2. 通行能力
对于住在区内的道路,基本上可以呈现以下三种形式:有贯通式(曲线式、直线式)、环通式、尽端式,如图2~图4所示(表8)。
极速滚球-beplay滚球玩法刺激-beplay体育官网网页版等您来挑战!
| |
贯通式道路 |
环通式道路 |
尽端式道路 |
| 交通通行能力 |
0.6 |
0.8 |
0.3 |
Table 8. Traffic conditions on various roads
表8. 各式道路的交通情况
6.3. 道路密度和间距
道路密度考虑到小区内部道路覆盖率有明显差别,也是重要的指标。这里给出这一指标的模糊综合评价法的得分见表9。
极速滚球-beplay滚球玩法刺激-beplay体育官网网页版等您来挑战!
| |
道路密度高 |
道路密度中 |
道路密度低 |
| 道路间距大 |
0.9 |
0.6 |
0.4 |
| 道路间距中 |
0.6 |
0.4 |
0.2 |
| 道路间距小 |
0.4 |
0.2 |
0.1 |
Table 9. Effects of road density and spacing on traffic in residential areas
表9. 道路密度和间距对小区交通的影响
6.4. 结合福州市某小区分析小区开放的结果
综合以上三个指标的得分,取平均数后参照模糊综合评价法的五个等级得到小区的综合得分,根据小区的得分判断是否进行开放,现在为探究小区开放的结果,选取了福州市某一个小区为案例进行分析见图5。

Figure 5. Road layout before community opening
图5. 小区开放前道路布局
通常小区路网结构分为外环式、环通式和道路密度低间距中,对照表9道路密度和间距对小区交通的影响,可以分析得出该小区的得分并取平均值为0.5,现在假设对小区开放,这里通过道路仿真模拟拟合得出开放效果如图6。
根据图6中小区开放后道路布局情况得出表10路段可靠度的分析结果。
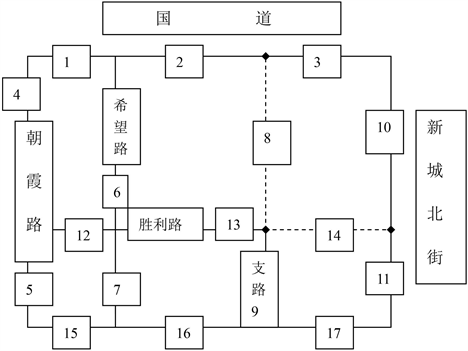
Figure 6. Road layout after community opening
图6. 小区开放后道路布局
极速滚球-beplay滚球玩法刺激-beplay体育官网网页版等您来挑战!
| 路段编号 |
可靠度 |
路段编号 |
可靠度 |
路段编号 |
可靠度 |
| 1 |
0.67 |
7 |
0.67 |
13 |
0.50 |
| 2 |
0.58 |
8 |
0.75 |
14 |
0.50 |
| 3 |
0.58 |
9 |
0.75 |
15 |
0.58 |
| 4 |
0.67 |
10 |
0.67 |
16 |
0.58 |
| 5 |
0.67 |
11 |
0.67 |
17 |
0.50 |
| 6 |
0.58 |
12 |
0.58 |
|
|
Table 10. Analysis results of section reliability
表10. 路段可靠度的分析结果
根据路段可靠性的分析结果,从表10得到的局部道路网的可靠性从小区内部道路使用前0.3707增加到小区道路使用后的0.4371,因此,它可改善局部路网交通状况。因而,在道路资源紧张的情况下,在小区内部对道路进行开放使用具有重要的作用。
7. 关于小区开放的合理化建议
7.1. 小区开放原则
为了提高城市道路密度和以下等级的道路网络,将建立城市微循环交通系统,进一步缓解城市交通压力。为了增加道路支路密度和建立微循环,可以通过连接封闭型城市的小区端头路以此来增加道路支路,并且可以使用交通管理使交通有序运行。
根据我国目前城市交通现状和上述封闭型小区问题,为使封闭型小区交通开放带来更多社会效益,提出以下几点建议:
1) 将开放社区纳入执法机构的执法范围,依法收费,规范开放式小区道路交通秩序。
2) 小区开放时,将会有大量车辆进入小区,因此交通管理部门应将开放小区划入管理范围内。
3) 通过上述建立层次模糊分析法模型并对其结果分析得出,在影响小区道路通行的因素中也会产生相互影响。例如:小区路网结构与道路密度和间距之间相互制约的关系。因此,在小区道路的规划中,应根据小区的类型和小区的地理位置采取相应的措施,从而实现小区开放。
小区类型按功能可以分为:住宅、办公、教育、医疗等其它功能性的小区;根据定义将适用于道路开放的封闭型小区可以从以下几个方面分类,例如几何形状、功能、完整性等;从几何形状,它可以分成面积大于120,000 m2和单边长大于为150 m两种类型的小区;此外,从地区的完整性可分为两种类型的单元:整体型和组合型类型(见表11)。
极速滚球-beplay滚球玩法刺激-beplay体育官网网页版等您来挑战!
| 种类 |
类别 |
条件 |
| 功 能 |
居住 |
主要以居住为主,对小区其它方面以及与外界道路连接造成影响小 |
| 办公 |
文中办公指事业单位、行政单位、大型公司等,满足几何要求前提下, 必须进行交通开放时,小区及外围需做交通评价,根据结果判断 |
| 教育 |
只针对职业性学校、大学等单位,对于小学、初中、高中不作考虑 |
| 医疗 |
医疗用地对该区域交通影响较大。采取其他措施效果不佳,迫不得已时进行交通开放 |
| 商业 |
规模较大的商业区。内部交通对外封闭,且对其沿主要道路造成影响 |
| 混合 |
多种用地性质的组合,该区域的交通开放可沿边界进行交通开放 |
| 几 何 |
面积 |
小区交通开放面积应120,000 m2 |
| 边长 |
单向边长 ≥ 150 m |
| 完 整 性 |
组合式 |
由城市道路围合的区域内为封闭型,该区域内有多种功能用地, 依据周围路网及小单位产生交通量考虑交通开放 |
| 整体性 |
一个小区外围由城市主要道路围合而成, 用地性质、功能单一,且无小区之间交界的存在 |
Table 11. Closed residential quarters suitable for open road
表11. 适用于开放道路的封闭型小区
7.2. 改善内容及依据
7.2.1. 改善内容
从封闭型到交通开放型小区,打破人们日常交通、出行、居住、教育、办公等习惯的过程。小区开放是为居民提供一个良好的交通环境,但小区交通安全不可忽略,因此缓解城市交通拥堵是本文的最终目的,需要进行改善的项目有:
新通小区间道路线形及宽度设计;
涉及的小区出入口及小区道路出入设计;
小区交通组织及设施改善;
小区道路绿化设计,噪声防治措施;
7.2.2. 改善措施依据
交通开放小区相关设施的改善,是为了在小区交通开放后,既适于居住又创造一个良好的交通环境。本文进行相关设施改善的依据主要有:参考国外一些相关规划设计理念;同时为了与城市大交通环境的融合,还要根据城市的总体规划开展工作。

