, 其中φ是欧拉φ函数， ，且χ是一个模n的导子为d的狄利克雷特征。在本文中，我们运用狄利克雷特征的正交性和初等计算去重新证明上述等式[2]。

Abstract: Li, Hu and Kim [1] proved the following generalization of the Menon-Sury identity by using the filtrations of the ring   Z _nand its unit group Z ^* _n:

文章引用：陈曼. 带有一个狄利克雷特征的Menon-Sury恒等式[J]. 理论数学, 2019, 9(2): 188-194. https://doi.org/10.12677/PM.2019.92024

1. 引言

1965年，P.K. Menon [3] 发现了下面这个漂亮的恒等式

${\displaystyle \underset{\begin{array}{c}1\le k\le n\\ \gcd \left(k,n\right)=1\end{array}}{\sum }\gcd \left(k-1,n\right)}=\phi \left(n\right)\tau \left(n\right)$ (1)

其中 $n\in N=\{1,2,\cdots \}$ ， $\phi$ 是欧拉 $\phi$ 函数，且 $\tau \left(n\right)$ 是n的因子个数。2009年，Sury [4] 把这个恒等式推广成下面的形式：

${\displaystyle \underset{\begin{array}{c}1\le k,b_1,b_2,\cdots ,b_r\le n\\ \gcd \left(k,n\right)=1\end{array}}{\sum }\gcd \left(k-1,b_1,b_2,\cdots ,b_r,n\right)}=\phi \left(n\right){\sigma }_r\left(n\right)$ (2)

其中 ${\sigma }_r\left(n\right)={\displaystyle \underset{d|n}{\sum }{d}^r}$ 。Menon-Sury恒等式也可以被推广到模为有限剩余的Dedekind整环。这个方向在2014

年第一次被Miguel用Burnside引理和交换环理论完成 [5] [6] 。2017年，Zhao和Cao [7] 得到了带有一个狄利克雷特征形式的Menon恒等式：

${\displaystyle \underset{\begin{array}{c}1\le k\le n\\ \gcd \left(k,n\right)=1\end{array}}{\sum }\gcd \left(k-1,n\right)\chi \left(k\right)}=\phi \left(n\right)\tau \left(\frac{n}{d}\right)$ (3)

然后Toth通过考虑偶算术函数(模n)用另一种方法将上述等式加以进一步推广，作为应用，他也得到了有关Ramanujan和的相关公式。最近，Li，Hu和Kim [1] 对(2)，(3)作进一步推广，并且证明了下面两个定理。

定理1.1 ( [1] Li，Hu和Kim)：如果 $\chi$ 是一个模n的本原的狄利克雷特征，则我们有下面的恒等式：

${\displaystyle \underset{\begin{array}{c}1\le k,b_1,b_2,\cdots ,b_r\le n\\ \gcd \left(k,n\right)=1\end{array}}{\sum }\gcd \left(k-1,b_1,b_2,\cdots ,b_r,n\right)\chi \left(k\right)}=\phi \left(n\right)$ 。

定理1.2 ( [1] Li，Hu和Kim)：如果 $n,b_1,b_2,\cdots ,b_r\in N$ ，是一个模n的导子为d的狄利克雷特征，则我们有下面的恒等式：

${\displaystyle \underset{\begin{array}{c}1\le k,b_1,b_2,\cdots ,b_r\le n\\ \gcd \left(k,n\right)=1\end{array}}{\sum }\gcd \left(k-1,b_1,b_2,\cdots ,b_r,n\right)\chi \left(k\right)}=\phi \left(n\right){\sigma }_r\left(\frac{n}{d}\right)$ 。

注记：在定理1.2中令 $\chi ={\chi }_0$ ，即平凡特征，我们得到Menon-Sury恒等式(2)。令 $$ ，我们得到Zhao和Cao的恒等式(3)。

本文的主要任务是运用狄利克雷特征的正交性和初等计算重新证明上面两个结果。

2. 定理1.1的证明

为了证明我们的结论，需要下面四个引理。

引理2.1：如果p是一个素数，满足 $m<a$ 且 $\chi$ 是一个模 $p^a$ 的本原特征，则我们有

${\displaystyle \underset{u=1}{\overset{p^{a-m}}{\sum }}\chi \left(1+u{p}^m\right)}=0$ 。

证明：设 $U=\{\overline{1+u{p}^m}|1\le u\le p^{a-m}\}$ 是 ${\left(Z/p^{a}Z\right)}^{*}$ 的一个子群。定义一个同态

$\begin{array}{l}f:{\left(Z/p^{a}Z\right)}^{*}\to {\left(Z/p^{m}Z\right)}^{*}\\ \bar{a}\mapsto \bar{a}\end{array}$ ，

我们得到 $\ker f=U$ 。事实上，设 $\bar{b}=\overline{1+u{p}^m}\in U$ ，我们有 $f\left(\bar{b}\right)=\bar{b}=\bar{1}\left(\mathrm{mod}{p}^m\right)$ 和 $U\subset \ker f$ 。因为

$\text{\#}\ker f=\frac{\phi \left(p^a\right)}{\phi \left(p^m\right)}=\frac{p^{a-1}\left(p-1\right)}{p^{m-1}\left(p-1\right)}=p^{a-m}=\#U$ ，

又由第一同构定理，我们有

${\left(Z/p^{a}Z\right)}^{*}/\ker f\cong {\left(Z/p^{m}Z\right)}^{*}$ ，

所以 $\ker f=U$ 。而且，因为 $\chi$ 是一个模 $p^a\left(a>m\right)$ 的本原特征， $\chi |{}_U$ 在U上是一个非平凡特征。由狄利克雷特征的正交性，我们得到

${\displaystyle \underset{s\in U}{\sum }\chi \left(s\right)}=0={\displaystyle \underset{u=1}{\overset{p^{a-m}}{\sum }}\chi \left(1+u{p}^m\right)}$ 。

引理2.2 ( [1] ，引理2.4)：如果p是一个素数，自然数 $a,m,r,b_1,b_2,\cdots ,b_r$ 满足 $a-m-1\ge 0$ ，则我们有

${\displaystyle \underset{\begin{array}{c}1\le k,b_1,b_2,\cdots ,b_r\le p^a\\ \gcd \left(b_1,b_2,\cdots ,b_r,p^a\right)=p^m\end{array}}{\sum }1}={\left(p^{a-m}\right)}^r-{\left(p^{a-m-1}\right)}^r$ 。

引理2.3 ( [7] ，引理2.1])：设p是一个素数，n是一个正整数，且 $\chi$ 是一个模 $p^n$ 的本原的狄利克雷特征，如果m是一个正整数且 $1\le m<n$ ，则我们有

${\displaystyle \underset{\begin{array}{c}1\le k\le p^{n-m}\\ \gcd \left(k,p\right)=1\end{array}}{\sum }\chi \left(k{p}^m+1\right)}=\{\begin{array}{l}0,1\le m<n-1;\\ -1,m=n-1.\end{array}$

引理2.4 ( [7] ，引理2.4])：设p是一个素数，n是一个正整数，且 $\chi$ 是一个模 $p^n$ 的非平凡的狄利克雷特征，再设 $p^l\left(1\le l\le n\right)$ 是 $\chi$ 的导子，如果m是一个正整数且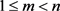，则我们有

${\displaystyle \underset{\begin{array}{c}1\le k\le p^{n-m}\\ \gcd \left(k,p\right)=1\end{array}}{\sum }\chi \left(k{p}^m+1\right)}=\{\begin{array}{l}\phi \left(p^{n-m}\right),l\le m<n;\\ -p^{n-l},m=l-1;\\ 0,1\le m<l-1.\end{array}$

定理1.1的证明：

记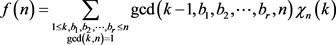。其中 ${\chi }_n$ 为一个模n的狄利克雷特征，存在使得 $\gcd \left(s,t\right)=1$ ，且成立下面等式：

$\begin{array}{l}f\left(st\right)={\displaystyle \underset{\begin{array}{c}1\le k,b_1,b_2,\cdots ,b_r\le st\\ \gcd \left(k,st\right)=1\end{array}}{\sum }\gcd \left(k-1,b_1,b_2,\cdots ,b_r,st\right){\chi }_{st}\left(k\right)}\\ ={\displaystyle \underset{\begin{array}{c}1\le k_1,b_1,b_2,\cdots ,b_r\le s\\ \gcd \left(k_1,s\right)=1\end{array}}{\sum }{\displaystyle \underset{\begin{array}{c}1\le k_2,b_1,b_2,\cdots ,b_r\le t\\ \gcd \left(k_2,t\right)=1\end{array}}{\sum }\gcd \left(k_{1}t+k_{2}s-1,b_1,b_2,\cdots ,b_r,st\right){\chi }_s\left(k_{1}t+k_{2}s\right){\chi }_t\left(k_{1}t+k_{2}s\right)}}\\ ={\displaystyle \underset{\begin{array}{c}1\le k_1,b_1,b_2,\cdots ,b_r\le s\\ \gcd \left(k_1,s\right)=1\end{array}}{\sum }{\displaystyle \underset{\begin{array}{c}1\le k_2,b_1,b_2,\cdots ,b_r\le t\\ \gcd \left(k_2,t\right)=1\end{array}}{\sum }\gcd \left(k_{1}t-1,b_1,b_2,\cdots ,b_r,s\right)\gcd \left(k_{2}s-1,b_1,b_2,\cdots ,b_r,t\right){\chi }_s\left(k_{1}t\right){\chi }_t\left(k_{2}s\right)}}\\ =f\left(s\right)f\left(t\right)\end{array}$ (4)

从(4)式我们可以看出f是积性函数，而且每一个模k的狄利克雷特征 $\chi$ 都能够被唯一的写成这种形式的乘积 $\chi ={\chi }_{k_1}{\chi }_{k_2}\cdots {\chi }_{k_r}$ ，其中 $k=k_1{k}_2\cdots k_r$ ， $\gcd \left(k_i,k_j\right)=1$ ， $i\ne j$ ，且 ${\chi }_{k_i}$ 是模 $k_i$ 的特征。再者，如果 $\chi$ 是本原的，则每一个 ${\chi }_{k_i}$ 模 $k_i$ 也是本原的。因此如果我们能证明对每一个 $p^a$ ，有 $f\left(p^a\right)=\phi \left(p^a\right)$ 成立，那么定理1的证明就完成了。为此，我们现在来计算 $f\left(p^a\right)$ ：

$\begin{array}{l}f\left(p^a\right)={\displaystyle \underset{\begin{array}{c}1\le k,b_1,b_2,\cdots ,b_r\le p^a\\ \gcd \left(k,p^a\right)=1\end{array}}{\sum }\gcd \left(k-1,b_1,b_2,\cdots ,b_r,p^a\right){\chi }_{p^a}\left(k\right)}\\ ={\displaystyle \underset{1\le k,b_1,b_2,\cdots ,b_r\le p^a}{\sum }\gcd \left(k-1,b_1,b_2,\cdots ,b_r,p^a\right){\chi }_{p^a}\left(k\right)}\\ ={\displaystyle \underset{\begin{array}{c}1\le k,b_1,b_2,\cdots ,b_r\le p^a\\ \gcd \left(k-1,b_1,b_2,\cdots ,b_r,p^a\right)\ne 1\end{array}}{\sum }\gcd \left(k-1,b_1,b_2,\cdots ,b_r,p^a\right){\chi }_{p^a}\left(k\right)}+{\displaystyle \underset{\begin{array}{c}1\le k,b_1,b_2,\cdots ,b_r\le p^a\\ \gcd \left(k-1,b_1,b_2,\cdots ,b_r,p^a\right)=1\end{array}}{\sum }{\chi }_{p^a}\left(k\right)}\\ ={\displaystyle \underset{m=1}{\overset{a}{\sum }}{\displaystyle \underset{\begin{array}{c}1\le k,b_1,b_2,\cdots ,b_r\le p^a\\ \gcd \left(k-1,b_1,b_2,\cdots ,b_r,p^a\right)=p^m\end{array}}{\sum }{p}^m{\chi }_{p^a}\left(k\right)}}-{\displaystyle \underset{m=1}{\overset{a}{\sum }}{\displaystyle \underset{\begin{array}{c}1\le k,b_1,b_2,\cdots ,b_r\le p^a\\ \gcd \left(k-1,b_1,b_2,\cdots ,b_r,p^a\right)=p^m\end{array}}{\sum }{\chi }_{p^a}\left(k\right)}+}{\displaystyle \underset{1\le b_1,b_2,\cdots ,b_r\le p^a}{\sum }{\displaystyle \underset{1\le k\le p^a}{\sum }{\chi }_{p^a}\left(k\right)}}\\ ={\displaystyle \underset{m=1}{\overset{a}{\sum }}{\displaystyle \underset{\begin{array}{c}1\le k,b_1,b_2,\cdots ,b_r\le p^a\\ \gcd \left(k-1,b_1,b_2,\cdots ,b_r,p^a\right)=p^m\end{array}}{\sum }\left(p^m-1\right){\chi }_{p^a}\left(k\right)}}+{\displaystyle \underset{1\le b_1,b_2,\cdots ,b_r\le p^a}{\sum }0}\end{array}$

上面最后一个等式是由引理2.3得到，最后由引理2.1，我们有：

$f\left(p^a\right)=\phi \left(p^a\right)+{\displaystyle \underset{m=1}{\overset{a-1}{\sum }}\left(p^m-1\right)}{\displaystyle \underset{\begin{array}{c}1\le b_1,b_2,\cdots ,b_r\le p^a\\ \gcd \left(b_1,b_2,\cdots ,b_r,p^a\right)=p^m\end{array}}{\sum }0}=\phi \left(p^a\right)$ 。

所以我们完成了定理1.1的证明。

3. 定理1.2的证明

首先，我们需要证明下面的命题。

命题3.1：如果 $\chi$ 是一个模 $p^a$ 的一个狄利克雷特征，且 $p^l\left(0\le l\le a\right)$ 是 $\chi$ 的导子，则我们有下列恒等式：

${\displaystyle \underset{\begin{array}{c}1\le k,b_1,b_2,\cdots ,b_r\le p^a\\ \gcd \left(k,p^a\right)=1\end{array}}{\sum }\gcd \left(k-1,b_1,b_2,\cdots ,b_r,p^a\right)\chi \left(k\right)}=\phi \left(p^a\right){\sigma }_r\left(\frac{p^a}{p^l}\right)$ 。

证明：如果 $l=0$ ，则 $\chi$ 是一个平凡特征，上式退化为Sury的恒等式(2)。如果 $l=a$ ，则 $\chi$ 是一个模 $p^a$ 的本原特征，这时候上式就是定理1.1。对于剩下的情形，根据定理1.1的证明，我们有

$\begin{array}{l}{\displaystyle \underset{\begin{array}{c}1\le k,b_1,b_2,\cdots ,b_r\le p^a\\ \gcd \left(k,p^a\right)=1\end{array}}{\sum }\gcd \left(k-1,b_1,b_2,\cdots ,b_r,p^a\right){\chi }_{p^a}\left(k\right)}\\ =p^a-1+{\displaystyle \underset{m=1}{\overset{a-1}{\sum }}\left(p^m-1\right)}{\displaystyle \underset{\begin{array}{c}1\le k\le p^a\\ \gcd \left(k-1,p^a\right)=p^m\\ m\ne a\end{array}}{\sum }{\chi }_{p^a}\left(k\right)}+{\displaystyle \underset{m=1}{\overset{a-1}{\sum }}\left(p^m-1\right)}{\displaystyle \underset{\begin{array}{c}1\le b_1,b_2,\cdots ,b_r\le p^a\\ \gcd \left(b_1,b_2,\cdots ,b_r,p^a\right)=p^m\\ m<a\end{array}}{\sum }{\displaystyle \underset{\begin{array}{c}1\le k\le p^a\\ \gcd \left(k-1,p^m\right)=p^m\end{array}}{\sum }{\chi }_{p^a}\left(k\right)}}\\ +{\displaystyle \underset{m=1}{\overset{a-2}{\sum }}\left(p^m-1\right)}{\displaystyle \underset{\begin{array}{c}1\le b_1,b_2,\cdots ,b_r\le p^a\\ \gcd \left(b_1,b_2,\cdots ,b_r,p^a\right)=p^s\\ m<s<a\end{array}}{\sum }{\displaystyle \underset{\begin{array}{c}1\le k\le p^a\\ \gcd \left(k-1,p^s\right)=p^m\end{array}}{\sum }{\chi }_{p^a}(k)}}\end{array}$

为了方便记号，将上面各项简记为：

$\begin{array}{l}A=p^a-1,\\ B={\displaystyle \underset{m=1}{\overset{a-1}{\sum }}\left(p^m-1\right)}{\displaystyle \underset{\begin{array}{c}1\le k\le p^a\\ \gcd \left(k-1,p^a\right)=p^m\\ m\ne a\end{array}}{\sum }{\chi }_{p^a}\left(k\right)},\\ C={\displaystyle \underset{m=1}{\overset{a-1}{\sum }}\left(p^m-1\right)}{\displaystyle \underset{\begin{array}{c}1\le b_1,b_2,\cdots ,b_r\le p^a\\ \gcd \left(b_1,b_2,\cdots ,b_r,p^a\right)=p^m\\ m<a\end{array}}{\sum }{\displaystyle \underset{\begin{array}{c}1\le k\le p^a\\ \gcd \left(k-1,p^m\right)=p^m\end{array}}{\sum }{\chi }_{p^a}\left(k\right)}},\\ D={\displaystyle \underset{m=1}{\overset{a-2}{\sum }}\left(p^m-1\right)}{\displaystyle \underset{\begin{array}{c}1\le b_1,b_2,\cdots ,b_r\le p^a\\ \gcd \left(b_1,b_2,\cdots ,b_r,p^a\right)=p^s\\ m<s<a\end{array}}{\sum }{\displaystyle \underset{\begin{array}{c}1\le k\le p^a\\ \gcd \left(k-1,p^s\right)=p^m\end{array}}{\sum }{\chi }_{p^a}(k)}}\end{array}$

现在分别计算B, C, D各项。由引理2.4，我们有

$\begin{array}{c}B={\displaystyle \underset{m=1}{\overset{a-1}{\sum }}\left(p^m-1\right)}{\displaystyle \underset{\begin{array}{c}1\le j\le p^{a-m}\\ \gcd \left(j,p\right)=1\end{array}}{\sum }{\chi }_{p^a}\left(1+j{p}^m\right)}\\ ={\displaystyle \underset{m=1}{\overset{l-1}{\sum }}\left(p^m-1\right)}{\displaystyle \underset{\begin{array}{c}1\le j\le p^{a-m}\\ \gcd \left(j,p\right)=1\end{array}}{\sum }{\chi }_{p^a}\left(1+j{p}^m\right)}+{\displaystyle \underset{m=l}{\overset{a-1}{\sum }}\left(p^m-1\right)}{\displaystyle \underset{\begin{array}{c}1\le j\le p^{a-m}\\ \gcd \left(j,p\right)=1\end{array}}{\sum }{\chi }_{p^a}\left(1+j{p}^m\right)}\end{array}$

$=1-p^{a-1}+\left(a-l\right)\phi (pa)$

再由引理2.2，我们得到：

$\begin{array}{c}C={\displaystyle \underset{m=1}{\overset{a-1}{\sum }}\left(p^m-1\right)}\left({\left(p^{a-m}\right)}^r-{\left(p^{a-m-1}\right)}^r\right){\displaystyle \underset{1\le u\le p^{a-m}}{\sum }{\chi }_{p^a}\left(1+u{p}^m\right)}\\ ={\displaystyle \underset{m=1}{\overset{a-1}{\sum }}\left(p^m-1\right)}\left({\left(p^{a-m}\right)}^r-{\left(p^{a-m-1}\right)}^r\right){\displaystyle \underset{i=0}{\overset{a-m}{\sum }}{\displaystyle \underset{\begin{array}{c}1\le v\le p^{a-m-i}\\ \text{gcd}\left(v,p\right)=1\end{array}}{\sum }{\chi }_{p^a}\left(1+v{p}^{m+i}\right)}}\\ ={\displaystyle \underset{m=1}{\overset{a-1}{\sum }}\left(p^m-1\right)}\left({\left(p^{a-m}\right)}^r-{\left(p^{a-m-1}\right)}^r\right){\displaystyle \underset{i=0}{\overset{a-m}{\sum }}{\displaystyle \underset{\begin{array}{c}1\le v\le p^{a-w}\\ \text{gcd}\left(v,p\right)=1\end{array}}{\sum }{\chi }_{p^a}\left(1+v{p}^w\right)}}\end{array}$

接着再由引理2.4，得到

$\begin{array}{c}C={\displaystyle \underset{m=1}{\overset{l-2}{\sum }}\left(p^m-1\right)}\left({\left(p^{a-m}\right)}^r-{\left(p^{a-m-1}\right)}^r\right)\left(-p^{a-l}+{\displaystyle \underset{i=l-m}{\overset{a-m-1}{\sum }}\phi \left(p^{a-m-i}\right)+1}\right)\\ +\left(p^{l-1}-1\right)\left({\left(p^{a-\left(l-1\right)}\right)}^r-{\left(p^{a-\left(l-1\right)-1}\right)}^r\right)\left(-p^{a-l}+{\displaystyle \underset{i=1}{\overset{a-l}{\sum }}\phi \left(p^{a-\left(l-1\right)-i}\right)+1}\right)\\ +{\displaystyle \underset{m=l}{\overset{a-1}{\sum }}\left(p^m-1\right)}\left({\left(p^{a-m}\right)}^r-{\left(p^{a-m-1}\right)}^r\right)\left({\displaystyle \underset{i=0}{\overset{a-m-1}{\sum }}\phi \left(p^{a-m-i}\right)+1}\right)\\ =0+0+p^a\left(p^{ar}-p^{ar-r}\right){\displaystyle \underset{m=l}{\overset{a-1}{\sum }}\left(1-p^{-m}\right)p^{-mr}}\\ =p^{ar+a-rl}-p^a-\frac{\left(p^{1+r}-p\right)\left(p^{ar+a-l-rl}-1\right)}{p^{1+r}-1}\end{array}$

最后，由引理2.2和引理2.4计算D，得到

$\begin{array}{c}D={\displaystyle \underset{m=1}{\overset{a-2}{\sum }}\left(p^m-1\right)}{\displaystyle \underset{s=m+1}{\overset{a-1}{\sum }}{\displaystyle \underset{\begin{array}{c}1\le b_1,b_2,\cdots ,b_r\le p^a\\ \gcd \left(b_1,b_2,\cdots ,b_r,p^a\right)=p^s\end{array}}{\sum }{\displaystyle \underset{\begin{array}{c}1\le j\le p^{a-m}\\ \gcd \left(j,p\right)=1\end{array}}{\sum }{\chi }_{p^a}\left(1+j{p}^m\right)}}}\\ =p^{ar-r}{\displaystyle \underset{m=1}{\overset{a-2}{\sum }}\left(p^m-1\right)p^{-mr}}\left(1-{\left(p^{-r}\right)}^{a-m-1}\right){\displaystyle \underset{\begin{array}{c}1\le j\le p^{a-m}\\ \gcd \left(j,p\right)=1\end{array}}{\sum }{\chi }_{p^a}\left(1+j{p}^m\right)}\\ =p^{ar-r}{\displaystyle \underset{m=1}{\overset{l-1}{\sum }}\left(p^m-1\right)p^{-mr}}\left(1-{\left(p^{-r}\right)}^{a-m-1}\right){\displaystyle \underset{\begin{array}{c}1\le j\le p^{a-m}\\ \gcd \left(j,p\right)=1\end{array}}{\sum }{\chi }_{p^a}\left(1+j{p}^m\right)}\\ +p^{ar-r}{\displaystyle \underset{m=l}{\overset{a-2}{\sum }}\left(p^m-1\right)p^{-mr}}\left(1-{\left(p^{-r}\right)}^{a-m-1}\right){\displaystyle \underset{\begin{array}{c}1\le j\le p^{a-m}\\ \gcd \left(j,p\right)=1\end{array}}{\sum }{\chi }_{p^a}\left(1+j{p}^m\right)}\end{array}$

$\begin{array}{l}=\left(p^{a-1}+p^{\left(r+1\right)\left(a-l\right)}-p^{ar+a-1-lr}-p^{a-l}\right)\\ +p^{ar-r}\phi \left(p^a\right)\left({\displaystyle \underset{m=l}{\overset{a-2}{\sum }}{p}^{-mr}}-{\displaystyle \underset{m=l}{\overset{a-2}{\sum }}{p}^{r-ar}}-{\displaystyle \underset{m=l}{\overset{a-2}{\sum }}{p}^{\left(-r-1\right)m}}+{\displaystyle \underset{m=l}{\overset{a-2}{\sum }}{p}^{r-ar}}{p}^{-m}\right)\\ =p^{a-1}-p+p^{ar+a-lr}\left(p^{-l}-p^{-1}\right)-\left(a-l-1\right)\phi \left(p^a\right)+\phi \left(p^a\right)\frac{p^{ar-lr}-p^r}{p^r-1}\\ -\phi \left(p^a\right)\frac{p^{ar-lr-l+1}-p^{r-a+2}}{p^{1+r}-1}\end{array}$

把上面关于A, B, C, D的结果加起来，化简后结果为：

$A+B+C+D=\phi \left(P^a\right){\sigma }_r\left(\frac{p^a}{p^l}\right)$ ,

所以得到了我们想要的结果。

定理1.2的证明：记 $n={\displaystyle {\prod }_{i=1}^r{p}_i^{a_i}}$ 和 $d={\displaystyle {\prod }_{i=1}^r{p}_i^{b_i}}\left(0\le b_i\le a_i\right)$ 。由定理1.1的证明，如果 $\chi$ 有分解 $\chi ={\chi }_{p_1}{\chi }_{p_2}\cdots {\chi }_{p_r}$ ，记 $g\left({\chi }_{p_i}\right)$ 是 ${\chi }_{p_i}$ 的导子，则我们有 $g\left(\chi \right)=g\left({\chi }_{p_1}\right)g\left({\chi }_{p_2}\right)\cdots g\left({\chi }_{p_r}\right)$ 且 $g\left({\chi }_{p_i}\right)=p_i^{b_i}\left(1\le i\le r\right)$ 。注意到，对于任意的模n的特征 $\chi$ ，函数 $f\left(n\right)$ 是积性的(见(4)式)。于是由命题3.1，我们有

$\begin{array}{l}{\displaystyle \underset{\begin{array}{c}1\le k,b_1,b_2,\cdots ,b_r\le n\\ \gcd \left(k,n\right)=1\end{array}}{\sum }\gcd \left(k-1,b_1,b_2,\cdots ,b_r,n\right)\chi \left(k\right)}\\ ={\displaystyle \underset{i=1}{\overset{r}{\prod }}\left({\displaystyle \underset{\begin{array}{c}1\le k,b_1,b_2,\cdots ,b_r\le n\\ \gcd \left(k,n\right)=1\end{array}}{\sum }\gcd \left(k-1,b_1,b_2,\cdots ,b_r,n\right){\chi }_{k_i}\left(k\right)}\right)}\\ ={\displaystyle \underset{i=1}{\overset{r}{\prod }}\left(\phi \left(p_i^a\right){\sigma }_r\left(\frac{p_i^a}{p_i^l}\right)\right)}\\ =\phi \left(n\right){\sigma }_r(nd)\end{array}$

证毕。

参考文献

[1]	Li, Y., Hu, X. and Kim, D. (2018) A Generalization of Menon’s Identity with Dirichlet Characters. International Journal of Number Theory, 14, 2631-2639. https://doi.org/10.1142/S1793042118501579
[2]	Apostol, T.M. (1976) Introduction to Analytic Number Theory. Undergraduate Texts in Mathematics. Springer-Verlag, New York/Heidelberg
[3]	Menon, P.K. (1965) On the Sum (a-1, n)[(a, n) = 1]. Journal of the Indian Mathematical Society, 29, 155-163.
[4]	Sury, B. (2009) Some Number-Theoretic Identities from Group Actions. Rendiconti del Circolo Matematico di Palermo, 58, 99-108. https://doi.org/10.1007/s12215-009-0010-6
[5]	Miguel, C. (2014) Menon’s Identity in Residually Finite Dedekind Domains. Journal of Number Theory, 137, 179-185. https://doi.org/10.1016/j.jnt.2013.11.003
[6]	Miguel, C. (2016) A Menon-Type Identity in Residually Finite Dedekind Domains. Journal of Number Theory, 164, 43-51. https://doi.org/10.1016/j.jnt.2015.12.018
[7]	Zhao, X.-P. and Cao, Z.-F. (2017) Another Generalization of Menon’s Identity. International Journal of Number Theory, 13, 2373-2379. https://doi.org/10.1142/S1793042117501299