1. 引言
液滴在固体表面接触后的行为是一个研究非常广泛的课题,在不同的初始状态下,会发生铺展、回缩、飞溅、反弹、破碎等现象,其中铺展是最基础的接触行为。液滴在固体表面进行铺展,通常的现象是铺展到最大直径后回缩,振荡,在粘性耗散的作用下逐渐静止。至今人们对液滴铺展的理论研究尚不令人满意,理论结果和实际试验结果有较大差别。
液滴在固体平面铺展过程中的能量转换问题,较少有人详细进行讨论。Chandra和Avedisian [1]、施明恒 [2] 认为,液滴耗散能量来源于液滴动能和表面能。廖强等 [3] 认为,两个液滴碰撞后发生震荡,其粘性耗散来源于液滴聚合后,气液界面面积的减少而释放出的表面能。秦梦晓等 [4] 认为,在液滴碰撞到固体表面时,液滴的动能转换成表面能被黏性耗散掉。王辉 [5] 认为,液滴在壁面的振荡是动能、势能、表面自由能的转换过程,并且过程中伴随能量耗散。液滴在铺展过程中,动能和势能减小,转化为表面自由能,并且伴随液滴粘性力造成粘性耗散。当液滴铺展速度降低为零时,液滴达到最大铺展并在表面自由能的作用下回缩。回缩过程液滴高度增大,速度开始增大后减小直至液滴达到最大高度,其中液滴自由能转化为势能,中间过程部分能量由于粘性作用耗散。因为粘性作用造成能量耗散,液滴振荡多个周期后能量降低为零,液滴达到静止状态。
这些讨论代表了在液滴铺展过程能量转换的普遍观点。认为液滴动能和表面能在铺展过程中进行了转化,粘性耗散的能量来源包含表面能。
本文通过模型假设,对液滴铺展过程进行简化,对铺展过程的能量转化进行了详细讨论,认为表面能并没有直接参与动能转化,也没有直接参与粘性损耗,这为纠正现有的铺展过程能量守恒方程提供了新的思路。
2. 分析模型
液滴铺展过程中与固体表面发生粘附,粘附功表征了粘附现象的自由能转换。在铺展的某个时刻,假设不改变液滴形状而将液滴剥离固体表面,需做的功应为粘附功。
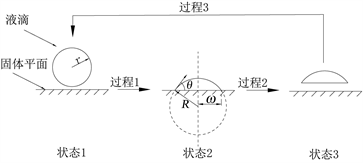
Figure 1. Hypothetical process schematic diagram
图1. 假设过程状态示意图
液滴在铺展过程中体积保持不变,体积功为零,但在表面张力的作用下发生形变,和固体类似,应有变形能存在。假设液滴为理想弹性体,其变形能应为分子势能的变化引起。
因此,如图1,可以假设一个过程,由液滴的铺展、剥离和回缩构成,液滴经过这一过程恢复原状,系统总能量应守恒。
状态1:曲率为r,密度为ρ,表面张力为γL的球型液滴,处于面积为A1,表面张力为γS的理想固体平面上方。忽略液滴和固体平面的未接触距离,设液滴的初始动能为零。此时,液滴表面积S1和体积V1为:
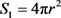 (1)
(1)
(2)
将液滴和固体平面看作一个系统,则系统的总表面能EB1为:
(3)
过程1 (铺展过程):状态1的液滴滴落在平面上,在表面张力水平分力的作用下逐步铺展。
状态2:铺展的某一时刻,形成接触角为θ,铺展半径为ω,铺展面积为A2的球缺状液滴,该球缺的曲率为R,则状态2时,液滴表面积S2、体积V2和铺展面积A2为:
(4)
(5)
(6)
固液表面张力为γLS,忽略三相接触线线张力,忽略饱和蒸汽压的变化导致的系统化学势的变化。系统的总表面能EB2为:
(7)
铺展过程中,固液界面产生粘附,能量变化值等于粘附功WN:
(8)
假设在铺展过程中液滴的密度ρ保持不变,由质量守恒定律可知V1= V2,即:
(9)
过程2 (剥离过程):假想将铺展后的球缺状液滴脱离固体平面,但保持形状不变。根据热力学第一定律可知,此时系统内能的变化等于粘附功,因此可以认为在状态2时,系统在固液界面上储存了相当于粘附功的能量,记为粘附能EN= WN。
状态3:过程2形成的液滴系统的总表面能EB3为:
(10)
过程3 (回缩过程):球缺状液滴在表面能的作用下收缩成球状,恢复到状态1,此时系统的总表面能EB4= EB1。状态3的表面能恒大于状态1,过程3中表面能逐步减小。对液体变形能而言,无限平面液滴内部变形能最小,球型液滴的内部变形能最大,因此,在过程3中,液滴的变形能在逐步增加,其变形能EX满足:
(11)
3. 表面能
由式(3) (7) (8)和(11)联立,并EX2= EX3,或建立各过程的能量守恒方程,均可得:
(12)
考虑到液滴铺展过程是由于表面张力在水平方向分力引起,其功WB1为:
(13)
根据杨氏方程,平衡接触角θP满足:
(14)
将式(6) (9) (14)带入(13)并整理得:
(15)
因此在铺展过程中,表面张力的水平分力做功是引起系统的表面能变化的根本原因。当接触角θ = θP时,式(15)可简化为(RP为液滴的平衡曲率):
(16)
考虑到表面能、粘附能和变形能均为内能,从式(12)、(15)可知,在液滴铺展过程中,系统的内能(分子动能除外)守恒,在表面张力水平分力的驱动下,系统的熵增加,液滴表面能和变形能转化为粘附能,没有多余的表面能参与粘性耗散。
进一步分析,可以认为,在液滴的铺展过程中,表面张力的水平分力对液滴动能没有贡献。在常规的认识中,如崔正刚 [6]、陶英 [7] 等认为,表面张力是液滴铺展的动力。在铺展过程中,表面张力的水平分力的合力为:
(16a)
根据杨氏方程,当接触角θ小于平衡接触角θP时,合力F应大于零,根据牛顿运动定律可以推论,液滴的铺展速度应随着时间增大,当接触角等于平衡接触角时,铺展速度达到最大。但这一推论和大多数的试验结果相违背。李大树 [8]、李德伟 [9] 等在试验中均指出,液滴在第一振荡周期内的铺展速度均随时间下降。这从侧面给出了表面张力的水平分力没有参与液滴动能的证据。
4. 压力能
铺展过程中,液滴的内能守恒,液滴的铺展动能就只能来源于同属机械能的压力能和重力势能。将液滴视为不可压缩流体,忽略液静压,由于液滴具有曲率,并符合拉普拉斯方程,同时,液滴在铺展过程中体积保持不变,因此:
状态1时,液滴的附加压力能EY1为:
(17)
状态2时,液滴的附加压力能EY2为:
(18)
在铺展过程中,液滴表面张力在垂直方向的分力作用在三相接触线上,并对铺展面A2形成压力,在数值上等于拉普拉斯压力 [10] ,因此滴液表面张力的垂直分力在铺展过程中做功WB2应等于拉普拉斯压力做功,即等于压力能差:
(19)
另外,结合式(16),在液滴铺展完成时,表面张力做的总功WB为:
(20)
5. 粘性损耗
在不考虑其他能量损失,如固液界面的摩擦、三相线阻力等时,液滴铺展的能量损耗只来源于粘性损耗。从粘性损耗的定义来看,粘性损耗的直接能量来源仅为机械动能,其他形式的能量只有先转化为动能后,才可能产生粘性损耗。在忽略液滴势能、静液压能等其他机械能转化为动能的情况下,粘性损耗能量Wφ应等于压力能差,并和表面张力的垂直分量做功平衡:
(21)
在目前的研究当中,液滴铺展过程的粘性耗散能,大都使用式(22)进行计算 [1] [11] [12] ,是不正确的,方程中不应含有表面能,而应含有压力能。
(22)
6. 结论
1) 液滴铺展过程中,内能守恒,表面能、粘附能和变形能相互转化,没有参与粘性耗散;
2) 粘性耗散的主要能量来源于压力能;
3) 表面张力的水平分量做功引起了内能的转化,垂直分量做功引起了粘性耗散。
参考文献