1. 引言
排队论主要研究各种排队系统在排队等待中的概率特性,应用领域非常广泛,国内外学者针对不同的排队模型做了大量的研究。Ward通过奥伦斯坦–乌伦贝克过程,得到了稳态下单服务台队列的扩散逼近 [1] 以及负荷过程和队长过程的收敛极限 [2] 。文献 [3] [4] 研究了高负荷下单服务台队列的队长和溢出过程的极限。在高负荷条件下,Liu等研究了到达率随时间变化的网络队列模型 [5] ,Whitt研究了到达临界点的单服务台队列 [6] 。另外,Ma [7] 和Dong [8] 分别对单服务台和多服务台的周期到达队列模型做了一定的研究,并对模型进行数值模拟,更加直观地验证了所得结论。Baccelli等 [9] 和Stanford [10] 在平稳状态下研究了一个服务台的队列性能,得到了有关数量分布的积分方程。本文在前人研究的基础上,运用中心极限定理以及连续映射定理等 [11] [12] 相关知识,研究到达率随时间变化的Gt/Gt/1队列模型,得到队列模型的各种性能指标(到达过程、队长过程和虚等待时间)的收敛极限。
2. Gt/Gt/1队列模型
考虑一般的单服务台Gt/Gt/1队列模型,假定等待空间无限,到达率随时间变化,到达率为
,服务率为
,负荷强度为
。A表示到达计数过程,
表示累积到达函数,当
时,
,
到达率满足:
,
在不考虑顾放弃的情况下,假设
。
到达过程满足:
,
其中
是随机计数过程,满足泛函强大数定理(FSLLN)和泛函中心极限定理(FCLT),即当
时,在D空间中,
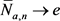 ,
,
,
,
这里
,
,e是恒等函数,
,
是标准的布朗运动。
另外,假设服务是由随机计数过程
(独立于
)产生的,
同样满足泛函强大数定理(FSLLN)和泛函中心极限定理(FCLT),即当
时,在D空间中,
,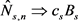 ,
,
这里
,
,
是标准的布朗运动,且独立于
。
3. 主要结论及讨论
考虑一系列模型中的第n个模型,下面建立与到达过程有关的高负荷极限,对于单服务台的高负荷极限,通常使负荷强度逐渐趋于1,这里当
时,令
。当
、
时,对到达函数
和累积到达函数
进行流体刻画,分别为:
,
.
则有
。
另外,为了后续研究的方便,对累积到达函数
在时间
通过增量
进行刻画,即
,当
时,有:
,
,
.
假设在D空间中,当
时,
,
。
累积到达函数
的扩散刻画如下
,
假设
,
为连续函数。
到达过程满足:
,
根据以上到达函数的刻画,接下来对到达过程进行刻画,如下:
,
,
,
,
.
定理1 (到达过程的极限):在以上刻画的前提下,在D空间中,当
时,
有如下的泛函强大数定理:
。
以及泛函中心极限定理:
,
.
证明:根据文献 [11] 中13.2以及连续映射定理,
且由
,
,得
,
又由
,
,得:
由
,以及胎紧性,有:
,进而得:
接下来刻画队长和虚等待时间:
当
时,
,
。
是漂移系数为a,扩散系数为b的反射布朗运动。
定理2 (虚等待时间的高负荷极限):假定系统开始为空,在以上刻画的基础上,且满足以上到达函数,则在
空间中,当
时,有
,这里当
时,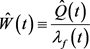 ,
,对于每一个
,
,对于每一个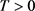 ,当
,当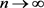 时,
时,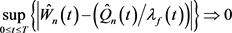 。
。
证明:首先刻画到达和服务过程,当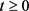 、
时,
、
时,
,
,
所以当
时,在 空间中,
空间中,
,
其中
和
是相互独立的布朗运动,
因此在D空间中,
,
其次应用 [11] 中的定理9.3.4以及连续映射定理,当
时,得:
,且
。
代表第n个系统中的离去过程,
,
其中
。
在D空间中,当
时,
。
是
时间内忙的服务台。
,
根据
以及 [11] 中的定理9.3.4,可得:
,
由
,
得
。
由
,及
,
,得:
对于每一个
,当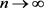 时,
.
时,
.
由联合极限以及 [11] 中的定理11.4.7,得:
在
空间中,当
时,有
。
4. 总结
在给定Gt/Gt/1队列模型的到达率函数的基础上,利用泛函中心极限定理、连续映射定理等得到该模型的到达过程、队长过程和虚等待时间的收敛极限,最后运用概率测度收敛和随机过程极限的知识对此做了证明。
参考文献