1. 引言
在航空发动机研制中,都会按要求开展可靠性累积试车、全寿命试车等试验。这些试验一般长达几百小时。在试车过程中,因杂质和污垢、叶顶间隙增大、旋转部件长时间工作在高温高压恶劣的环境中以及叶片表面粗糙度增加等原因导致部件性能衰退 [1] ,从而引起发动机性能衰减,主要表现为发动机推力下降和耗油率增加。在不采取任何维修措施的情况下,发动机性能衰退程度会进一步加重,甚至产生更为严重的后果 [2] 。为保证发动机试验安全,可根据已有的试验数据对发动机的技术状态进行预测分析,进一步降低风险。
针对发动机性能预测,目前比较成熟的方法是线性回归、时间序列预测等传统解析方法以及近年来出现的神经网络、支持向量机等人工智能算法 [3] [4] 。传统预测方法理论成熟,能够给出预测公式,计算速度快,适合做线性问题的短期预报,但对非线性问题存在局限性。神经网络用于非线性预测获得了较成功的应用,对非线性问题具有较好的预测,但发动机训练样本数量一般较少,数据非线性程度高,单一的BP神经网络模型预测精度不高,而且神经网络模型存在一些不可避免的缺陷(如容易陷入局部最小、过拟合等) [5] [6] [7] [8] 。通过文献 [9] 可知,发动机性能衰减预测技术的研究,大都以发动机推力、排气温度或者反映发动机性能的综合指标参数进行预测。
考虑到推力是直接反映发动机性能衰退的最直接参数,本文以发动机推力作为性能状态衰减分析的预测参数,以某航空发动机累积试车试验数据为样本,针对发动机试车数据特点,发动机推力衰减过程存在线性趋势变化成分和非线性剩余量两种成分,结合两种算法的不同特点,建立ARIMA-BP组合分析模型,以此来预测发动机推力变化趋势。同时将预测结果与ARIMA模型的预测结果进行比较。结果表明,组合模型的预测精度有所提高,对发动机试车安全具有一定的参考意义。
2. ARIMA-BP神经网络组合预测模型
2.1. ARIMA模型
ARIMA (Autoregressive Integrated Moving Average Model)模型全称为自回归移动平均模型,一般形式为ARIMA(p, d, q),其中p是自回归模型的阶数,d为时间序列形成平稳序列时的差分次数,q是移动平均的阶数。ARIMA方法将非平稳时间序列转化为平稳时间序列,能够在数据模式未知的情况下找到适合数据考查的模型 [10] 。
ARIMA模型结构为 [11] :
(1)
(2)
(3)
建立ARIMA时间序列模型的基本步骤 [12] :
1) 数据预处理。通过对序列进行平稳化检查,判断时间序列是否为平稳序列,若为非平稳序列,通过差分变换、对数变换等方法,使其平稳化;
2) 模型识别。模型识别主要是通过时间序列的自相关函数(ACF)、偏相关函数(PACF)的图形进行分析把握模型的大致方向,初步确定p、q的值,利用AIC准则、BIC准则等方法对多种模型进行对比和筛选,确定最优的模型参数;
3 )模型估计。参数估计检验是否具有统计意义;
4) 模型假设检验。诊断残差序列是否为白噪声序列,若残差序列不能近似为一个白噪声序列,则需要再次对模型进行识别;
5) 模型预测。利用已通过检验的模型进行预测分析。
2.2. BP网络模型
人工神经网络有许多模型,在实际应用中采用多层网络的误差反向传播学习算法,即BP(Back Propagation)神经网络。BP网络是单向传播的多层前向网络,主要特征是信号前向传递,误差反向传递,可以根据目标误差的大小反馈到中间层,根据误差大小对权值矩阵进行反馈修改。BP神经网络实现从样本输入到目标输出任意精度的非线性映射,它在函数逼近、模式识别、曲线拟合等方面得到广泛应用。
BP神经网络包括输入层、隐含层和输出层三个层次。其中,输入层和输出层只有1层,而隐含层为多层。BP神经网络结构如图1所示,其中,x 代表网络的输入,y 代表网络的输出,w 代表输入层神经元和中间层神经元之间的权值,v 代表中间层神经元和输出层神经元之间的权值。由图1可以看出,BP神经网络可以看成一个非线性函数,网络输入值和预测值分别为该函数的自变量和因变量。当输入节点

Figure 1. The typical architecture of BP neural network
图1. 典型BP神经网络结构
数为n、输出节点数为m时,BP神经网络就表达了从n个自变量到m个因变量的函数映射 [13] 。
BP神经网络训练过程包括:网络初始化、隐含层计算、输出层计算、误差方向传播计算、权值更新、阀值更新等。各参数设计如下:
1) 输入层和输出层的设计。输入节点数取原始数据的维数,输出节点数取输出数据的维数;
2) 隐含层层数设计。最多需要两个隐含层;
3) 传递函数设计。隐含层传递函数一般选择logsig或tansig函数,输出层传递函数一般选择tansig或purelin函数;
4) 隐含层节点数设计。根据经验公式:
(4)
式(4)中,I为隐含层节点数;n为输入节点数;m为输出节点数;
为1~10之间的随机常数。用同一样本训练BP网络,当得到的误差最小时,进而确定对应的隐含层节点数I。
2.3. ARIMA-BP神经网络组合模型
航空发动机是一个非常复杂的非线性系统,发动机推力性能退化过程通常是一个非线性、非平稳性的时间序列,ARIMA模型能够很好的提取时间序列数据的整体变化趋势,而BP神经网络能够提取出时间序列数据的非线性特征,充分发挥ARIMA模型和BP神经网络模型的优势,其组合模型能很好的预测发动机性能变化趋势。
ARIMA-BP组合模型预测流程见图2。
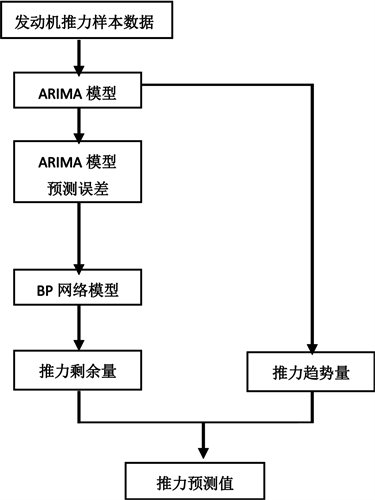
Figure 2. Prediction flowchart of ARIMA-BP combined model
图2. ARIMA-BP组合模型预测流程
ARIMA-BP组合模型预测步骤如下:
1) 将发动机推力样本数据分为两类:一种是训练样本,用于建立ARIMA和BP两种模型;另一种验证样本,用来验证模型;
2) 根据发动机推力训练样本建立ARIMA模型,进而得到推力趋势预测值;
3) 利用推力真实值与趋势值之差得到推力拟合误差;
(5)
式中,
为t时刻ARIMA模型的预测值。
4) 将ARIMA模型拟合误差
作为BP网络的输出,推力趋势预测值
作为BP神经网络的输入,训练BP神经网络模型。根据建立好的BP模型进行预测,得到推力预测误差修正值
。
5) 推力预测误差修正值和推力趋势预测值相加,得到推力变化预测结果。
(6)
式中,
为t时刻ARIMA-BP组合模型的预测值。
3. 组合模型预测及结果分析
3.1. ARIMA模型预测
航空发动机试验中,很难获取发动机在不同状态的推力数据,某些状态参数较少甚至没有样本参数,难以建立预测模型对发动机在不同工作状态下的推力数值进行预测。本文选取某型涡扇发动机累积试车数据为分析对象,以试车循环为一个周期,共35个循环的试车数据,统计每个试车循环中发动机最大推力数据进行建模,分析发动机推力的变化趋势。以前30个循环发动机推力数据进行训练,后5个循环进行短期预测分析。
绘制发动机推力序列图,可以看见性能趋势呈衰减趋势,具有明显的非平稳性。对序列进行差分处理,一阶差分后的自相关图和偏相关图如图3所示。
由图3可知,自相关图和偏自相关图均表现出拖尾现象,适用于ARIMA模型。偏自相关图和自相关图均在置信区间内,趋于0,呈拖尾现象,初步判断p值和q值取0或者1,序列进行一阶差分处理,d取值为1。利用SPSS软件,运用BIC准则进行定阶。计算出不同模型的BIC值,选取BIC达到最小的一组阶数为最优。通过SPSS软件的参数评估,最后选取ARIMA(1, 1, 0)模型最为合适。
对建立的发动机推力衰减预测模型ARIMA(1, 1, 0),得到残差的相关函数见图4。
由图4可以看出残差的自相关图和偏相关图都没有显著的趋势特征,且残差序列的自相关和偏自相关系数大多接近于零,这表明残差序列已经达到白噪声。因此,可知ARIMA(1, 1, 0)模型是合理的。
3.2. ARIMA-BP组合模型预测分析
ARIMA(1, 1, 0)模型得到推力趋势预测值后,将预测的推力趋势预测值作为输入,模型拟合值与样本推力值的残差作为BP神经网络的输出参数,从而得到推力剩余值。按照2.2节介绍的神经网络设计方法,训练函数为trainlm函数,隐含层传递函数为tansig函数,输出层传递函数为purelin函数,按照经验公式(4)经反复测试,确定隐含层节点数为10,学习率0.3,目标误差为0.001,最大迭代步数3000,得到ARIMA-BP组合预测模型。
对于预测问题,为了更好的对模型精度进行比较,通常使用均方误差(MSE)和平均绝对误差(MAE)2种指标进行评价,计算式分别为:
1) 均方误差(MSE)
(7)
2) 平均绝对误差(MAE)
(8)
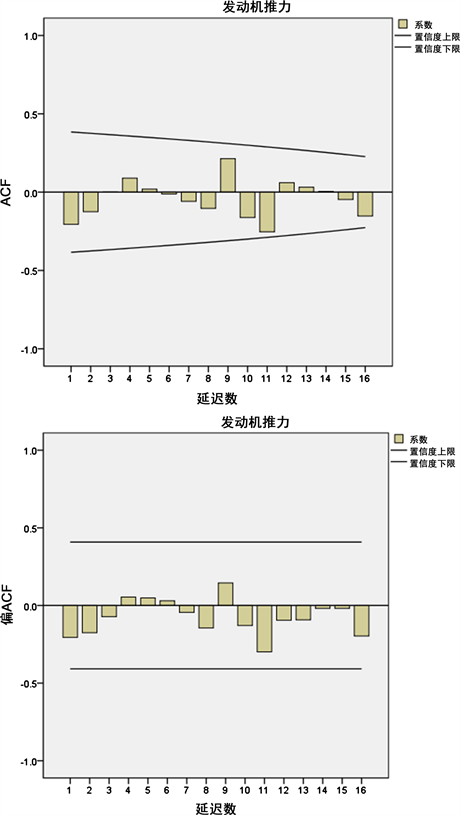
Figure 3. The ACF and PACF diagrams after one-order difference
图3. 一阶差分后自相关和偏自相关图
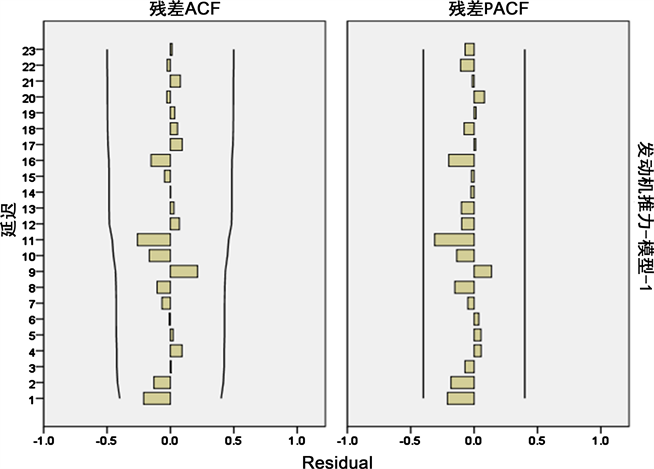
Figure 4. The ACF and PACF of residual errors
图4. 残差的自相关和偏相关图
分别进行计算,得到ARIMA模型、ARIMA-BP组合模型、SVM的均方误差(MSE)和平均绝对误差(MAE)见表1。由表1可以看出,组合模型的均方误差和平均绝对误差值均低于直接的ARIMA模型的指标值,可见组合模型的预测精度较高,这对航空发动机这样复杂系统的性能预测尤为重要。

Table 1. Calculated results of MES and MAE
表1. 均方误差和平均绝对误差计算结果
由表1可知,ARIMA-BP组合模型精度优于ARIMA模型,略好于SVM预测模型,主要因为ARIMA模型只是预测出推力平稳的变化趋势,不能反映推力中非线性的变化成分。而组合模型可以预测平稳趋势和非线性变化成分,SVM模型虽然有较高的预测精度,但要求预测模型结构复杂,算法中的关键参数不易寻找,且受样本数据的形式(疏密性、非线性等)影响较大。因此组合模型可以用于发动机台架试车性能衰减的短期预测。
经过计算可知,第36个试车循环,预测的发动机推力比设计点的推力衰减约8%。若定义该型发动机性能衰减的阀值(如推力衰减不超过5%),此时根据预测结果应对发动机作相关处理。如清洗发动机流道,核心部件孔探检查等,在对发动机进行必要的安全检查以及处理后,再决定是否进行下一个循环的试车,这样能极大提高发动机试车安全。
4. 结论
针对发动机台架试车性能衰减短期预测分析的问题,本文建立了ARIMA-BP组合预测模型。论述了该模型的设计方法与步骤,并与ARIMA模型的预测结果进行了对比。结果表明,组合模型预测精度更高,平均绝对误差为0.615。该模型可以有效预测发动机性能衰减变化趋势,提前预知发动机的性能状态,为确保发动机试车安全提供了一种可行的方法。