1. 引言
近年来,随着Web 2.0技术的迅猛发展,各类在线社交媒体(Online Social Medias)如雨后春笋般的不断涌现。特别是随着移动互联网技术的普及,众多社交媒体开始推出一种新型的“基于事件的社交网络服务”(Event-based social networks,EBSNs) [1][2][3],例如国内的豆瓣,国外的Meetup,Plancast和EventBrite等。在此类服务中,事件组织者在社交媒体平台上发布社交事件的时空信息(如事件的召集地点和事件的举办时间) [4]和事件的属性等,接着社交媒体平台会推送不同社交事件给可能的潜在参与者。总之,基于事件的社交网络平台主要是把线上的用户和线下的事件关联在一起,它在推送线上事件给潜在用户的同时,衍生出活动的计划或安排、活动的推荐、活动的预测等社交服务。本文出现的“活动”即为社交网络中的“事件”,即“事件”与“活动”一词通用。
传统的社交网络,大多用户只是在线上平台上互动,很少在线下见面交流,而基于事件的社交网络与基于位置的社交网络有点类似,基于位置的社交网络 [5]是由用户活动的地理位置、在线上社交媒体分享的内容信息以及它们之间的关联性构成;而基于事件的社交网络由线上社交网络和线下社交网络构成,线上社交网络指的是用户通过大量信息交流、传播等连接关系构成的交互结构,线下社交网络指的是用户根据活动的信息参加活动的交互关系。总之,基于事件的社交网络服务不仅提供一个虚拟的环境让用户互相交流想法和分享经验,同时通过在真实世界参加活动时获取面对面的互动机会 [6]。因为基于事件的社交网络在线上线下都有交互活动,这就是区别于仅仅在线上有交互活动的传统社交网络和其他的网络服务。图1是基于事件的社交网络的结构图(Meetup),两个用户在线上同时加入一个群组,在线上社交网络有交互活动,而在线下他们不一定是好友,但是他们可能会在线下参加同一个活动或者参加不同的活动。这样由线上线下网络构成的社交服务类型即本文即将要论述的基于事件的社交网络。近年来,基于事件的社交网络越来越普及,有数据表明在2015年1月份的第一周,Meetup注册了3000个群组,33万个用户 [3];此外,Eventbrite自2012年发展至2016年1月份,每周约有200万用户在上面购买活动门票 [7]。
基于事件的社交网络服务研究的重要性使得众多研究者们提出各种预测、推荐和活动计划或安排的

Figure 1. Event-based social networks [2]
图1. 基于事件的社交网络 [2]
方法 [8],让用户在线上线下交互中得到较佳的体验,它在组织者的影响力分析、信息传播和分享经验等应用中具有重要价值。其中,预测和推荐是社交网络的经典问题,而活动计划和安排是基于事件的社交网络的主要问题。另外,基于事件的社交网络不仅具有传统的社交网络的虚拟性、移动性 [9]和社区化 [10]等信息服务特征,而且能够根据不同用户的个性化需求进行活动的计划,推荐以及预测等,在国内外逐渐赢得了广泛关注,许多大学和研究机构对此研究领域展开了深入讨论。其中,国际重要会议和期刊也频频出现了很多有关基于事件的社交网络服务数据管理技术的重要研究成果,例如KDD [1][2][11]、VLDB [12]、SIGMOD [13][14][15]、ICDE [16][17]、AAAI [18]、TKDE [19]、RecSyc [3]。它们主要讲述了基于事件的社交网络的活动计划、预测、活动推荐和活动组织者影响最大化等,以及探讨了线上网络与线下网络交互 [20]的研究进展以及遇到的问题。而本文也是从组织者影响最大化、多特征混合和亲密度最大化来论述预测问题;从用户最优策略、最大–最小化和活动冲突的方法来阐述活动计划或安排问题;此外,还从基本假设的不同给推荐方法分类。
本文针对基于事件的社交网络数据管理技术目前已有的研究成果与应用进展进行综述。第2节着重介绍基于事件的社交网络的问题、相关特征以及数据集;第3节主要介绍基于事件的社交网络服务预测问题的方法;第4节从用户参加的活动个数来给活动计划或安排的方法进行分类,并对其详细论述;第5节是针对推荐问题的现状进行分析;第6节给出了本文的总结和发展趋势。
2. 基于事件的社交网络
传统的线上社交网络服务 [21],如人人网、开心网等逐渐没落,而基于事件的社交网络服务,如国内的豆瓣、国外的Meetup、Plancast等却正以惊人的速度向各个领域蔓延。基于事件的社交网络因其特有的线上分享交流、线下用户根据自己的地理位置、兴趣爱好和行为特征等属性参加活动在社交网络中发挥了重要作用 [22]。本节首先概述基于事件的社交网络服务的问题,然后对基于事件的社交网络的特征及数据集进行阐述。
2.1. 基于事件的社交网络的问题描述
基于事件的社交网络如图1所示,它由线上网络和线下网络组成。用户不需要物理实际网络的接触就可以在线上网络进行互相交流、分享经验、共享相片等信息服务,用户同时还可以通过线上网络的评论、参加的活动获知他的“追随者”。此外,用户通过实际物理空间信息的接触可以在特定的时间和特定的地点参加同一个活动 [2][9]。其中,线上社交网络 [23][24]和线下社交网络 [25][26]都不是一种新型的社交网络,但是这两者的结合即构成了一种前所未有的社交网络,即基于事件的社交网络服务。
本文从预测、推荐以及活动的计划或者安排来论述基于事件的社交网络数据管理,预测是根据活动组织者的影响力、用户参加过的活动记录以及用户对活动的兴趣程度等信息进行预测活动的潜在参与者;推荐是依据线上用户所居住的地理位置到事件召集地点的距离、线上用户对线下活动的兴趣程度以及线上用户之间的友好关系等信息给线上用户推荐相关活动或者推荐路径行程 [83];活动的计划或者安排是结合线上用户注册的信息给其安排线下的活动或者规划行程路径等服务 [80]。从实体上来讲,预测、推荐和活动计划或安排的作用都是用户、活动、用户标签和活动标签等;从影响用户和活动的因素来讲,预测、推荐和活动计划或者安排都与用户到活动的距离、对活动的兴趣程度和用户的社交关系有关;从方法上来讲,预测与计划或安排都用了亲密度最大化的方法,预测与推荐都用了多特征的方法,而计划或安排在最大–最小的方法上也是用了多特征混合的方法;从应用上来讲,预测是给活动预测潜在的用户,推荐是给用户推荐活动或者行程路径;活动计划或安排是给用户计划或者安排活动、行程路径等,无论是哪一个角度来讲,预测、推荐和活动的计划或安排有交集的部分,也有不同的部分,因此这三者的关系如图2所示。
2.2. 基于事件的社交网络的特征及数据集
基于事件的社交网络不仅包含许多互相关联的个体,而且还对网络虚拟化的关系现实化,它实现了虚拟的社交关系和真实物理空间活动的信息共享 [6]。基于事件的社交网络是在传统的社交网络服务的基础上,进一步增加了用户到召集活动的距离、活动的举办时间、用户的兴趣爱好、用户的标签以及用户在线上社交网络所加入的群组等各种知识。但是,值得引起大众关注的是,在线上社交网络加入同一个群组的用户,他们在线下社交网络并不一定会一起参加同一个活动。用户参加的活动取决于多方面知识的综合,其中包括用户的标签,用户所住的地点到举办活动地点的距离,活动举办的时间,用户对活动的兴趣程度以及该用户的社交关系等信息都是决定用户是否参加某个活动的关键因素。
此外,基于事件的社交网络还有其他的特征,如异质的社会关系(Heterogeneous social relationships),地理信息(geographical information)等。异质的社会关系指的是线上线下之间的交互关系 [27],线上社交服务的特征反映线上交互关系,而线下社交关系的特征是通过事件服务来反映的。
基于事件的社交网络主要包括以下几种数据集:1) 来自Meetup的数据。在Meetup上,用户创建一个活动的时候,会涉及到群组的标签、活动的时间、地点以及活动的属性。其他的用户可以在网上表达他们对这个活动的意愿“参加”、“不参加”和“可能参加” [2]。为了促进用户线上的交流,Meetup允许用户在线上建立互相评论、分享相片和活动计划的群组。假设用户ui和用户uj加入线上社交网络Gon的同一个群组,gr表示一个群组,它有|gr|个成员。如果存在一个gr,有
并且
,则
,其中Aon是线上交互关系,用ek来表示线下社交网络的任一事件。文献 [2]用了一个相似的方法 [28]来定义线上社交网络交互的边的权重:
(1)

Figure 2. Classification of event-based social networks
图2. 基于事件的社交网络的分类
同理,线下社交网络边的权重可以表示为:
(2)
2) 豆瓣数据。该数据集记录了五个信息:活动的地理位置、活动的举办时间、活动的出席者、活动的组织者以及活动的内容 [29]。
3) Gowalla数据集。Gowalla是一个非常有名的基于位置的社交网络服务,它记录了用户在不同时间点上所处的地理位置点 [2],通过用户登记的地点信息来表示用户的标签。
总体来讲,相比于其他网络数据集(例如传统的社交网络数据集、基于位置的社会化服务的数据集),基于事件的社交网络数据集有如下几个特点:
1) 网络交互。基于事件的社交网络由线上社交网络和线下社交网络组成,它打通了线上虚拟世界与线下真实物理世界的渠道,将线上虚拟世界的交流转换到现实社会的接触,这使得基于事件的社交网络的用户行为同时具备了虚拟化、生活化、时间动态性以及空间动态性等特征,形成了由线上用户交流、评论、分享等社交行为的网络服务和线下在指定的地理位置、特定的时间段参加同一个活动的社交网络,使得用户在线上网络与线下网络得到很好的交互。
2) 活动的特征。一般来说,活动的地理位置信息、活动举办的时间点以及活动的内容是用户首要关注的事项。一群用户会在指定的地点指定的时间段参加一个特定的活动,这也是区别于基于位置的社交网络的重要信息。在决定是否参加这个活动之前,有些用户会关心活动的组织者,如果一个组织者是用户所熟悉的人,用户就会比较信任这个组织者,于是就会召集自己的朋友也来参加这个活动。
3) 明晰的社会关系。用户在线上社交网络的社会关系从公式(1)得出,用户在线下社交网络的社会关系从公式(2)得出,并且线上的友好关系和线下的好友关系是可以互相转换的 [20]。但是在传统的社交网络中,用户间的社会关系必须由复杂的数据中提取。
4) 群组。多个用户在线上社交网络共同评论一条新闻、讨论同一个活动、分享相片等,这些有着共同行为特征的用户会形成一个群组。一个用户可以加入多个群组,同时一个群组也包含多个用户。
3. 预测问题
基于事件的社交网络的预测问题是用户在线上社交网络服务平台发布活动之后,社交媒体平台会根据活动的举办时间和地点、组织者和活动的属性等预测活动的潜在参与者。此外,除了预测活动的潜在参与者,也会预测用户参加的活动。用户会参加什么活动,大多是由用户的兴趣爱好、用户到活动的距离以及活动本身的属性等信息决定的 [22]。
3.1. 预测问题的定义
基于事件的社交网络的预测指的是依据用户的标签、活动的属性、活动举办的环境以及朋友的社会关系等来推测活动的潜在用户和预计用户即将参加的活动。值得关注的是,很多研究者首先会把用户居住地到召集活动的距离作为预测活动参与者的关键要素 [2],活动的内容 [29]、用户对活动的兴趣程度以及组织者影响力是次要因素 [15]。但是每个用户关注的信息不同,因此对每个用户考虑的特征也是千差万别,所以要对用户进行一套统一的预测模型是非常有困难的。
此外,活动举办的时间周期也会影响到预测活动的潜在用户,例如一些用户喜欢参加周末早上的活动,而另外有些用户喜欢参加周五晚上的活动,如何做到预测哪些用户参加哪个时间段的活动 [3],就成为预测问题的难点所在。如果能把握住用户细微差别的特征,则预测给用户的活动会更符合用户的满意度,用户接受率也会越高,其体验效果会更佳。很多研究者综合上述的问题定义及其特征给出了基于事件的社交网络活动预测问题的方法。
3.2. 预测问题的方法
基于事件的社交网络服务预测问题是依照一定的方法对未来用户参加的活动和活动的潜在参与者进行测算。从实体类型的角度来看,主要包括用户或活动(含特定标签、群组或属性)。从模型角度来看,目前,基于事件的社交网络预测的研究方法以组织者的影响最大化、多特征混合和亲密度最大化方法为主。
3.2.1. 基于组织者影响最大化的方法
基于组织者影响最大化的预测方法主要是看组织者是谁,该组织者对群组的影响力。比如某个活动组织者之前举办过一些活动,然后影响力很好,接着再次举办其它活动的话,那么就会有很多用户基于此组织者的信誉度而报名参加其组织的活动 [31]。Yu等人 [32]认为用户会根据组织者的信息来决定是否参加活动,即用户依据组织者历史记录的信誉度来决定加入的群组或者参加的线下活动。例如豆瓣社交网站 [33]上面会有活动的相关信息,如活动的组织者,活动举办的时间、地点,内容,已报名的用户。在未来即将到来的用户,如果用户看到是自己熟悉的组织者或者是自己崇拜的偶像组织的活动,那该用户会以很大的概率加入该组织者的群组或者报名参加该组织者召集的活动。
Feng等人 [15]根据组织者影响最大化的方法来寻找一个活动潜在的最大用户数,先前也有研究团队给出了影响最大化的研究 [34]- [41],但是基于事件的社交网络数据管理的组织者影响最大化与传统的影响最大化 [42][43]有本质的区别。Feng等人是结合了线上线下的社交网络来考虑线下活动组织者的影响最大化,即给出一张线上社交网络图G,图上的顶点表示用户,每个用户v有一系列的相关属性A(v),用ai Î A(v)表示用户v具有属性ai,在这里的属性可以代表一个用户的兴趣爱好。如图3(a)所示,有一张社交网络图,图上有四个顶点代表四个用户u1,u2,u3,u4,每个顶点旁边的即是用户的属性A(u1) = {a, b, c},A(u2) = {a, b},A(u3) = {c, d},A(u4) = {a, b},给定一个属性a,目的是要找到对属性a感兴趣的所有用户,此模型是能找到最多的用户越好,因此在这个例子上含有属性a的用户是{u1, u2, u3}。回到基于事件的社交网络的预测问题上,活动发布者要求参加的用户对活动感兴趣之外,在活动没有人数限制的情况下,组织者当然是希望用户来得越多越好。如果该组织者很有影响力,那么对该活动感兴趣的用户自然会来得比较多。Feng等人把这个问题类比到集合覆盖问题,集合覆盖问题是经典的NP-hard问题 [86],并且此问题在用户数增加到一定数量时,在线性时间内是找不到含有指定属性的全部用户数,由此可知这个问题是NP-hard问题。Feng等人针对此问题提出了三个算法,它们分别是贪心算法、基于划分的影响集合覆盖(Partition-based Influential Cover Set,简称PICS)和PICS的优化算法(PICS+),其中贪心算法没有近似比,它的时间复杂度为
;PICS算法的近似比为2,它的时间复杂度为
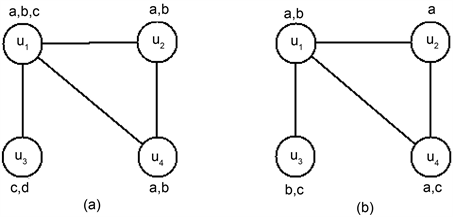
Figure 3. Social relations and user attributes
图3. 社交关系及用户属性图
。其中n是社交网络的顶点,即用户的数量;t(n)表示计算一个用户的传播影响力所需要的时间;Q是属性的集合;VQ是用户v的部分属性的候选集合;k是一个给定的整数。后两个算法涉及到划分,即给出一系列的属性Q,一个正整数k,当满足下列三个条件时: ① 对于每一个
,属性集
,并且非空; ② 对于
,
; ③
。则有
,给定两个属性集合Q1和Q2,并且
,假设P’是Q1的一个划分,P’也是Q2的一个划分。回到例图3(a)中,属性集合
,正整数k = 3,有
是一个划分;
是一个划分;
不是一个划分,因为
;
不是一个划分,因为元素c不在里面;
不是一个划分,因为p5的集合个数大于3。
3.2.2. 基于多特征混合的方法
基于多特征混合方法是研究用户和活动相关因素的重要性、将影响因素表示成特征、利用抽取的特征训练模型,最后基于这些重要的相关特征对活动潜在用户进行有效的预测等 [44]。一般来说,预测问题最后会通过大量的已知数据训练出多特征混合模型对未知信息进行预测,然后用分类模型针对因素的重要程度分为几个等级。这类预测方法的本质问题是针对用户和活动的信息影响因素进行分析,主要的操作是特征的选择与表示。目前,常用的特征主要有以下三类。
1) 活动内容
活动内容是决定用户是否会去参加某一个活动的重要因素 [45][64],一般是利用用户参加过的活动与即将举办的活动进行一个相似度的计算。如果相似度比较大,则认为该用户参加这个活动的可能性比较大,如果相似度较小,则认为用户以较小的概率去参加即将到来的活动。Du等人 [29]使用隐含狄利克雷分布(latent dirichlet allocation,简称LDA)主题模型 [46],此模型被广泛应用于社会媒体用户文本兴趣建模任务,在LDA的基础上Du等人首先对文本进行处理(去掉停用词和标点符号),接着使用吉布斯采样(Gibbs sampling),然后利用Jensen-Shannon (JS)距离 [47]来计算用户参加历史活动与即将参加的活动的相似度,为了得到更好的主题数,最后用了聚类的方法。其中主题数的选取是依据LDA的边缘分布(marginal distribution)而得,边缘分布可表示为:
(3)
其中,
是在给定的
参数依据狄利克雷分布而得到
的概率,
是在给定主题T(i),参数是
情况下,求得W(i)的概率;用JS距离求两个主题的相似度,JS的距离公式为:
(4)
(5)
其中,p,q为两个分布。例如有两个活动a1:“drama British Shakespeare classic Macbeth”、a2:“British Shakespeare King Lears”,其中a1是用户参加过的活动,而a2是用户即将要参加的活动,也有可能不参加。首先使用LDA提取得到的活动内容主题数为2,则上述两个活动可以改写为T1:“British Shakespeare”、T2:“drama classic”,明显发现活动a1有50%“成员”在T1,T2这两个主题中,而活动a2有100%“成员”在主题T1,有0%“成员”在主题T2。每个活动用一个向量来表示它们的主题成员 [48],可以表示为a1 = [0.5, 0.5],a2 = [1.0, 0.0],接着用Jensen-Shannon距离来计算这两个活动的内容相似度,可以计算两个活动的内容相似度为0.31,最后利用JS divergence得到活动a1与活动a2的内容相似度为1 − 0.31 = 0.69。
2) 时空信息
时空信息指的是举办活动的时间和地理位置信息。比如上班族会倾向于周末的活动,而老年人则会对工作日的活动比较感兴趣。此外,用户对活动举办地点也有一定的青睐性,如果在时间比较短的时间内(10个小时左右)参加活动,他们会选择距离相对来说比较靠近居住地的活动;如果时间稍微长(3~5天)的时间参加活动,他们有可能会选择距离比较远的活动(如郊区的一些活动等)。此外,Liu等人 [2]也认为时空信息对活动的参与者有一定的影响 [2],因此时空信息也是影响预测问题的主要因素。对用户和活动的时空信息进行分析,有助于活动潜在参与者的预测 [49]。
3) 社交关系
用户与用户之间的社交关系也是影响预测问题的关键因素 [50][73]。比如豆瓣的活动,组织者可以给用户发活动的邀请,如果用户u1 (好友关系如图3(a)所示)被邀请,并且去参加活动,则u1会希望他的好友u2,u3,u4也会来参加。另外,如果一个用户经常去参加体育活动,该用户参加过的体育活动都是同一个组织者组织的,则该用户希望下次参加的体育活动也是之前的组织者组织。因此,社交关系也是影响预测问题的关键因素。
3.2.3. 基于亲密度最大化的方法
亲密度最大化指的是用户与用户的亲密度或者是用户与活动的亲密度最大,目前,最大化亲密度来预测活动的潜在参与者或者预测用户参加的活动已经有了部分研究。这类方法没有考虑用户居住地与活动之间的时空信息,对预测问题存在一定的局限性。
Shen等人 [51]给出的是同一个活动中考虑用户与用户之间的好友关系最大。好友之间有些是互相认识的,有些也许不认识,但是他们会因为各自朋友彼此的关系有可能即将互相成为好友关系。如图4所示,实线表示已经存在的好友关系,虚线表示潜在的好友关系。图4中(a)是已知图,若想要用从图4(a)中找到一个最大的潜在的好友亲密度去参加线下组织的活动,图4(b)中是最大的潜在好友关系,但是这些好友之间并没有互相认识的朋友,即使他们都同时到了活动举办地点,互相见面,彼此也很难相互认识。图4(c)中u2和u3有可能会形成好友,但他们之间的亲密度太小了,他们在一起参加的活动互相认识的概率也会比较小。图4(d)相对于图4(b)和图4(c)则是比较好的可以互相认识的亲密度较大的朋友关系,他们也有比较大的可能性会去参加同一个活动。若要找到亲密度最大的潜在好友圈,这是一个组合优化的问题,当用户数量增加时,可以穷举出有无数种可能性,最后变得不可计算,由此可知这是一个NP-hard问题。Shen等人仅仅考虑了用户与用户之间的好友关系,并没有考虑用户与活动的相似度和用户到活动的距离等信息,所以此方法存在较大的局限性。
针对Shen等人好友亲密度最大的局限,Li等人 [1]除了考虑在一个活动中用户与用户之间的好友关系,也考虑用户与活动之间的亲密度。Li等人认为一个用户参加某个活动,这两项亲密度是首要考虑的。例如图3(b)所示,有四个用户分别为u1,u2,u3,u4,图上顶点旁边的字母代表的是活动,有三个活动a,
b,c,这三个活动的下限分别为2,1,2;上限分别为4,6,5。从图上可知u1对活动a,b感兴趣,u2对活动a感兴趣,u3对活动b,c感兴趣,u4对活动a,c感兴趣。首先假设u1去参加活动a,从图3的(b)中好友关系可以获知u1有三个朋友,其中有两个朋友对活动a也感兴趣,而活动a的下限为2,上限为4,基于用户与活动的兴趣程度和在同一个活动中用户与用户之间的亲密度最大,因此,预测u1,u2,u3会同时去参加活动a。而目前还有u3没有参加活动,它对活动b,c都感兴趣,但是活动b只需要一个人就可以举办,而活动c则需要2个用户才可以举行,因此在符合约束条件的前提下,并且考虑了用户与活动的亲密度的情况,预测u3会去参加活动b。预测用户会参加什么活动这个问题,因为用户有多种选择,想要找到一个最优的选择是比较困难的,如果用户数目很小,可以通过穷举来预测令用户满意度较高的活动。但是在现实生活中,用户是上万个,甚至上百万的数量级,穷举法或者其他的方法在多项式时间内是不可能得到一个解。由此可知这个问题是一个NP-hard问题。鉴于此问题加了活动上下限容量的限制,把此问题变得不可解,Li等人认为在一个多项式时间内找不到常数近似比,但他们找到的近似比不超过(
)。此研究团队针对这个问题提出了静态贪心和动态贪心的求解方法,并且求得算法的时间复杂度为
,空间复杂度为
,其中L是用来执行斐波那契堆(Fibonacci head)的优先队列,E是图上边的条数。
3.3. 预测问题的方法总结
前面阐述了基于事件的社交网络数据管理预测问题的研究工作,不同的预测方法考虑的条件也各不相同,预测的内容也有所不同,现在进行总结和对比。
3.3.1. 基于组织者影响最大化的方法
这种预测方法是通过对组织者的影响力预测活动的潜在用户,利用数学方法对组织者的影响力进行抽象表示,具有一定的严谨性,可以描述预测活动潜在参与者的信息。但是这个方法仅仅考虑了活动组织者对用户的影响,而忽略了用户对活动还有偏好,比如时间和空间上的偏好,因此这种预测方法存在一定的局限性。
3.3.2. 基于多特征混合的方法
基于多特征混合方法的预测是基于影响因素的分析构建并选择特征,因此考虑了众多影响活动参与者的因素,如活动内容、时空信息以及用户的社交关系。这种方法关键在于解释各个特征对活动潜在参与者因素的相关性,该类方法不仅能预测活动的潜在用户,也能从社交关系预测用户参加的活动。
3.3.3. 基于亲密度最大化的方法
基于亲密度最大化的预测方法仅仅考虑了用户与用户之间的亲密度和用户对活动的偏好程度,忽略了用户到活动的距离这个关键因素,因此这类方法虽能预测用户参加的活动,但是预测活动的潜在用户则不太理想。因为有研究者表明,用户参加活动大部分取决于用户居住地到召集活动地点的距离 [2]。
4. 计划或安排问题
活动计划是综合考虑用户的兴趣爱好、用户居住地到召集活动地点的距离和用户的社交好友关系等特征,给用户安排令其满意度较大的活动。本节的内容将结合线上线下的社交关系介绍基于事件的社交网络服务的活动计划或安排问题。
4.1. 活动计划或安排的问题定义
首先,给出活动计划的形式化定义。有一张社交网络图G = (U, E, W),其中U表示社交网络图上的用户的集合;E是社交网络图的边的集合;W是社交网络图上边的权重的集合,代表着人与人之间的好友关系。然后再有一些活动V,目的是要找到一个活动计划或者安排 [53],使得用户满意度最大。如图5(a),圆圈里面的代表用户,三角形代表活动,图上边上的数字表示人与人之间的好友关系,图5(b)表示所有用户到所有活动的欧式距离。在没有其他限制条件的情况下,可以把u1, u2, u3安排到活动v2,把u4, u5安排到活动v1。这是图5在没有其他条件约束的情况下的一种活动安排。
4.2. 活动计划或安排的方法
活动计划或安排的目标是根据用户以及活动的属性给用户找到一个令所有用户都满意的活动计划或者路径行程。核心思想是根据用户居住地离活动召集地点的距离、用户对活动的兴趣程度和用户的社交关系 [53]来决定给用户安排什么活动或者行程路径。根据用户参加活动个数,活动计划或安排的方法包括基于亲密度最大的方法、基于最优策略的方法、基于最大–最小的方法和基于活动冲突的方法。
4.2.1. 基于亲密度最大化的方法
亲密度指的是用户与用户之间的好友关系和用户与活动的相似度,这种方法的目的是找到一个用户最感兴趣的活动,并且一个活动里面用户与用户之间的友好关系最大。Shuai等人 [12]给出用户与用户的亲密度以及用户对活动的兴趣程度,目的是找到一些列的用户去参加一个活动,使得活动里面的用户亲密度最大。如图6,图上的圆圈代表用户,圆圈里面的数字是用户对活动的兴趣程度,边的数字代表用户与用户之间的好友关系。有一个活动,假设它的容量为3,目的是从这4个人中选出3个人去参加活动,使得他们的满意度最大。如果是贪心算法,首先会安排u1去参加活动,接着安排u1的朋友u2一起去参加活动,此时亲密度为2.1。但是目前的人数还没达到活动的容量,因此再选一个用户去参加活动,根据贪心算法,会选择u3可以得到当前最大的亲密度,此时的亲密度为2.7。但是在这个例子中,如果选{u2, u3, u4},则得到的亲密度为3.0,由此可知贪心算法并不能很好的解决这个问题。于是Shuai等人提出了随机算法(CBAS) [54],假设首先基于用户与用户之间的关系和用户对活动的兴趣度之和最大选两个用户,例如图6:
;
。接着随机增加这两个用户的好友,以此来扩大活动的用户数,最后选出一个亲密度之和最大的安排,目前在这个例子中,认为安排u4一起去参加活动是比较适合。因此,此时基于亲密度最大安排的用户为{u2, u3, u4},这个安排的用户满意度为3.0,比用贪心算法的效果好 [55]。Shuai等人在随机算法的基础上加以改进(CBAS-ND),改进的方法是在随机算法的第二步以一定的概率去选择用户的朋友参加活动,并在所有条件相同的条件下,近似比会比随机贪心好。

Figure 5. The example of activity planning
图5. 活动计划的例子
此外,Li等人 [1]也提出基于亲密度之和最大的方法来给用户安排活动,但活动有上下限的要求,即如果参加活动的人数达不到活动要求下限的人数,则认为该活动无法举行;如果报名参加活动的人数已达到活动的上限人数,则认为该活动就不能再接纳其他用户的报名。先前也有研究者针对匹配问题设置了容量的限制 [56],而活动的计划或安排本质上也是一个匹配问题。Li等人在活动计划或安排上是基于亲密度之和最大的方法,该方法的基本思想是:在活动人数约束的条件下,找到一个活动安排,使得在同一个活动中,用户与用户之间的好友关系与用户对活动的兴趣程度线性之和最大。
如图6,假设有4个用户u1,u2,u3,u4,两个活动v1,v2,其中活动v1的上限为1,下限为2;活动v2的上限也为1,下限为3。圆圈的数字是用户对活动v1的兴趣程度,用户对活动v2的兴趣程度分别为0.3,0.5,0.3,0.8,Li等人给出了一种既简单又直观的方法,贪心算法。首先,计算每一对<用户,活动>的亲密度,接着选一对<用户,活动>亲密度最大的,其次检索未被安排的用户,再接着计算亲密度,最后找到一个匹配,使得所有用户到活动的兴趣和好友与好友之间的亲密度线性之和最大,则在图6的例子中最后得出的活动计划为 <1, 1>,<2, 1>,<3, 2>,<4, 2>,尖括号第一个数字表示用户,第二个数字表示活动。活动的计划或安排问题是组合优化问题,Li等人针对此问题给出相对应的理论证明 [57],当用户量达到一定的数目时,在多项式时间内找不到一个解,此外该研究团队还认为此问题在线性时间内没有常数近似比。
4.2.2. 基于最优策略的方法
最优策略指的是用户想去参加活动时,每次都会选择使自己满意度最大的策略。Armenazoglou等人 [14]基于博弈论 [58]的方法给出了活动安排的最优策略,考虑了用户到活动的欧式距离以及用户和用户之间的好友关系,但是Armenazoglou等人给出的定义中考虑的是在不同的活动中用户和用户之间的关系与用户到活动的距离线性之和最小,即目标函数为:
(6)
其中,A是活动,Au表示用户u参加的活动,d(u,Au)表示用户u到他所参加的活动的距离,wu,v表示用户u和用户v分别参加不同的活动的友好关系,α是权衡式(6)的第一项和第二项的系数。该方法的主要思想是:用户在式(6)的两项中对自己的策略进行权衡,这个算法最后终止是算法收敛至纳什均衡,即所有用户都不愿意改变自己的策略。基于这个想法,回到图5(a)中的例子,这个例子有5个用户u1,u2,u3,u4,u5,2个活动v1,v2,图5(b)中的例子是用户到活动的欧式距离,在这种情况下,找到一个最佳的活动安排使得所有用户的满意度最大。首先,把所有用户随机分配到活动中,即用户u1,u2,u3分配到活动v1,把用户u4,u5分配到活动v2,则最后每个用户的策略为u1(0.450, 0.275),u2(0.355, 0.400),u3(0.400, 0.425),u4( 0.400, 0.300),u5(0.050, 0.575),括号的第一个数字代表用户去的第一个活动的满意度,第二个数字代表用户去的第二个活动的满意度,如用户u1去活动v1的满意度为0.450,去活动v2的满意度为0.275,因此活动v2为用户u1的最佳策略,下划线为用户的最优策略。Armenazoglou等人在这个问题上用博弈论来求解,并给出了理论的结果值:最好的纳什均衡与原问题最优解的比(PoS)和最坏的纳什均衡与原问题的最差情况的解的比(PoA),其中PoS = 2;
(7)
(8)
(9)
其中degavg是度的平均数,we是边的权重。该算法的时间复杂度为
,其中k表示用户初始选择的策略数。
4.2.3. 基于最大–最小的方法
基于最大–最小的方法综合考虑了影响活动计划的三个因素,用户到活动的距离、用户对活动的兴趣程度和用户的社交关系 [59]。考虑这三个因素理由如下,例如用户a同时对活动p1,p2感兴趣,并且这两个活动都有用户a的朋友参加,其中活动p1举办的时间段为某天周六上午8:30~10:30,活动p2举办的时间段为同一天周六上午11:00~下午1:00,而从活动p1的举办地点到活动p2的举办地点需要一个小时的车程,在这种情况下,如何找到一个使得用户较满意的安排?Tong等人 [60]针对这个情景给出了最大–最小的方法,即通过分析人类参加活动的社交行为 [61],认为给用户安排活动的决定两项因素时:用户对活动的兴趣度最大,但用户到活动的距离最小,优化目标为:
(10)
(11)
其中,MaxD是任何一个用户到任何一个活动的理论最大距离,σ(u,a)是用户对活动的兴趣程度,
是一个极小的任意正数。Tong等人基于最大–最小方法给出一个有效的活动计划或安排,其本质是混合了空间信息等因素的匹配问题 [65],Tong等人针对此问题给出了启发式的方法,即Max-minBaseline (MB)、贪心(Max-minGreedy, MG)、随机贪心(Max-minRondomGreedy, MRG)和局部搜索四个算法,其中前三个算法的时间复杂度分别为
、
、
。因为这几个算法都没有近似比,则通过它们的时间复杂度比较,发现 Max-minBaseline (MB)与随机算法一样好,而贪心比这两个算法都略差。启发式算法的基本思想是:首先随机选择一个用户;接着综合考虑用户对活动的兴趣程度、用户到活动的距离,并且由于场地的规模问题,活动应该有容量限制 [62];然后基于最大–最小方法给该用户安排活动;其次看已经被安排了活动的用户的好友,如果该用户有好友,并且活动还没达到活动容量的情况下,就可以给该用户的好友安排活动,直到所有的用户被安排或者没有有效的活动为止。假设在图5中,各个用户对各个活动的兴趣程度如表1所示,其中活动括号的数字是表示活动的容量。首先,安排u2去活动v1,接着安排u5也去参加活动v1,然后u1,u3因为离活动v2比较近,而且这两个用户的友好关系也比其他用户的友好关系更亲密一些(0.4),因此安排u1,u3去活动v2,u4综合考虑三方面的因素及活动所能容纳的人数,最后给u4安排活动v2。
4.2.4. 基于活动冲突的方法
基于活动冲突的方法是考虑一个用户参加多个活动时,这些活动有时间上的冲突情况。假设用户a

Table 1. The Similarity of users and events
表1. 用户与活动的相似度
同时对活动p1,p2感兴趣,其中活动p1举办的时间段为某天周六上午8:30~10:30,活动p2举办的时间段为同一天周六上午10:00~12:00,在这种情况下,只能给用户a安排一个活动,在这种情况下,该给用户a安排哪个活动?She等人 [16][19]针对此类情况给出了活动冲突的解决办法,设置一个冲突的选项,当给用户安排活动的时候,会考虑冲突的选项。例如表2,有5个用户u1,u2,u3,u4,u5,3个活动v1,v2,v3,用户旁边括号的数字表示用户可以参加的活动个数,活动旁边括号的数字表示活动的容量,表2的数字是安排用户去参加活动的“接受能力”,表格最后一列表示活动的冲突信息,表格中的黑体表示在考虑活动无冲突的情况下,给用户安排的活动,给用户u1安排了活动v1,给用户u4安排活动v2,v3。She等人针对这个问题使用了最小成本流算法(MinCostFlow) [63]和贪心算法来求解,这两个都给出了相应的近似比,则前一个算法的近似比为1/(maxcu),后一个算法的近似比为1/(1 + maxcu),其中cu是用户可以参加的最大活动个数,比如在表2的例子中,maxcu = 3。若单纯从近似比来比较这两个算法的优劣,则贪心算法比最小成本流算法要好。
此外,She等人从上述的静态场景扩展到了动态场景,即用户是一个一个抵达,She等人针对动态场景提出了贪心算法,即每来一个用户,基于当前的情况考虑令其满意度最大的活动,一旦被安排,就不能再撤销。该研究团队针对贪心算法在动态场景也给出了理论证明,并且算法的时间复杂度为
,近似比为:
(12)
其中,wmin是用户对活动最小的满意度,在表2的例子中,wmin是0.19,V是活动的集合。同时,She等人 [13]考虑给用户安排多个无冲突活动时,结合了用户的时间和费用开销情况 [13],给用户规划行程路径。
4.3. 活动计划或安排的方法总结
活动的计划或安排是随着用户增多,会产生爆炸性组合优化的问题,当用户达到千万的数量级时,是很难在多项式时间内给出一个解。因此,活动的计划或安排是一个NP-hard难问题。大部分研究者都给出了近似算法,并且给出相应的理论证明,但是每个问题的约束条件不一样,每个问题对应的假设条件也有所不同,因此很难说哪个算法比哪个算法更优。下面对上述中的几种方法进行总结和比较。
4.3.1. 基于亲密度最大的方法
这类问题仅考虑了用户对活动的兴趣程度和在一个活动中用户与用户之间的好友关系,没有考虑用户到活动的距离。在距离方面的欠缺考虑,可能会导致用户被安排到离用户居住地很远的活动,因此这会使得用户的满意度降低。
4.3.2. 基于最优策略的方法
这类方法是基于博弈论的方法,将每个用户看成一个参与者,在每次做出选择时,都会选一个使自己满意度最大的策略。此类方法用在活动没有容量的情况下,用户可以达到最好的纳什均衡;而这类方
法没有在活动有容量限制的情况下进行讨论。
4.3.3. 基于最大–最小的方法
这类方法是考虑用户对活动的兴趣程度最大,但是用户到活动的距离最小。此类方法用了启发式的方法来解决,在很多情况下,给用户安排的活动可能并不是用户满意度最大的活动,可能会导致用户体验效果欠佳。
4.3.4. 基于活动冲突的方法
这类方法跟其他方法最大的区别是给用户安排多个活动时,考虑了一个用户同时几个活动,而活动与活动存在时间冲突的情况。一般来说,会给出一个冲突的信息,当两个活动存在冲突时,就选择一个令用户满意度较大的计划。同时,此类方法稍微增加了一些约束,比如用户的花费开销,从家到活动的距离,活动到活动的距离等信息,就可以给用户安排行程路径。
5. 推荐问题
基于事件的社交网络的推荐方法与传统的推荐方法 [11][17][30][67][68][69][88][89]有所不同,传统的推荐方法是根据个人的兴趣爱好、历史浏览、专家推荐和历史购买记录等信息来决定给用户推荐的商品 [52][66][70];而基于事件的社交网络的推荐是根据线上的用户标签信息给用户推荐群组、给群组推荐标签和给用户推荐线下活动等信息服务。因此,一些研究者以线上线下多个实体(用户、活动等)为中心,从实体的多种特征对活动进行推荐,本节将对这类工作的研究情况展开论述。
5.1. 推荐问题的影响因素
首先,对推荐问题进行形式化定义。假设基于事件的社交网络推荐问题用五元组表示
,其中
是用户的集合,对于每一个用户u
i,利用
表示它的地理位置信息,并且每个用户都有对应的标签信息,
表示用户与用户好友关系的集合;
是活动的集合,对于每一个活动v
j Î V,利用
表示它的地理位置信息;
表示标签的集合,
表示群组的集合,每一个群组都有一个相应的地理位置信息和一个标签信息。有三种推荐模式:① 给用户推荐群组,给定一个用户u,根据r(u,g)的排序给该用户推荐一个其偏好程度最大的群组,其中r(u,g)表示用户u对群组g的偏好 [11];② 给群组推荐标签,已知一些历史的群组标签对
,给定一个目标群组,目的是找到一些列的标签使得它们与目标群组有较大的相似度 [71];③ 给用户推荐活动,给定一些用户,根据r(u,v)给用户推荐其感兴趣的并即将到来的活动 [2]。无论是哪种推荐结果,都是由多种因素共同作用,这使得看似简单的问题变得具有挑战。针对不同的推荐结果,考虑的因素将有所不同。本文综合以往研究内容,将影响推荐的因素概括为三类——时空因素、内容因素和社交关系。时空因素主要包括举办活动的地理位置信息和时间信息 [5];内容因素主要包括活动自身的特点以及活动内容与用户的兴趣爱好相吻合的程度;社交关系主要包括组织者的影响力以及用户与用户组成的群组 [53]。
5.2. 推荐问题的方法
推荐是指学习过往的历史记录和行为规律,从而给未来的群组、标签和活动推荐用户、群组等。根据推荐基本假设的不同,推荐方法可分为基于用户历史记录的推荐、基于多任务的推荐和基于多特征的推荐。主要使用的模型:贝叶斯潜在因子模型 [72]、聚类模型 [2]、概率模型 [18]、矩阵分解 [11][73]、分类模型 [3]、排序算法 [3]和基于图的模型 [17]等。
5.2.1. 基于用户历史记录的推荐方法
基于用户历史记录的推荐方法依据用户在推荐时间点前的历史纪录信息,根据用户参加过的活动、标签信息、地理位置记录等给用户推荐活动。历史纪录信息对用户未来参加的活动有着很好的指导作用,例如发现用户以往总是参加一些体育类的活动,则社交媒体平台会以很大的概率给他推荐体育类相关的活动。Qiao等人 [18]对Meetup的反馈数据(“RSVP”选择,“yes”,“no”,“maybe”)进行统计分析,发现用户会跟自己住的地点与召集活动的地点有很大的关系,然后根据用户的兴趣爱好使用贝叶斯概率模型 [78],为用户推荐其可能会参加的活动。Liu等人 [2]对Meetup的反馈数据进行聚类分析,发现用户大多选择离居住地较近的活动,因此可以认为距离是可以用来推荐的一个关键因素。
Zhang等人 [11]依据用户反馈数据、用户对活动的兴趣程度和时空信息进行建模,接着采用矩阵分解技术给用户推荐群组 [75][76],其核心思想是:假设给用户推荐群组只受少数几个因素的影响,由此将稀疏高维的“用户–群组”的矩阵分解为两个低维矩阵,通过挖掘用户对群组的偏好程度得出用户特征矩阵Pu和群组特征矩阵Pg,然后依据
重构用户对群组喜好的低维矩阵 [77],同样地,依据
用来构建用户对群组的偏好矩阵,最后依据
得出用户对群组的兴趣程度的矩阵 [74]。然而由于新的用户和新的活动不断出现,用户-活动矩阵将会变得非常稀疏,则会存在较严重的冷启动问题。因此,在后续的研究工作 [3]致力于分析用户历史记录的基础上融入更丰富的特征,如用户属性特征、活动属性特征、活动召集的时空信息和用户参加活动的时间段等。其中,文献 [3]是基于多特征的推荐方法,在一定程度上缓解了数据稀疏导致的冷启动问题。
5.2.2. 基于多任务的推荐方法
多任务推荐指的是给用户推荐群组、给群组推荐标签和给用户推荐活动,Pham等人 [17]假设基于事件的社交网络是由用户、标签、群组、活动、活动举办地点这五个实体构成,并对这五个实体进行建模,与其他的建模方法 [78]不同的是,它主要解决了给用户推荐群组、给群组推荐标签和给用户推荐活动。用
表示五个实体的关系,而基于事件的社交网络由有向图
组成,其中
组成,
,并且m与n具有关系},例如在图7中,R是users,events,tags,groups,venues;
是它们之间的关系。
如图7,Alice和Bob一起加入“Sports club”群组,然而Carol加入“Singles”群组;“Sports club”群组在体育场举行足球比赛,意味着Alice和Bob将会去体育场参加足球比赛;以此同时,“Singles”群组在“Restaurant”举办“Birthday”和“Hanging out”两个活动,则意味着Carol将有可能去“Restaurant”参加那两个活动。此外,发现前两个人的标签为“Sports”而后一个人的标签为“Dancing”,两个群组都是用“Games”来作为标签表示群组的兴趣爱好,“Singles”群组还用“Dancing”来作为标签。在这么交错复杂的信息中,将产生三个问题。① 用户将加入哪个群组,比较方便其往后参加的活动与兴趣爱好相吻合?② 群组将会选择哪个标签才是最能表达它的信息?③ 把即将到来的活动推荐给哪个用户比较适合?Pham等人 [17]针对这三种推荐任务给出了基于图的模型方法(HeteRS),将这三种推荐任务转变

Figure 7. The example of recommendation [17]
图7. 多种推荐任务示例图 [17]
为顶点近似计算问题(node proximity calculation problem) [79],并结合异质的网络信息,接着采用马尔科夫链去解决这三种推荐问题。
5.2.3. 基于多特征的推荐方法
基于多特征是依据多个特征给用户推荐活动或给用户推荐群组。不同于传统的群组推荐 [81][82],基于事件的社交网络的群组推荐主要是结合线下的活动,一系列的用户会在线下共同参加一个活动。Q. Macedo等人 [3]结合了活动内容,历史记录的反馈数据和用户及活动的时空信息,假设这些属性都对用户参加活动起到一定的影响 [84]。例如,一个用户决定去参加一个活动,不仅仅因为这个活动与他的兴趣爱好吻合,还考虑了该用户的朋友也会去参加这个活动。在分析多特征对推荐影响的因素时,采用了坐标上升(Coordinate Ascent)学习方法,把与用户和活动相关的属性逐步考虑到模型当中,然后设计多组对比实验,最后才能知道哪个特征是对推荐有意义。Q. Macedo等人针对多特征的模型求解中用到了分类算法和坐标上升的排序算法。此外,Tong等人 [64]也考虑了多特征的推荐方法,结合用户居住地到召集活动地点的距离、用户对活动的兴趣程度以及用户的社交关系,给用户推荐活动或者行程路径。
5.3. 推荐问题的方法总结
现在总结上文介绍的基于用户历史记录的推荐、基于多任务的推荐和基于多特征的推荐,这三种推荐方法都有其各自的特点,现对其进行总结。
5.3.1. 基于用户历史记录的推荐方法
这种推荐方法要事先知道用户的历史记录,并且从历史记录统计分析出少部分关键的特征,这类方法主要利用了矩阵分解技术来求解,主要是挖掘用户的历史记录信息,分析出用户的兴趣偏好,这些信息给推荐具有一定的指导作用。随着新用户和新活动的进入,此类方法将面临严重的冷启动问题,若融入多个特征属性,则冷启动问题将得到缓解。基于用户历史记录的推荐方法可以利用在给用户推荐群组,给用户推荐活动这两个推荐任务上面。
5.3.2. 基于多任务的推荐方法
这种推荐方法结合用户和活动的五个属性,解决了给用户推荐群组,给群组推荐标签和给用户推荐活动三种推荐任务,这类方法主要利用了基于图的模型的方法,把这三种推荐任务转变为顶点近似计算问题(node proximity calculation problem),并结合异质的网络信息。而对于信息量较少的用户和活动,则这种方法将很难给用户推荐其感兴趣较大的活动,很难给群组推荐适合的标签,可能会给用户推荐其不太满意的活动,影响用户的满意度。但是这种方法能解决三种推荐任务也是其他研究者少有的突破。
5.3.3. 基于多特征的推荐方法
这种推荐方法是为了解决基于用户历史记录的推荐方法所带来的冷启动问题,主要用到了分类方法和坐标上升的排序算法来解决。这种方法主要难点是在特征的选择,将选择好的特征用分类算法去分类,这种方法比较直观、简单。但是模型适应性和解释性较弱,依赖于特征的选择和组合。
6. 总结与展望
基于事件的社交网络既能满足社会化活动推荐的基本功能,同时又具备给用户指定活动计划或者路线规划并且预测活动的潜在用户等特点。近年来,基于事件的社交网络的研究和应用取得了一定的进展,但总体来看还是有一些方向值得关注。这一节先对本文进行总结,接着对基于事件的社交网络的研究趋势进行分析。
6.1. 总结
在基于事件的社交网络中,用户会根据社交媒体平台的信息随时随地获知线下的活动,近年来,社交媒体平台的注册人数逐年上升,因此基于事件的社交网络数据管理技术在学术界和工业界受到了越来越多的关注。本文从预测、活动计划或安排以及推荐对基于事件的社交网络数据管理技术进行了综述,首先从研究的模型把预测问题分为基于组织者影响最大、基于多特征混合和基于亲密度最大的方法:然后依据用户参加的活动个数,对计划或安排问题分为亲密度最大、最优策略、最大–最小和活动冲突的方法;接着从用户历史记录、多任务的推荐方法和多特征的推荐方法来介绍推荐问题。本文使用一个表格总结如表3。
在表3中,CBAS-ND与CBAS是可比较的,因为这两个算法是在同一个问题规模并且约束条件相同的情况下进行的,从上文的介绍中,可以知道CBAS-ND比CBAS的算法性能好,记CBAS-ND算法的时间复杂度为
。在表3中的路径规划三个算法,它们的约束条件和限制条件都一致,因此他们也是可比较的,但是从文章中可以知道RG算法是没有近似比的,记RG的时间复杂度为
,算法在没有近似比的情况下,无从得知该算法的好坏;而DeDP和DeGreedy它们都有1/2的近似比,从时间复杂度来看的话,DeGreedy算法优于DeDp算法,记DeDP的时间复杂度为
,DeGreedy的时间复杂度为

Table 3. Summarized of activity arrangement
表3. 基于事件的社交网络总结表
。在表3中的算法时间复杂度,其中
表示用户数,
表示事件数,m是刚开始随机的选择的用户的个数,
表示用户可以参加的事件个数,
表示事件可以容纳的用户数量,
是用户u参加事件需要的开销费用,
是事件v用户的集合。本文对MCF-GEACC算法的时间复杂度进行了简化,从原时间复杂度简化为
,并记为
;同时也对算法G-GEACC的时间复杂度进行了化简,由于
与
是大于1的数,因此原来的时间复杂度可化为
,并记为
。
6.2. 发展趋势分析
经过多年的发展,虽然研究者们已经针对预测、活动的计划或安排和推荐进行了一些相关的研究,但是依然存在很多的问题尚未涉足。从本文的论述中,笔者认为基于事件的社交网络数据管理技术有如下的发展趋势:
趋势一:提高用户的满意度
基于事件的社交网络数据管理技术,结合实际意义,一般是要考虑多条件的限制才会使得问题更真实。比如用户到活动举办地点的距离、用户与活动之间的相似度、线上用户之间的友好关系和活动的容量等,但是考虑了多个条件的限制,问题就会变得复杂渐渐地接近无解的状态,所以结合实际应用环境并针对这么多有意义地条件限制的情况下,如何在可接受的时间复杂度和空间复杂度范围内,设置一个较优的算法使得用户的满意度达到前所未有的高度。
趋势二:研究用户和活动的动态性
目前基于事件的社交网络数据管理技术大部分研究都是在用户和活动所有信息已知的情形下提出,基于事件的社交网络的静态数据模型假设过于严格,无法建模现实世界中的基于事件的社交网络数据。因为在现实生活中,由于用户和活动的变化,用户会一个接一个的动态报名参加活动,活动也会一个接一个的动态出现。而目前研究人员提出的基于事件的社交网络数据管理技术研究只有极少部分可以应用在用户与活动双方动态抵达的环境中 [85]。因此用户和活动的部分信息未知的研究还有待开发。
趋势三:真实结果与理论结果的对照
目前的很多研究都是基于一些算法给用户推荐活动或者安排活动,但是现实生活中用户有没有去参加这些活动,此研究目前还比较缺乏 [87]。这个研究方向需要研究人员花费大量的精力,首先要去国内外基于事件的社交网络数据管理的网站进行爬虫,然后找出用户真实参加的活动与用算法理论去推荐或者安排的活动进行对照,最后统计分析用户真正去参加活动的真实特征。有时候用户不一定会考虑全部信息才会去参加活动,也许用户仅仅只想着找一个举办地点离自己最近的活动。因此,用户真实参加的活动和用算法推荐或者安排用户去参加的活动,这两者存在一定的差距,如何找出这个差距是下一步研究的关键任务。

