摘要:该文研究了三种气体Euler方程在小初值的情况下解的整体存在性及大时间行为问题。本文的主要内容是定理1.1的证明。首先给出引理3.1,对于
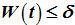
充分小,利用Hölder不等式,Young不等式等计算方法将未知函数
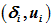
关于x的导数用
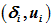
关于时间t的导数进行估计。然后用标准能量估计方法,对浓度通量
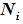
估计;最后构造
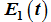
函数与
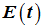
等价,证明出
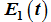
满足一致有界且指数衰减速率,从而得到
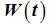
也是一致有界且指数衰减速率。
Abstract:In this paper, the global existence and large time behavior problem of three gases of Euler equation in the small initial value are studied. The main content of this chapter is the proof of theorem 1.1. First of all, we first give a lemma 3.1 for a
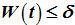
sufficiently small. Using the Hölder inequality, Young inequality and other calculation methods, the derivative of unknown function
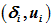
with respect to x is estimated using the derivative of
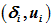
with respect to time t. Then, standard energy estimation method is used to estimate the concentration of flux
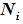
. Finally, by constructing the
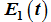
and function
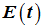
equivalent, we prove
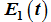
meets uniformly bounded and exponential decay rate, so as to get
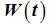
is uniformly bounded and exponential decay rate.