1. 引言
结构变阻尼半主动控制装置一般是在传统的液压流体阻尼器或黏滞阻尼器的基础上,设置可控伺服阀构成具有控制流体流量、连续改变阻尼力、控制宽频带多种激励振动能力的“智能”阻尼器。
Hrovat [1] 首先提出结构变阻尼半主动控制AVD系统,它实质上是一种节流孔的大小可以调节的粘性液体阻尼器,在每一采样周期内根据一定的控制律实时调节装置的阻尼特性,从而达到减震目的。该系统在美国、日本已有实际应用。Ruangrassamee等 [2] 提出粘滞–变摩擦阻尼算法,综合了粘滞阻尼器和摩擦阻尼器的优点。日本建成了Kajima Shizuoka变阻尼控制的建筑,并在实际小震作用下展示出了很好的控制效果 [3] 。孙作玉与李惠分别对建筑结构主动变阻尼控制进行了研究,并研制开发了主动变阻尼装置 [4] [5] 。Yanqing Liu Hiroshi Matsuhisa [6] 提出了新的半主动控制装置,由两个可变系数的阻尼器以及两个常数弹簧构成,给出了这种半主动控制装置的理论与试验分析结果。H. R. Owji,A. Hossain Nezhad Shirazi,H. Hooshmand Sarvestani [7] 讨论了设有新型半主动调频质量阻尼器SADA-TMD以及主动调频质量阻尼器ATMD的结构反应特点。谭平,周福霖 [8] 基于变刚度和变阻尼的原理提出两种用于耦联结构体系的半主动控制装置,建立了这两种半主动控制耦联结构振动控制体系的运动方程,提出一种新的广泛适用于一般开关控制型半主动控制系统的控制算法。
尽管目前已经有了一些研究成果及工程实例,但已有的论著中普遍侧重通用理论方面的介绍,或介绍装置本身的性能。对于具体的结构如何建立模型、数值算法实现以及减震性能评估仍然需要进一步的研究。本文以一栋20层结构分别设置变阻尼半主动控制装置为例,首先建立其数学模型,然后根据结构动力反应数值计算方法编写求解软件,根据计算结果分析变阻尼半主动控制装置的减震效果。
2. 运动方程建立
2.1. 结构模型
设置变阻尼半主动控制装置的结构简图如图1所示。与主动最优控制相比,它不是依靠外部的作用力,而是利用结构层间的相对位移和相对速度,使阻尼器活塞产生运动,改变阻尼器中的阻尼系数,被动地产生阻尼力。因此变阻尼器也只能部分地实现主动控制的目标。图2是结构分析模型。
2.2. 结构运动方程的建立
设置半主动控制装置的多自由度体系的运动方程为:
(1)
其中x是层间位移差;
是外力列向量;
是变阻尼半主动控制装置阻尼力列向量,其中的第i个元素代表设置在第i楼层变阻尼半主动控制装置提供的阻尼力;M是体系质量矩阵,C是体系自身阻尼矩阵,K是体系刚度矩阵,Bs是变阻尼半主动控制装置位置矩阵,M、C、K、Bs具有如下的形式:
变阻尼半主动控制装置能实现的控制力Udi(t)可以表示为 [9] :
(2)
式中
是楼层i阻尼器外套与活塞之间的速度差,
是变阻尼半主动控制装置的阻尼系数,它可以通过改变阻尼器的输入电压从而改变主动变阻尼控制装置的伺服阀的开口大小来调节;因为主动变阻尼控制装置是以阻尼力的形式提供控制力,需要被动地依赖于结构振动的速度,因此只能提供与结构运动方向相反也即阻止结构运动的控制力。主动变阻尼装置的最大阻尼力不是一个特殊的限制,故在可比条件下两者的最大出力都是有限的。通常采用简单Bang-Bang控制算法,或对其做相应的修改,成为最优Bang-Bang控制算法,确定阻尼力的大小。
1) 简单Bang-Bang变阻尼半主动控制算法可以表示为:
(3)
2) 最优Bang-Bang变阻尼半主动控制算法可以表示为:
(4)
和
分别是主动变阻尼装置在伺服阀完全打开和关闭时的阻尼系数,也即装置能提供的最小阻尼系数和最大阻尼系数。ui体系最优控制力(可以是LQR最优控制或其他类型的最优控制)
中楼层i的控制力。求最优控制力U的增益反馈矩阵
的Ricatii方程为 [9] :
求出P之后,再代入
中(
为最优控制系统的加速度反应)可求得最优控制力U。将
代入到运动方程(1)就可以求得半主动控制结构地震动力反应。可以采用的数值积分法有Newmark-β法、Runge-Kuta法等。
3. 计算实例与结果
为了具体定量地考察变阻尼半主动控制装置的减震效果,以一个20层建筑结构为例,简化成一个20个集中质量的离散多自由度系统,mi= 2933 t,ki= 28,950,000 kN/m,ci= 22,000 kN∙s/m。在各楼层设置变阻尼半主动控制装置。输入地震波为Elcentro波。最大水平地面加速度为
= 4.0 m/s2,地震烈度相当于8度。对两种减震方案在地震作用下的动力反应分析计算,得到如下结果如表1及图3~图9。
4. 计算结果分析
从表1可以看出,采用简单Bang-Bang和最优Bang-Bang控制算法对层间位移能产生很好的减震效果,当取cdmax= 280000 kN∙s/m、cdmin= 20000 kN∙s/m时,与无控制结构相比,其减震效果能达到25%~45%;对于楼层加速度而言,简单Bang-Bang中楼层加速度的减震效果沿楼层变化不均匀,故其效果不显著,而在最优Bang-Bang中效果较好。
从图4、图5中可以看出,简单Bang-Bang控制算法和最优Bang-Bang控制算法在结构地震动力反应时程上表现良好,楼层位移和楼层加速度随时间衰减很快。
从图6中可以看出,对层间位移、楼层加速度,AMD主动控制的减震效果最优,最优Bang-Bang控制算法较好于简单Bang-Bang控制算法,但均优于无控制状态;对楼层加速度来说,简单Bang-Bang和最优Bang-Bang控制算法都有一定的减震效果,最优Bang-Bang控制算法效果较简单Bang-Bang显著。
从图7及图8可以看出,cdmax越大,减震效果越好。从图9可以看出,在同一参数指标下,简单Bang-Bang控制算法所需要的控制力与最优Bang-Bang控制算法相近,但最优Bang-Bang控制力略高于简单Bang-Bang控制力。

Figure 4. Time histories of structural seismic dynamic response (simple Bang-Bang algorithm)
图4. 结构地震动力反应时程(简单Bang-Bang算法)

Figure 5. Time histories of structural seismic dynamic response (optimal Bang-Bang algorithm)
图5. 结构地震动力反应时程(最优Bang-Bang算法)
对半主动控制来说,若要达到与AMD主动控制同样的控制效果,由于Bang-Bang控制算法的特点,需要具备较大的cdmax。在一般的条件下,由半主动控制装置不易达到AMD主动控制效果,但半主动控制装置实施方便,不需要很大的外部能量。
本文考虑的情况是在每一楼层都设置变阻尼半主动减振装置,只是为了将计算结果做一个全面、通用化的对比。在实际控制方案设计时不需要每一楼层都设置控制装置。这时只需要将相应主动变阻尼器控制力撤去,使其值为0,就可以计算相应的地震动力反应,考察评价其减震效果,这里不详细介绍。
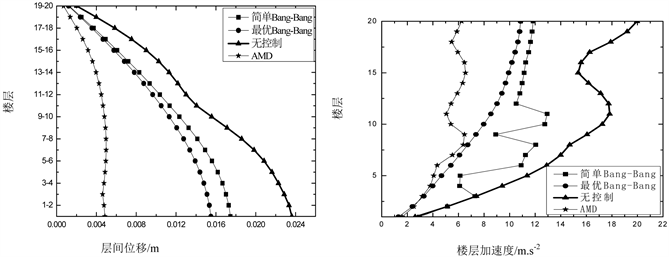
Figure 6. Structural seismic dynamic response
图6. 结构地震动力反应

Figure 7. Structural seismic dynamic response (simple Bang-Bang)
图7. 结构地震动力反应(简单Bang-Bang)
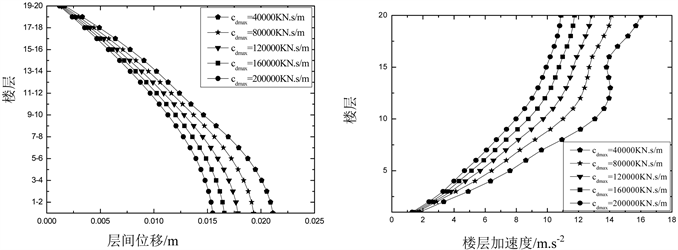
Figure 8. Structural seismic dynamic response (optimal Bang-Bang)
图8. 结构地震动力反应(最优Bang-Bang)
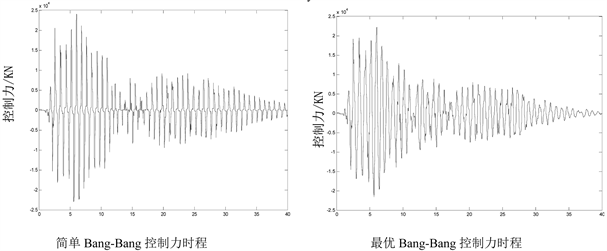
Figure 9. Time histories for semi-active control forces
图9. 半主动控制力时程

Table 1. Control mode vs seismic dynamic response
表1. 控制方式与地震动力反应
5. 结论
1) 变阻尼半主动控制对层间位移和楼层位移有较明显的减震效果,可以通过调整其参数指标cdmax达到目标减震效果,减震效率可达到25%~45%。
2) 简单Bang-Bang控制力与最优Bang-Bang基本相近,但最优Bang-Bang控制比简单Bang-Bang控制力稍大。cdmax越大,层间位移及楼层位移动力反应减震效率越高。
3) 变阻尼半主动控制装置对楼层加速度减震有一定效果。尤其是最优Bang-Bang效果比简单Bang-Bang好。
4) 本文所提供的数据和结论可以为多自由度半主动变阻尼系统在高层建筑的实验和实际应该用提供理论参考和对比。
基金项目
国家自然科学基金项目(51378170)。
NOTES
*通讯作者。