带有组织重塑的肿瘤侵袭趋同化模型在三维空间中的整体存在性

期刊菜单

带有组织重塑的肿瘤侵袭趋同化模型在三维空间中的整体存在性
Global Existence for a Haptotaxis Model of Cancer Invasion with Tissue Remodeling in Three Dimensions

DOI:10.12677/AAM.2018.79139,PDF,HTML,XML,下载: 1,098浏览: 1,540
作者:孟莱青,苑佳：北京航空航天大学，数学与系统科学学院，北京
关键词:趋同化；整体解；Gagliardo-Nirenberg不等式；Haptotaxis；Global Solution；Gagliardo-Nirenberg Inequality

摘要:在与相同的假设条件下，本文主要通过Gagliardo-Nirenberg不等式，建立趋同项在三维空间上的先验估计，给出趋同化模型在三维空间中整体解的存在唯一性。

Abstract:Compared with, under the same assumption on the coefficients, we establish some delicate priori estimates of haptotaxis term by using the Gagliardo-Nirenberg inequality, and prove the global existence and uniqueness of classical solutions to haptotaxis model in three dimensions.

文章引用：孟莱青, 苑佳. 带有组织重塑的肿瘤侵袭趋同化模型在三维空间中的整体存在性[J]. 应用数学进展, 2018, 7(9): 1197-1202. https://doi.org/10.12677/AAM.2018.79139

1. 引言

癌症侵袭是一个非常复杂的过程，涉及多种生物学机制。细胞迁移在多种生理和病理过程中起着非常重要的作用，包括胚胎发育、皮肤创伤愈合、肿瘤浸润和转移。事实上，许多数学模型已经被开发用于癌症侵袭的相关方面。其中趋同性是细胞迁移的重要机制。它是细胞沿着细胞粘附梯度的定向运动，这往往是由趋化因子或结合在细胞外基质(ECM)中的酶促进的。为此，学者们提出了更多的生物学相关模型，做了很多尝试且得到了可观的结果 [2] - [9] 。局部解的存在唯一性、整体解的存在性、解的有界性、爆破解的存在性等都是癌症侵袭模型的主要内容。文章 [1] 给出了如下模型：

${\begin{cases} u_{t} = Δ u - ξ \nabla \cdot (u \nabla ω) + μ u (1 - u - ω), x \in Ω, t > 0, \\ υ_{t} = Δ υ - υ + u, x \in Ω, t > 0, \\ ω_{t} = - υ ω + η ω (1 - ω - u), x \in Ω, t > 0. \end{cases}$ (1.1)

其中 $Ω \subset ℝ^{d} (d = 2, 3)$ 是边界光滑的有界区域。为了封闭方程组，我们需要施加边界和初始条件，如下：

${\begin{cases} - \frac{\partial u}{\partial ν} - ξ u \frac{\partial ω}{\partial ν} = \frac{\partial υ}{\partial ν} = 0, x \in \partial Ω, t > 0, \\ u (x, 0) = u_{0} (x), υ (x, 0) = υ_{0} (x), ω (x, 0) = ω_{0} (x), x \in Ω . \end{cases}$

$\frac{\partial}{\partial ν}$ 表示边界上的外法向量， $u, υ, ω$ 分别代表癌细胞密度、基质降解酶(MDE)的浓度和细胞外基质(ECM)的密度。同时， $μ$ 代表细胞增值速率， $ξ > 0$ 是衡量细胞趋同性敏感度的参数， $η > 0$ 表示ECM重塑的速率参数。

为了下文中分析的方便，我们引入下面的变量变换

$a = u e^{- ξ ω},$

得到与(1.1)等价的形式

${\begin{cases} a_{t} = e^{- ξ ω} \nabla \cdot (e^{ξ ω} \nabla a) + ξ a υ ω + a (μ - ξ η ω) (1 - e^{ξ ω} a - ω), x \in Ω, t > 0, \\ υ_{t} = Δ υ - υ + e^{ξ ω} a, x \in Ω, t > 0, \\ ω_{t} = - υ ω + η ω (1 - ω - e^{ξ ω} a), x \in Ω, t > 0, \\ \frac{\partial a}{\partial ν} = \frac{\partial υ}{\partial ν} = \frac{\partial ω}{\partial ν} = 0, x \in \partial ω, t > 0, \\ a (x, 0) = a_{0} (x), υ (x, 0) = υ_{0} (x), ω (x, 0) = ω_{0} (x), x \in Ω . \end{cases}$ (1.2)

在文章中，我们假设

${\begin{cases} a_{0} (x) \geq 0, υ_{0} \geq 0, 0 \leq ω_{0} \leq 1, \\ \partial Ω \in C^{2 + α}, 0 < α < 1, \\ a_{0} (x), υ_{0} (x), ω_{0} (x) \in C^{2 + α} (\bar{Ω}), \\ \frac{\partial a_{0} (x)}{\partial ν} = \frac{\partial υ_{0} (x)}{\partial ν} = 0, x \in \partial Ω . \end{cases}$ (1.3)

2. 预备知识

对任意 $0 < T < \infty$ ，设

$Q_{T} = Ω \times {0 < t < T}, Γ_{T} = \partial Ω \times {0 < t < T} .$

给出以下空间及模的相关定义：

$W_{p}^{2} (Ω) = {u | u, D_{x} u, D_{x}^{2} u \in L^{p} (Ω)},$

$W_{p}^{2, 1} (Q_{T}) = {u | u, D_{x} u, D_{x}^{2} u, D_{t} u \in L^{p} (Ω)}$

和

${‖ u ‖}_{W_{p}^{2} (Ω)} = {‖ u ‖}_{L^{p} (Ω)} + {‖ D_{x} u ‖}_{L^{p} (Ω)} + {‖ D_{x}^{2} u ‖}_{L^{p} (Ω)},$

${‖ u ‖}_{W_{p}^{2, 1} (Q_{T})} = {‖ u ‖}_{L^{p} (Q_{T})} + {‖ D_{x} u ‖}_{L^{p} (Q_{T})} + {‖ D_{x}^{2} u ‖}_{L^{p} (Q_{T})} + {‖ D_{t} u ‖}_{L^{p} (Q_{T})} .$

其中 $p \geq 1$ 是一个整数。

为了表述方便，在文章中， $c_{i} (i = 1, 2, \dots)$ 和C均代表不依赖于时间的正常数， $A_{i} (i = 1, 2)$ 是依赖于最大生命区间T的常数。

引理2.1：设 $Ω \subset ℝ^{n}$ 是带有光滑边界的有界区域。取 $l, k$ 是任意整数，满足 $0 \leq l < k$ ，令 $1 \leq q, r \leq \infty$ ， $p \in ℝ^{+}, \frac{l}{k} \leq θ \leq 1$ 满足

$\frac{1}{p} - \frac{l}{n} = θ (\frac{1}{q} - \frac{k}{n}) + (1 - θ) \frac{1}{r} .$

那么，对于任意 $u \in W^{k, q} (Ω) \cap L^{r} (Ω)$ ，存在两个依赖于 $Ω, q, k, r, n$ 的正常数 $c_{1}$ 和 $c_{2}$ 使得以下不等式成立：

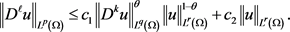
如果 $1 < q < \infty$ ， $k - l - \frac{n}{q}$ 是非负整数，那么对 $\frac{l}{k} \leq θ < 1, r > 1$ ，上述不等式亦成立。

3. 本文的主要内容

本节我们分三部分介绍。

3.1. 局部存在性与唯一性

定理3.1：(局部存在性与唯一性)在初始条件(1.3)的条件下，若取某个小值 $T_{0} > 0$ ，则对任意 $p > 5$ ，系统(1.2)存在唯一的强解 $(a, υ, ω) \in {(C^{2 + l, 1 + \frac{l}{2}} (\bar{Q_{T_{0}}}))}^{3}$ 成立。而且

$a \geq 0, υ \geq 0, 0 \leq ω \leq 1.$

证明：通过调用已建立的Banach不动点定理以及应用标准抛物线正则性理论(参见 [10] )，可以很容易地验证经典解的局部存在性、唯一性和可扩展性准则(参见参考文献 [1] [2] [3] )。同时，在最大值原理的帮助下，我们也可以验证解的非负性。

3.2. 在二维和三维空间中的L^∞先验估计

引理3.1：假设 $(a, υ, ω) \in {(C^{2, 1} (Q_{T}))}^{3} (T > T_{0})$ 是系统(1.2)的解，那么，对所有时间 $t \in (0, T)$ ，成立

${‖ a (t) ‖}_{L^{1} (Ω)} \leq u {(t)}_{L^{1} (Ω)} \leq \max ({‖ u_{0} ‖}_{L^{1} (Ω)}, | Ω |),$

${‖ υ (t) ‖}_{L^{1} (Ω)} \leq {‖ υ_{0} ‖}_{L^{1} (Ω)} + \max ({‖ u_{0} ‖}_{L^{1} (Ω)}, | Ω |) .$

证明：主要利用霍尔德不等式和柯西-施瓦兹不等式，可以很容易的验证上述引理成立。

引理3.2：在初始条件(1.3)的条件下，假设 $υ_{0} \in W_{\infty}^{1} (Ω)$ ， ${‖ u ‖}_{L^{q} (Ω)} \leq C$ ，那么对所有时间 $t \in (0, T)$ ，

1) 对于 $1 \leq q < n$ ，当 $p < \frac{q n}{n - q}$ ，我们有 ${‖ υ (t) ‖}_{W_{p}^{1} (Ω)} \leq C$ ；

2) 对于 $q = n$ ，对任意 $q < \infty$ ， ${‖ υ (t) ‖}_{W_{p}^{1} (Ω)} \leq C$ 均成立；

3) 对于 $q > n$ ，当 $q = \infty$ 时， ${‖ υ (t) ‖}_{W_{p}^{1} (Ω)} \leq C$ 仍然成立；

4) 对于 $1 \leq q < \infty$ ，当 $r > q$ 且满足 $\frac{1}{r} + \frac{2}{n} > \frac{1}{q}$ 时，成立 ${‖ υ (t) ‖}_{L^{r} (Ω)} \leq C$ 。

引理3.3：假设 $(a, υ, ω) \in {(C^{2, 1} (Q_{T}))}^{3} (T > T_{0})$ 是系统(1.2)的解，且 $μ \geq ξ η$ 。那么对所有时间 $t \in (0, T)$ ，下面估计成立：

${‖ a (t) ‖}_{L^{\infty} (Ω)} \leq C, {‖ υ (t) ‖}_{W_{\infty}^{1} (Ω)} \leq C .$

详细的证明过程我们可参考文献 [1] 。

3.3. 在二维和三维空间中关于 ${‖ \nabla ω ‖}_{L^{q} (Ω)}$ 的先验估计

在二维空间中，关于 ${‖ \nabla ω ‖}_{L^{q} (Ω)}$ 的先验估计在文献 [1] 中给出了详细的证明，现在我们给出在三维空间中，关于 ${‖ \nabla ω ‖}_{L^{q} (Ω)}$ 的先验估计。两者的区别在于估计 $\int_{0}^{T} {‖ Δ a (t) ‖}_{L^{2} (Ω)}^{2} d t$ 的证明过程不同。

引理3.4：假设 $(a, υ, ω) \in {(C^{2, 1} (Q_{T}))}^{3} (T > T_{0})$ 是系统(1.2)的解，那么对所有时间 $t \in (0, T)$ ，成立

${‖ \nabla ω (t) ‖}_{L^{p} (Ω)}^{p} \leq e^{c_{3} t} [c_{4} + c_{5} \int_{0}^{t} {‖ \nabla a (s) ‖}_{L^{p} (Ω)}^{p} d s];$

${‖ \nabla a (t) ‖}_{L^{2} (Ω)} \leq c_{6} e^{ξ η t} .$

${‖ a_{t} ‖}_{L^{2} (Q_{T})} \leq C t + C e^{ξ η t} .$

详细的证明过程我们可参考文献 [1] [2] 。

引理3.5：假设 $(a, υ, ω) \in {(C^{2, 1} (Q_{T}))}^{3} (T > T_{0})$ 是系统(1.2)的解，在三维空间中有

$\int_{0}^{T} {‖ Δ a (t) ‖}_{L^{2} (Ω)}^{2} d t \leq C (t) .$

证明：因为 $a_{t} = Δ a + ξ \nabla ω \cdot \nabla a + h (x, t)$ ，其中

$h (x, t) = ξ a υ ω + a (μ - ξ η ω) (1 - ω - e^{ξ ω} a) .$

因为引理3.3，得到 $h (x, t)$ 满足

$\begin{matrix} {‖ h (x, t) ‖}_{L^{\infty} (Ω)} = {‖ ξ a υ ω + a (μ - ξ η ω) (1 - ω - e^{ξ ω} a) ‖}_{L^{\infty} (Ω)} \\ \leq ξ {‖ a ‖}_{L^{\infty} (Ω)} {‖ υ ‖}_{L^{\infty} (Ω)} + μ {‖ a ‖}_{L^{\infty} (Ω)} \leq c_{7} . \end{matrix}$

结合引理3.4，我们得到对任意 $0 < t \leq T$ ，

$\int_{0}^{t} {‖ Δ a ‖}_{L^{2} (Ω)}^{2} d s \leq c_{8} T + c_{9} e^{2 ξ η T} + 2 ξ^{2} \int_{0}^{t} {‖ \nabla ω \cdot \nabla a ‖}_{L^{2} (Ω)}^{2} d s .$ (3.1)

我们需要进一步估计上式右边最后一项，该项来源于趋同化项。利用霍尔德不等式、引理3.4、柯西不等式以及对任意 $x, y \geq 0$ 成立 ${(x + y)}^{\frac{1}{2}} \leq x^{\frac{1}{2}} + y^{\frac{1}{2}}$ ，我们得到对任意 $0 < t \leq T$ ，

$\int_{0}^{t} {‖ \nabla ω \cdot \nabla a ‖}_{L^{2} (Ω)}^{2} d s \leq \sqrt{t} c_{10} e^{c_{11} T} \int_{0}^{t} {‖ \nabla a ‖}_{L^{4} (Ω)}^{4} d s + c_{12} \sqrt{T} e^{c_{13} T} .$ (3.2)

下一步，我们估计积分 $\int_{0}^{t} {‖ \nabla a ‖}_{L^{4} (Ω)}^{4} d s$ 。利用Gagliardo-Nirenberg 不等式，在三维空间中我们有

$\begin{matrix} \int_{0}^{t} {‖ \nabla a ‖}_{L^{4} (Ω)}^{4} d s \leq \int_{0}^{t} (c_{14} {‖ Δ a ‖}_{L^{2} (Ω)}^{2} {‖ a ‖}_{L^{\infty} (Ω)}^{2} + c_{15} {‖ a ‖}_{L^{\infty} (Ω)}^{4}) d s \\ \leq c_{16} \int_{0}^{t} {‖ Δ a ‖}_{L^{2} (Ω)}^{2} d s + c_{17} t . \end{matrix}$ (3.3)

把(3.3)插入(3.2)，得到对任意 $0 < t \leq T$ ，成立

$\int_{0}^{t} {‖ \nabla ω \cdot \nabla a ‖}_{L^{2} (Ω)}^{2} d s \leq \sqrt{t} c_{18} e^{c_{19} T} \int_{0}^{t} {‖ Δ a ‖}_{L^{2} (Ω)}^{2} d s + \sqrt{T} c_{20} (1 + T) e^{c_{19} T} .$ (3.4)

把(3.4)插入(3.1)，得到对任意 $0 < t \leq T$ ，成立

$\int_{0}^{t} {‖ Δ a ‖}_{L^{2} (Ω)}^{2} d s \leq 2 ξ^{2} \sqrt{t} c_{18} e^{c_{19} T} \int_{0}^{t} {‖ Δ a ‖}_{L^{2} (Ω)}^{2} d s + A_{1} (T),$

其中 $A_{1} (T) = c_{8} T + c_{9} e^{2 ξ η T} + 2 ξ^{2} \sqrt{T} c_{20} (1 + T) e^{c_{19} T}$ 。

因此，

$(1 - 2 ξ^{2} \sqrt{t} c_{18} e^{c_{19} T}) \int_{0}^{t} {‖ Δ a ‖}_{L^{2} (Ω)}^{2} d s \leq A_{1} (T) .$

取 $t_{1} = \frac{1}{{(4 ξ^{2} c_{18} e^{c_{19} T})}^{2}}$ ，上式化为

$\int_{0}^{t} {‖ Δ a ‖}_{L^{2} (Ω)}^{2} d s \leq 2 A_{1} (T) .$ (3.5)

(1)如果 $t_{1} \geq T$ ，那么定理得证；

(2)如果 $t_{1} < T$ ，我们取 $t_{0} = t_{1}$ 作为初始时间，重复上述过程。因为 $t_{1}$ 仅仅依赖于T，通过有限步，我们可以将估计(3.5)延展到区间 $[0, T]$ 上，那么定理得证。

引理3.6：假设 $(a, υ, ω) \in {(C^{2, 1} (Q_{T}))}^{3} (T > T_{0})$ 是系统(1.2)的解，在三维空间中，对任意 $p > 2$ ，成立

$\int_{0}^{T} {‖ \nabla a ‖}_{L^{p} (Ω)} d t \leq A_{2} (T) .$

注意：在三维空间中( $n = 3$ )，利用Gagliardo-Nirenberg不等式，我们有

${‖ \nabla a ‖}_{L^{p} (Ω)} \leq {‖ Δ a ‖}_{L^{2} (Ω)}^{θ} {‖ \nabla a ‖}_{L^{2} (Ω)}^{1 - θ} + {‖ \nabla a ‖}_{L^{2} (Ω)},$

其中

$0 < θ = 3 (\frac{1}{2} - \frac{1}{p}) < 1, (p > 2) .$

利用Young不等式，椭圆 $L^{p}$ 估计( [10] 中推论9.10)，我们推出

$\begin{matrix} \int_{0}^{T} {‖ \nabla a ‖}_{L^{p} (Ω)} d t \leq \int_{0}^{T} {‖ Δ a ‖}_{L^{2} (Ω)}^{θ} {‖ \nabla a ‖}_{L^{2} (Ω)}^{1 - θ} d t + \int_{0}^{T} {‖ \nabla a ‖}_{L^{2} (Ω)} d t \\ \leq c_{21} \int_{0}^{T} {‖ Δ a ‖}_{L^{2} (Ω)} d t + c_{22} \int_{0}^{T} {‖ \nabla a ‖}_{L^{2} (Ω)} d t \\ \leq c_{23} \int_{0}^{T} {‖ Δ a ‖}_{L^{2} (Ω)}^{2} d t + c_{24} T + c_{22} \int_{0}^{T} {‖ \nabla a ‖}_{L^{2} (Ω)} d t \\ \leq A_{2} (T) . \end{matrix}$

引理得证。

4. 三维空间中的整体存在性

定理4.1：在三维空间中，在初始条件(1.3)成立的条件下，对任意 $T > 0$ ，系统(1.2)存在唯一的解满足 $(a, υ, ω) \in {(C^{2 + l, 1 + \frac{l}{2}} (Q_{T}))}^{3}$ 。

证明：利用反证法，取有限时间 $\tilde{T} > 0$ 。假设 $[0, \tilde{T})$ 是解存在的极大生命区间，我们取 $(a (x, \tilde{T} - ε), υ (x, \tilde{T} - ε), ω (x, \tilde{T} - ε))$ (其中 $0 < ε < \tilde{T}$ )作为一个新的初始值。利用延展定理，对 $T_{1} > 0$ ，我们

可以将解延拓至 $Q_{(\tilde{T} - ε) + T_{1}}$ 。而且根据定理3.1，我们知道 $T_{1}$ 仅依赖于 ${‖ a (x, \tilde{T} - ε) ‖}_{C^{2} (\bar{Ω})}$ ， ${‖ υ (x, \tilde{T} - ε) ‖}_{C^{2} (\bar{Ω})}$ ， ${‖ ω (x, \tilde{T} - ε) ‖}_{C^{1} (\bar{Ω})}$ 的上确界。因此通过先验估计 ${‖ (a, υ, ω) ‖}_{C^{2 + l, 1 + \frac{l}{2}} (Q_{T})} \leq A (T)$ ，我们知道 $T_{1}$ 依赖于 $\tilde{T}$ ，换句话说， $T_{1} = T_{1} (\tilde{T})$ 。因此，如果我们取 $ε < T_{1}$ ，那么 $(\tilde{T} - ε) + T_{1} > \tilde{T}$ ，从而产生矛盾。定理得证。

参考文献

[1]	Tao, Y. (2011) Global Existence for a Haptotaxis Model of Cancer Invasion with Tissue Remodeling. Nonlinear Analysis: Real World Applications, 12, 418-435. https://doi.org/10.1016/j.nonrwa.2010.06.027
[2]	Pang, P.Y.H. and Wang, Y.F. (2017) Global Existence of a Two-Dimensional Chemotaxis-Haptotaxis Model with Remodeling of Non-Diffusible Attractant. Journal of Differential Equations, 263, 1269-1292. https://doi.org/10.1016/j.jde.2017.03.016
[3]	Tao, Y. (2009) Global Existence of Classical Solutions to a Com-bined Chemotaxis-Haptotaxis Model with Logistic Source. Journal of Mathematical Analysis and Applications, 35, 460-469. https://doi.org/10.1016/j.jmaa.2008.12.039
[4]	Tao, Y. (2014) Boundedness in a Two-Dimensional Chemotaxis-Haptotaxis System. arXiv:1407.7382.
[5]	Tao, Y. and Winkler, M. (2011) A Chemotaxis-Haptotaxis Model: The Roles of Nonlinear Diffusion of Logistic Source. SIAM Journal on Mathematical Analysis, 43, 685-704. https://doi.org/10.1137/100802943
[6]	Tao, Y. and Winkler, M. (2014) Energy-Type Estimates and Global Solvability in a Two-Dimensional Chemotaxis-Haptotaxis Model with Remodeling of Non-Diffusible Attractant. Journal of Differential Equations, 257, 784-815. https://doi.org/10.1016/j.jde.2014.04.014
[7]	Tao, Y. and Winkler, M. (2014) Dominance of Chemotaxis in a Chemotaxis-Haptotaxis Model. Nonlinearity, 27, 1225-1239. https://doi.org/10.1088/0951-7715/27/6/1225
[8]	Tao, Y. and Wang, M. (2008) Global Solution for a Chemotactichaptotactic Model of Cancer Invasion. Nonlinearity, 21, 2221-2238. https://doi.org/10.1088/0951-7715/21/10/002
[9]	Wang, Y. (2016) Boundedness in the Higher-Dimensional Chemotaxis-Haptotaxis Model with Nonlinear Diffusion. Journal of Differential Equations, 260, 1975-1989. https://doi.org/10.1016/j.jde.2015.09.051
[10]	Ladyzenskaja, O.A., Solonnikov, V.A. and Uralceva, N.N. (1968) Linear and Quasi-Linear Equations of Parabolic Type. American Mathematical Society Translations, 23. https://doi.org/10.1090/mmono/023

为你推荐

友情链接