1. 引言
考虑到自然界中的随机扰动,在确定性模型的基础上,众多学者添加各种随机因素,构建更符合实际动力学性态的随机离散模型进行研究,在生物种群、流行病等方面取得了许多成果 [1] - [8] 。例如,Leonid-Shaikhet [6] 研究了一类带有对数的随机差分方程解的渐近行为,得到平衡点的稳定性条件;Peter Palmer [7] 使用Euler-Maruyama法将1-维随机方程线性化,应用伊藤公式研究随机差分方程解的稳定性;Anqi Miao [8] 等分析了一类随机SIS传染病模型,将确定性系统与随机系统进行比较,发现随机扰动有着不可忽视的影响。
在市场行为中,经济活动也会受到不同程度的随机干扰,然而目前动力系统在经济模型中的应用还处于初级阶段 [9] [10] [11] ,其模型建立及算法需要人们更进一步的探索和研究。本文研究一类差分方程经济模型,在一定随机干扰的影响下,模型平衡解的稳定性。
2. 建立模型
随着中国经济的飞速发展,各种新产品层出不穷,为了让它们更快地进入大众视野,广告成为一种重要的营销手段。许多学者致力于广告量-购物水平的研究 [12] [13] [14] ,然而他们大多忽略了经济活动中随机干扰这一因素。
首先,我们考虑下面传统的广告量-购物水平模型 [12] :
(1)
其中
、
、
是正系数,
表示t时刻的购物水平,
表示t时刻的广告投入量,
是最大购物水平,
是最大广告量;当广告量不超过一定额度时,随着广告投放量的增加销售量也会增加,当广告量超过一定额度时,可能会引起人们的逆反心理,广告量的增加反而会影响销售量。从方程(1)中我们容易求出系统存在两个平衡点
和
。
在市场行为中,各种随机因素也会影响广告的效果,因此本文对模型(1)引入随机干扰项,通过欧拉离散方法,得到下面的随机差分方程:
(2)
其中
表示随机干扰强度;n表示离散的时间,
,
;
表示相互独立的随机变量序列,且满足
,
,
。
考虑到模型的实际情况,本文中我们只讨论正平衡点的稳定性。令
,
,在平衡点
处,对模型(2)进行Jacobi线性化,得到下面线性方程:
(3)
显然,模型(2)正解的局部稳定性等价于模型(3)在零解处的稳定性。
设
,模型(3)可以写成下面这种形式:
(4)
其中:
,
3. 平衡点的稳定性
为了讨论方程(3)在零解处的稳定性,我们还需要下面一些定义与引理。
定义1. [15] 如果任意的
,存在
,使得对任意的初始函数
,有
,
,则称方程(3)的零解是均方稳定的;如果解是均方稳定的且对任意初始函数
,方程的解满足条件
,则称方程(3)的零解是渐近均方稳定的。
定义2. [16] 设P、Q均为实对称正定矩阵,若
也为实对称正定矩阵,即有
,则称P大于Q,记作
。
引理1. [15] 如果存在一个非负函数
满足下面的条件:
,
,
是正常数,
,那么方程(3)的解是渐近均方稳定的。
定理1. 对于一些二维正定矩阵P,矩阵方程:
(5)
解为半正定矩阵D,那么方程(3)的零解是渐近均方稳定的。
证明:首先我们构造一个Lyapunov函数:
其中
是一个半正定矩阵。
计算
的期望,我们可以得到下面的式子:
其中
。
因此:
其中
,c是一个大于零的常数。于是根据引理1,定理得证。
4. 数值模拟
由第2节中我们知道:
,
因此矩阵方程(5)可以写成下面这种形式:
,
,
其中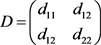 ,
。
,
。
理论上P和D存在多个解,在此我们只给出一个具体的例子。令
,
,
,
,平衡点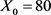 ,
,矩阵
,通过MATLAB计算可以得到一个正定矩阵P:
。
,
,矩阵
,通过MATLAB计算可以得到一个正定矩阵P:
。
根据定理1,方程(3)在零解处渐近均方稳定,因此方程(2)在正解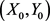 处是局部渐近均方稳定。设初值为
,通过数值仿真得到方程解的稳定性图像如下图1和图2。
处是局部渐近均方稳定。设初值为
,通过数值仿真得到方程解的稳定性图像如下图1和图2。
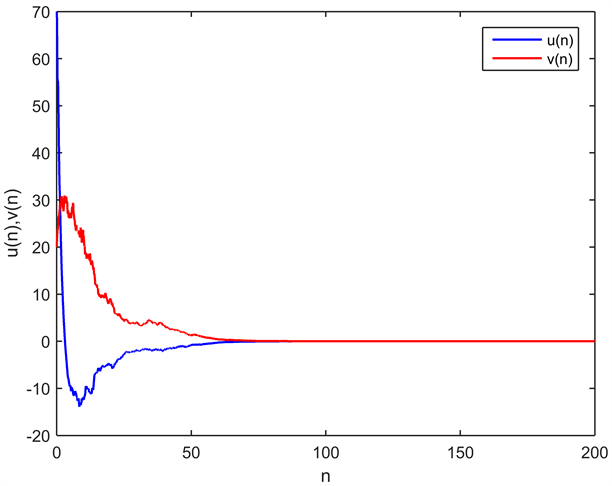
Figure 1. Asymptotically mean square stability of Equation (3) at the zero point
图1. 方程(3)在零点渐近均方稳定
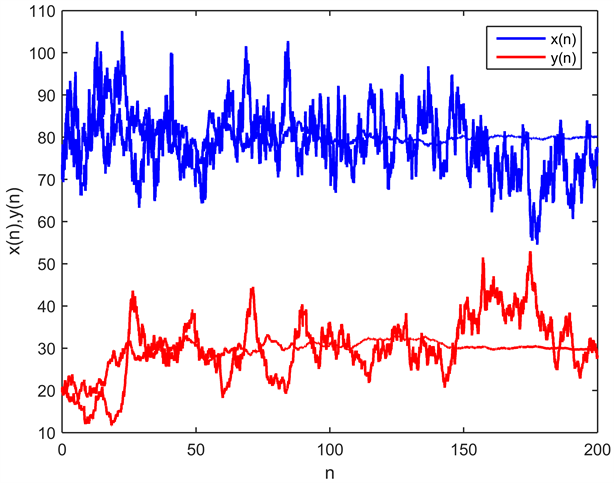
Figure 2. Asymptotically mean square stability of Equation (2) at the positive equilibrium point
图2. 方程(2)在正平衡点处局部渐近均方稳定
5. 总结
本文通过构造Lyapunov函数的方法研究一类随机经济模型解的稳定性问题。首先我们建立一个随机模型,经过欧拉离散化方法,得到了随机差分方程,然后将随机差分方程在正平衡点处线性化得到线性随机差分方程,证明当线性方程满足一定条件时,在零点处是渐进均方稳定的,由此得出方程在正平衡点处的局部渐进均方稳定性充分条件,并通过数值仿真验证了结论的正确性。本文研究的经济模型只考虑了随机扰动这一影响,如果还能得到方程解在时滞影响下的稳定性将更有现实意义,这也是我们今后所要研究的方向。
基金项目
湖南省自然科学基金(2016JJ2104)资助。
NOTES
*通讯作者。