1. 引言
本文中只限于讨论有限简单图。未给出的定义请参照文献 [1] 。设G和H是简单图,图
表示G与H的和,其顶点集为
,其边集为
。
设
是图G的一个二部划分,如果
,则称
是G的一个二部平衡划分。对于
,
表示两个端点都在
中的边的数目,
表示两个端点分别在顶点子集
中的边数。通常
用来表示平衡二部划分的大小。图G的一个最大(最小)平衡二部划分
是图G的所有平衡二部划分中
的值达到最大(最小)。与最大,最小平衡划分问题不同,公平划分问题是寻找图G的一个划分,使得多个分量同时进行优化。
本文将把图的公平划分问题变形到度序列的公平划分问题。
若简单图有顶点集
且
的度为
,则序列
称为G的度序列。记
为所有满足
的整数序列的集合。如果π是某个n阶简单图G的度序列,那么称π为可图序列,且G为π的一个实现。记
为
中的所有可图序列组成的集合。在可图度序列中,
表示有n个r,即度序列的实现中有n个顶点的度为r。
给定可图序列π,
是将π的元素划分为两部分后的两个子序列。如果
,则称
是π的一个平衡二部划分,其中
表示
中的元素数目。若G是π的一个实现,
是G的一个平衡二部划分且
在π中的度序列分别为
,则称
为π的平衡二部划分
的一个实现。
类似于图的“公平”划分问题,我们考虑度序列的“公平”划分问题:寻找已知可图序列π的一个平衡二部划分
,使得
的某个实现
在π的所有平衡二部划分的所有实现下
达到最大或者
达到最小,记
,
。若
是π的某个平衡二部划分的一个实现,显然
,
。
2. 主要定理及引理
定理2.1:(Erdös和Gallai [2] )设
且
是偶数。则
当且仅当对任意整数t,
都成立。
设
,
是两个非负整数序列。如果存在一个简单二部图
使得X和Y中的顶点度分别是
和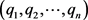 ,那么称序列对
,那么称序列对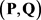 是二部可图的,并称二部图
是二部可图的,并称二部图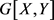 为
为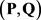 的一个实现。Gale [3] 和Ryser [4] 分别独立地给出了关于二部可图序列的刻划定理。
的一个实现。Gale [3] 和Ryser [4] 分别独立地给出了关于二部可图序列的刻划定理。
定理2.2:(Gale [3] , Ryser [4] ) 设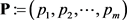 和
和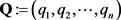 是两个非负整数序列且满足
是两个非负整数序列且满足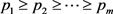 ,
,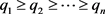 。若
。若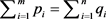 ,则
,则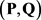 是二部可图的当且仅当
是二部可图的当且仅当
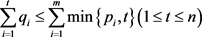
成立。
引理2.3:(Yin和Li [5] )设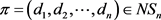 ,
, 且
且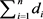 是偶数。如果
是偶数。如果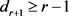 ,则
,则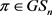 。
。
设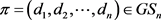 ,若
,若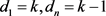 ,则称π是
,则称π是 -双正则可图的。本文主要给出双正则可图序列
-双正则可图的。本文主要给出双正则可图序列 的公平划分的上下界。
的公平划分的上下界。
3. (k, k − 1)-双正则可图序列的公平划分 的上界
的上界
定理3.1:设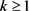 是一个正整数,m是4的整数倍且
是一个正整数,m是4的整数倍且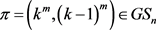 。那么
。那么
1) 若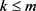 ,则
,则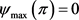 ;
;
2) 若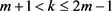 ,则
,则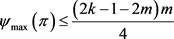 。
。
证明:情形(1):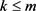 。
。
设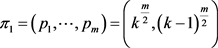 ,
,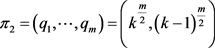 ,那么
,那么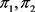 是π的一个平衡二部
是π的一个平衡二部
划分。这里,
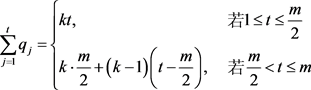 (1)
(1)
且
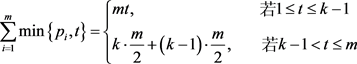 (2)
(2)
接下来我们比较 和
和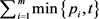 的大小。显然,由(1)和(2)得
的大小。显然,由(1)和(2)得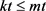 且
且
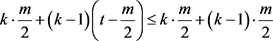 。
。
若 ,由(1)和(2)得,
,由(1)和(2)得,
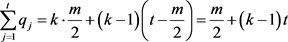 ;
;
 。
。
据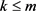 和
和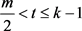 可得
可得
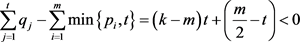 。
。
若 ,由(1)和(2)得,
,由(1)和(2)得,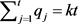 ;
;
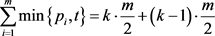 。
。
显然,
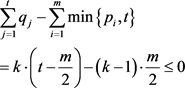 。
。
由定理2.2, 是二部可图的。设
是二部可图的。设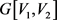 是
是 的一个实现,则G也是
的一个实现,则G也是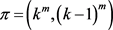 的一个实现且
的一个实现且 是G的一个平衡二部划分。因此,
是G的一个平衡二部划分。因此,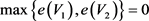 。
。
故,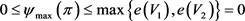 ,且
,且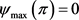 。
。
情形(2):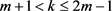 。
。
设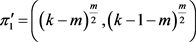 ,
,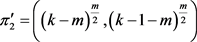 。由于
。由于 是偶数,所以
是偶数,所以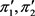 的度和
的度和 为偶数。由引理2.3知,
为偶数。由引理2.3知, 。设
。设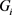 是
是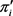 的一个实现且
的一个实现且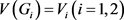 ,
,
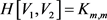 。令
。令 。容易验证G是π的一个实现,且
。容易验证G是π的一个实现,且
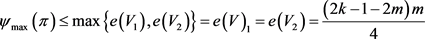 。
。
证毕。
4. (k, k-1)-双正则可图序列的公平划分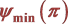 的下界
的下界
定理4.1:设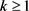 是一个正整数,m是4的整数倍且
是一个正整数,m是4的整数倍且 。那么
。那么
1) 若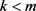 ,则
,则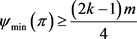 ;
;
2) 若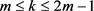 ,则
,则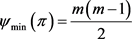 。
。
证明:情形(1):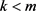 。
。
设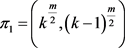 ,
,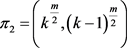 ,则
,则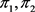 是π的一个平衡二部划分。由于
是π的一个平衡二部划分。由于 是偶数,所以
是偶数,所以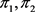 的度和
的度和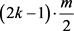 为偶数。又由引理2.3可得,
为偶数。又由引理2.3可得,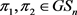 。设
。设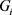 是
是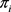 的一个实现且
的一个实现且
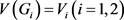 ,令
,令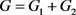 。容易验证G是π的一个实现,
。容易验证G是π的一个实现,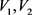 是G的一个平衡二部划分且
是G的一个平衡二部划分且
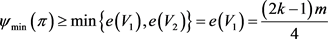 。
。
情形(2):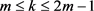 。显然
。显然 。
。
设 ,
,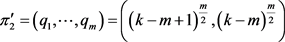 。这里,
。这里,
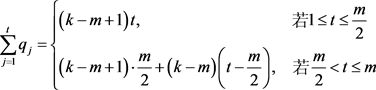 (3)
(3)
且
 (4)
(4)
接下来我们比较 和
和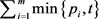 的大小。显然,由(3)和(4)得
的大小。显然,由(3)和(4)得 且
且
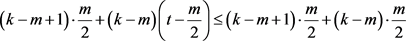 。
。
若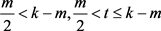 ,由(3)和(4)得,
,由(3)和(4)得,
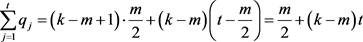 ;
;
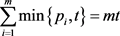 。
。
据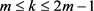 和
和 可知
可知

若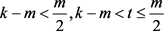 ,由(3)和(4)得,
,由(3)和(4)得,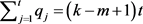 ;
;
 。
。
显然,
 。
。
由定理2.2,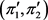 是二部可图的。设
是二部可图的。设 是
是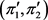 的一个实现,
的一个实现,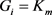 且
且 。令
。令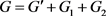 ,则G是
,则G是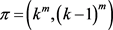 的一个实现且
的一个实现且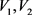 是G的一个平衡二部划分。故,
是G的一个平衡二部划分。故,
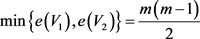 。
。
因此,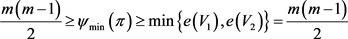 ,
,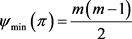 。证毕。
。证毕。
基金项目
海南省自然科学基金(No. 20161003, 20161002);国家自然科学基金(No. 11601108)。