1. 引言
柴油机是我国交通行业的主力机械,柴油机工作时承受负载大,故障发生概率大,其转子振动问题一直未得到有效解决,困扰着工程技术人员。国内外学者对故障模式识别的研究开展的较多,取得了一系列成果。文献 [1] 提出了一种新的多分类模式识别算法,用于解决大样本情况下的多类故障模式识别问题。但算法本身只精简了输入参数的个数,没能考虑参数间存在的关联。如果输入参数间存在耦合,识别精度将降低。并且算法本身涉及多重迭代,计算时间较长。文献 [2] 针对轴承早期故障特征难以提取的问题,提出了一种基于非线性流形学习的轴承早期故障诊断方法。将原始数据映射到线性可分的高维空间,消除了参数之间的关联,通过实例验证表明该方法提取的特征敏感性更好,提高了故障模式的识别能力,实现了轴承的早期故障诊断。文献 [3] 提出一种基于几何模式识别技术的发动机传感器故障诊断方法,但距离是定义在原始欧式空间上的,数据之间存在关联,不同类别分类存在交叠,识别效果不理想。文献 [4] 将粗糙集理论的属性约简与核主元分析方法结合起来,提出一种基于粗糙核主元分析的故障特征提取方法。利用核主元方法得到线性可分的特征参数,经粗糙集属性约简进一步得到最简的特征参数,提高了故障识别精度。
由于获取的柴油机转子振动数据量巨大,设计一种算法,只利用少量的代表点集就可以表征原始数据,极大的减小了计算量。利用数据代表点集的小波包提取振动信号能量特征,各个特征参数彼此独立;将小波包分解与粗糙集理论相结合,对转子不对中、支座松动和碰摩故障振动信号进行数据挖掘,获取了简化的识别规则。以获取的规则为基础,利用神经网络识别转子振动故障,使诊断规则具有泛化性,提高识别精度。在样本数据足够多的情况下,建立的粗糙集和神经网络故障诊断方法可以推广到其他机械装置,为转子振动信号监测、诊断和识别提供有意义的方法支撑 [5] 。
2. 故障模式识别
首先在获取的柴油机转子振动数据基础上,利用数据代表点集化简代替原始数据,大大减少计算量,进而计算原始数据代表点集的小波包,提取振动信息能量特征,将小波包分解与粗糙集理论相结合,利用粗糙集方法获取简化的规则。以获取的规则为基础,利用BP神经网络的方法诊断转子振动故障。基本思路如图1所示。
3. 数据代表点集
由于柴油机上安装的传感器采集的数据量巨大,极大的增加了计算量。因此需要对其进行化简,从大量的训练样本中提取一定量的具有代表性的数据集,这样减少了计算量,为此引入原始数据代表点集 [2] ,使数据代表点集能够完整的代替原始数据,不丢失重要信息。所谓数据代表点集即是均匀分布在样本中的稀疏点。获取代表点集设计的算法如下 [6] :
令
为样本
的e-邻域,它是以
为中心,以e为半径的超球,满足条件“任取
,
”。而
处的密度表示表示位于
中训练样本的个数,即
,其中
是样本集。进一步,如果P满足:
1)
;
2)
;
3)
。
则称P为样本X的代表点集。
定义
,为尚未考虑的样本集合。则生成样本代表点集P的伪代码如下:
(1)
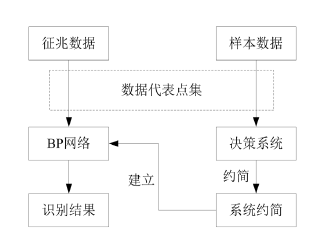
Figure 1. Fault pattern recognition based on rough set and neural network
图1. 基于粗糙集和神经网络的故障模式识别
初始阶段,设定
,
,进一步计算
,如果
,则认为x为代表点集,并且去除掉
中的点x,依次循环计算,直到
为空,这样就确定了X的代表点集P。同时,由于异常点与正常点定义的距离较远,不满足代表点集的邻域条件,这样就可以将代表点集的异常点排除,从而达到了消除异常点的作用。
4. 数据特征提取
原始数据代表点集确定后,对代表点集进行特征提取,增加输入特征的辨识性。小波包信号提取算法,按任意时频分辨率分解,将不同频段的信号正交分解到相应频段内。并根据先验知识,保留分解序列中任意一个或几个频段序列进行重构。小波包信号提取能量特征算法实现过程如下 [7] :
1) 选取适当的小波包函数,选取sym7小波;
2) 确定分解层数L,本文
;
3) 根据先验知识和每个序列的起始频率,计算出位于第L层的某几个频段内的频率成分;
4) 对数据进行逐层小波包分解。分解第l层时得到位于不同频段的
组序列。每组序列分别由低通滤波结果
和高通滤波结果
组成。
5) 利用回复公式重构信号。
利用小波系数的平方来计算小波包分解第j级分解水平上的第k个子频带上的平均能量,即
(2)
假定原信号按某一小波包分解树分解后由M个子频带组成,这M个子频带不一定都在同一级分解水平上。由能量守恒定律可知信号总能量等于各子频带能量之和,即
(3)
对式(3)的子频带的能量值进行能量归一化,得到
(4)
5. 粗糙集与数据离散化方法
粗糙集理论(Rough Set,RS)是一种用于处理不完整、不精确知识的数学方法 [8] [9] 。该理论能对数据进行分析和推理,并从中发现隐含的知识,揭示潜在的规律。因此利用粗糙集可以提取有用信息,简化原始数据。
粗糙集通过指定对象的基本特征(属性值)和对应的特征值(属性值)进行描述的,通常此种知识表达系统称为信息系统,表述如下:
是一个知识表达系统,其中U表示对象的非空有限集合,称为论域;
, ,C称为条件属性集,D称为决策属性集;
,
是属性a的值域;f表示
是一个信息函数,它为每个对象的每个属性赋予一个信息值,即:
。具有条件属性和决策属性的知识表达系统称为决策表。两个属性集C与D之间的依赖程度
定义为
,C称为条件属性集,D称为决策属性集;
,
是属性a的值域;f表示
是一个信息函数,它为每个对象的每个属性赋予一个信息值,即:
。具有条件属性和决策属性的知识表达系统称为决策表。两个属性集C与D之间的依赖程度
定义为
(5)
其中,
表示等价集
是属性集C下近似集的并集;
表示并集的元素个数;
表示整个对象集合的个数;g表示根据条件属性C的取值,能准确判断出属于某个决策属性D的等价集
的对象所占系统中整个对象的比例,即表示条件属性C能区分决策属性等价集的能力。
进一步,属性
在D中对D的重要度定义为:
(6)
其中,
表示在条件属性集C中缺少属性a后,条件属性与决策属性的依赖程度;
表示条件属性集C中缺少属性a后,导致不能被准确分类的对象在系统中所占的比例。如果重要度
的值越大,说明在已知P的条件下,属性a对于决策D越重要。
通过对振动特征数据结构特点分析,采取等频率离散法与公平尺度法相结合的离散方法进行划分 [10] [11] 。等频率离散法划分的过程为:将样本数据分成n段,每段有m个对象。根据每个属性的最大值、最小值及划分参数,将这个属性的所有数值从小到大进行排列,然后取间断点
和
,使得每两相邻断点之间所包含属性值的个数相等;采用公平尺度法划分的过程为:对每个属性
,根据
的值,对
进行由大到小的排序;从上到下扫描,设
和
代表两个相邻的实例:如果
,则继续扫描;如果
,即决策相同,则继续扫描;否则,得到一个断点
,
。即如果条件属性与决策属性都不同,那么选取两个条件属性值的平均值作为断点值。
得到约简的属性作为特征输入后,由于诊断规则不能完全涵盖所有故障样本,泛化性不强,这是粗糙集理论的一个局限。针对此情况,引入BP神经网络解决问题。考虑BP神经网络具有强大的映射能力和容错能力,建立特征输入与故障模式的非线性识别模型,增加故障模式识别系统的泛化能力。至此,本文确定的故障模式识别系统结构如图2所示。
6. 基于粗糙集和神经网络的故障模式识别
确定转子振动的转子不对中、支座松动和动、静碰摩故障等类型。在确定传感器采集的振动数据代表点集后,对代表点集进行特征提取。其中,抽取代表点集算法中的
密度
,半径
。
首先计算三种故障形式代表点集的小波包分解层次。在频域上对转子的几种典型故障进行分析,发现其振动频率多为基频、倍频及半频。根据这个规律,对包含这些特殊频率,特别是基频的频带进行更加细致的划分。确定小波包分解树如图3所示,将信号划分为13个频带,对几种转子振动故障类型都采用这个划分方法。这样划分既保证了按照每种故障的特征进一步放大特殊频带,又有统一的频带划分层次,以满足后续数据挖掘的要求。
以转子不对中故障为例,通过对转子不对中信号进行5级sym7小波的小波包分解,计算得到1至5层的细节信号能量特征以及第5层的低频信号能量特征,形成了
、
、
、
、
、
、
、
、
、
、
共11个频带的能量特征。用
表示原信号,
表示小波包分解第j层的第k个频带的信号的小波系数,小波包分解可表示为
(7)

Figure 2. System of fault pattern recognition
图2. 故障模式识别系统
依据小波包分解的层次和小波能量特征提取算法,进而得到不对中故障的各频段小波分解系数对应的频带和能量特征,见表1。
重复上述各个步骤,依次对支座松动及动静碰摩其他两种故障形式进行小波包的分解计算,得到相应故障的各频段小波分解系数的频带,按照小波包能量特征提取算法,进一步得到转子不对中、支座松动、动静碰摩等三种故障的能量特征,具体数据见表2。
根据表2数据结构的特点,采用将等频率划分和公平尺度法划分相结合的离散方法对决策表中的数据进行离散。根据表2中的分隔点与分隔区间,对表2中的条件属性
进行离散区间的划分。最终确定对条件属性
、 及
采用等频率划分法离散数据,对条件属性
、
、
、
、
、
、
及
采用公平尺度算法离散数据。
及
采用等频率划分法离散数据,对条件属性
、
、
、
、
、
、
及
采用公平尺度算法离散数据。
取60个振动信号样本数据进行分析。用归一化的能量特征作为条件属性,用故障类型作为决策属性形成故障的能量特征数据表。粗糙集要求有足够多的样本进行训练才能保证诊断的正确率,故取80%的数据作为训练样本,这里取每种故障样本的前16个样本(各个样本都是单独测试得到的,并无规律),取余下20%的数据作为测试样本。为了方便数据的运算,设定条件属性离散后的每一频段
的整数值域为0~n;d表示决策,d取值范围为0~2,即0代表转子不对中故障;1代表支座松动故障;2代表碰摩故障。删除条件属性相同的行。减少冗余样本,最终得到确定性规则。结果见表3。
当诊断规则确定后,如果接收检验的样本较少且条件属性都在建立的诊断规则内,粗糙集可以达到很高的精度,据此将剩余的20%作为测试样本接收检验。发现
,
不能得到有效的诊断,究其原因是训练样本建立的识别规则不能涵盖所有的故障样本,因此建立BP神经网络识别故障模式。经分析确定,BP神经网络输入神经元个数为2,中间层数为5,输出神经元个数为1。
1) 本文故障模式识别与其他方法对比
将本文模式识别方法与多分类SVM、k-means方法对比,将数据带入到三种模式识别系统中,结果见表4。
由表4可以看出,本文确定的故障识别方法精度最高,计算时间相对较少;多分类SVM方法将原始数据映射到高维可分空间中,但原始数据中存在信息冗余和干扰项,使得各分类边界模糊,降低了精度,同时向高维空间进行非线性映射,计算时间较长;k-means是一种线性分类方法,在原始参数线性空间构造各分类面,参数间不存在映射变换,计算用时较短,精度较低。

Table 1. The corresponding frequency bands and energy characteristics of wavelet packet decomposition coefficients of misalignment fault
表1. 不对中故障各频段小波包分解系数对应的频带和能量特征

Table 2. Data table of fault energy feature
表2. 故障的能量特征数据表

Table 3. Optimal fault diagnosis decision
表3. 最优故障诊断决策表

Table 4. Comparison of pattern recognition and other methods
表4. 本文模式识别和其他方法对比
2) 代表点集与原始数据特征提取模式识别对比
分别对原始数据与其代表点集进行特征提取,而后输入到确定的故障模式识别系统中进行识别。结果见表5。
由表5可以得出,代表点集较之原始参数特征输入,不论是在诊断精度还是计算用时,都明显优于对方。一般来讲,代表点集是原始数据的小部分数据,数量明显少于原始数据个数,同时又不丢失原始数据主要信息,所以计算用时较短。抽取代表点集过程中,有效的排除了异常点,这样在故障诊断中,就可以避免了异常点的干扰,提高了诊断精度。
3) 未经特征提取与特征提取后模式识别对比
分别对原始数据代表点集直接输入到BP神经网络以及代表点集特征提取后输入到识别系统中,进行故障识别。结果见表6。
由表6可以发现,代表点集直接输入到BP神经网络,跳过了特征提取等关键环节,虽然节省了时间,但代表点集经特征提取后,进一步得到了与模式识别最核心最相关的特征,同时经粗糙集处理,去除掉规则相悖与重复的特征,因而提高了诊断精度。
虽然确定的故障模式识别系统极大的提高了识别精度。但从表4、表5和表6可以看出,仍然存在识别错误的样本,说明输入的特征数目不足以准确识别故障。在BP神经网络输入前,在粗糙集确定的诊断规则前增加条件属性,经分析确定增加条件属性
,因此新确定的诊断系统为
,重新带入到BP神经网络(此时,输入神经元个数为3个,中间层数为5,输出神经元个数为1)中,诊断精度达到100%。
7. 总结
本文设计了“原始数据代表点集 + 小波分解特征提取 + 粗糙集理论 + BP神经网络”的故障识别系统,较好地解决了柴油机转子振动系统故障模式识别问题。得到的主要结论如下:
1) 本文设计的故障识别系统达到了很高的精度。选取了原始数据代表点集,极大的减少了计算量,同时代表点集又可以表示原始数据全部信息,可以达到很高的诊断精度。
2) 代表点集经过特征提取和粗糙集处理后,能够得到最简化的最直接的与故障相关的特征,诊断精度大为提高。并且本文故障识别系统与SVM多分类与k-means识别方法相比,计算用时与精度都有所提高。
3) 以最简化的诊断规则作为输入,带入到BP神经网络中,不能涵盖所有故障样本,此时增加条件属性数量,带入到神经网络输入中,可以提高识别断精度。

Table 5. Comparison of representative point and original data
表5. 代表点集和原始数据输入的结果对比

Table 6. Comparison of representative point direct input and feature extraction
表6. 代表点集直接输入和特征提取输入结果对比
致 谢
感谢孙涛博士在论文撰写中所给的技术和数据支持。