1. 引言

车辆在行驶过程中，总是选择最短路径行驶。根据交通流理论，可以建立车速与交通流量和密度之间的关系，进而得出描述路段行驶时间的路权。根据路段路权，可以采用最短路径的算法求得源点到终点的最少旅程时间路径。然而因各种突发事件(交通事故、自然灾害或交通管理等)造成道路中断的现象普遍存在，车辆在行驶的过程中并不具有道路中断的完全信息，只有行进到中断处时才获得道路中断的信息，此时原来的最短路径就很可能失去其最优性，从而增加交通运输的成本。国外从20世纪90年代开始，对道路模糊最短路路径算法展开研究，随后的研究集中于从旅程时间随机性和动态性角度计算期望最短路径(Expected Shortest Path) [1] 。国内最近几年也展开了对道路可靠性的研究，在道路连通、容量和畅通可靠性方面取得一系列成果 [2] [3] 。但这些方法给出最短路径的同时，没有给出合理的模糊风险率。本文应用模糊集理论，提出一种非完全动态信息条件下基于风险估计的行车诱导方法。该方法可以给出与模糊可靠度相对应的最短路径，供司机按实际情况决策使用，模糊可靠度在一定程度上反映了决策者的决策风险。

2. 模糊事件风险率理论

1975年Kaufmann首次应用模糊数学处理可靠性问题 [4] ，引入了可能性来表示元件的可靠性，但并未系统阐述其可能性，也没有给出明确的物理定义。Brown提出了结构模糊安全测度的概念，用模糊集合理论来表示结构的可靠性 [5] ；Wang Juite提出了一种随机模糊可靠度的分析方法 [6] 。下面主要以模糊事件为例介绍模糊风险分析理论。假设事件A为一模糊事件，A的特征函数就可以利用其隶属函数来表示，则模糊事件A的概率可以定义为：

$P\left(A\right)={\displaystyle {\int }_U{\mu }_A\left(x\right)\text{d}P}=E\left[{\mu }_A\left(x\right)\right]$ (1)

式中积分为L-S (H. Lebesgue)积分。若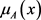和 $f\left(x\right)$ 是实数域R上的可积函数，则模糊事件概率为：

$P\left(A\right)={\displaystyle {\int }_U{\mu }_A\left(x\right)f\left(x\right)\text{d}}x$ (2)

式中： $f\left(x\right)$ 为随机变量X的概率密度函数， ${\mu }_A\left(x\right)$ 为模糊事件A的隶属函数，表示x隶属于模糊事件A的程度。

如果以模糊逻辑的方式来描述事件或者灾害的发生，那么可将该事件的失效状态作为模糊数来计算。假设一个系统的负荷为L，阻抗为R，且L和R均用模糊数表示。该系的可靠度或失效度可由负荷及阻抗的差值来描述，这时可靠度或失效度本身也是一个模糊数，为：

$Z=R-L$ (3)

取其h水平区间为： $R\left(h\right)=\left[R_1\left(h\right),R_2\left(h\right)\right]$ 和 $L\left(h\right)=\left[R_1\left(h\right),R_2\left(h\right)\right]$ 。那么，对于给定一个 $h\in \left[0,1\right]$ ，以 $R\left(h\right)$ 与 $L\left(h\right)$ 的差值便可以得出安全余量Z(h)，也称系统的工作状态。即：

$Z=R\left(h\right)-L\left(h\right)$ (4)

则 $Z\left(h\right)<0$ 表示为失效状态； $Z\left(h\right)=0$ 表示为极限状态； $Z\left(h\right)>0$ 表示为安全状态。系统的失效概率为 $P_r=P\left(Z\left(h\right)<0\right)$ ；系统的可靠度为 $P_r=P\left(Z\left(h\right)>0\right)$ 。

降半梯形分布是运用最为广泛的分布，以模糊失效状态A的隶属函数为降半梯形分布为，讨论突发事件引起道路交通拥挤风险率计算方法，其函数形式见式(5)。模糊失效状态A的隶属函数表达式为状态变量Z服从正态分布时，其分布密度函数见式(6)：

${\mu }_A\left(z\right)=\{\begin{array}{l}1,z<a\\ \left(b-z\right)/\left(b-a\right),a\le z\le b\\ 0,z>b\end{array}$ (5)

$f\left(z\right)=\frac{1}{\delta \sqrt{\text{2π}}}\exp \left(-{\left(z-\mu \right)}^2/2{\delta }^2\right)$ (6)

则模糊失效风险率的计算公式为：

$\begin{array}{c}{P}_r=P\left(A\right)={\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}{\mu }_A\left(z\right)f\left(z\right)\text{d}z}\\ ={\displaystyle \underset{-\infty }{\overset{a}{\int }}\frac{1}{\delta \sqrt{\text{2π}}}\exp \left(-{\left(z-\mu \right)}^2/2{\delta }^2\right)\text{d}z}\\ +{\displaystyle \underset{a}{\overset{b}{\int }}\frac{b-z}{b-a}\frac{1}{\delta \sqrt{\text{2π}}}\exp \left(-{\left(z-\mu \right)}^2/2{\delta }^2\right)\text{d}z}\end{array}$ (7)

式中的积分可以采用梯形积分进行数值计算。式(7)在计算失效风险率时，既考虑失效事件的模糊性又考虑其随机性。如果式中的Z表示为道路交通拥挤状态函数，假设当Z > 0时，道路状况达到要求；若Z < 0，道路交通拥挤，交通状态处于失效状态，则 $P_r$ 为道路交通拥挤模糊风险率。因此，式(7)为道路交通拥挤状态超标模糊随机风险率的计算模型。下面主要讨论计算模型的计算方法，并结合实例讨论基于风险估计的路径诱导方法。

3. 基于风险估计模糊最短路求解模型

由式(5)、(6)和式(7)可知，只要已知模糊隶属函数中的a与b，便能够获得道路上突发事件的模糊可靠度和模糊失效率。但是，隶属函数特征值a与b一般是根据主观经验法或扩增系数法来确定，两种方法均带有很强的主观性和经验性。同时在实际工程中，由于专家经验获取的不易，或是由于条件所限，难于进行实验及各项可信的数值统计，故其取值及验证均不容易，使模糊可靠度计算的推广具有较大的困难 [7] 。为解决这一问题，引入熵理论，意在不依靠主观性和经验性的前提下，在进行道路交通拥挤模糊风险率数值计算时，对a与b的取值范围给予定量的描述 [8] 。

本文主要讨论连续模糊事件的熵。对于样本空间 $\Omega =\left\{x_1,x_2,\cdots ,x_n\right\}$ 是有限集，其中X基本事件的概率密度函数为 $f\left(x\right)$ ，A为模糊事件，其隶属函数为 ${\mu }_A\left(x\right)$ ，模糊事件A概率为 [9] ：

$P_r=P_r\left(A\right)={\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}{\mu }_A\left(x\right)f\left(x\right)\text{d}}x$ (8)

连续模糊事件的熵可定义为 [10] ：

$H_r\left(A\right)=-{\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}{\mu }_A\left(x\right)f\left(x\right)\log \left({\mu }_A\left(x\right)f\left(x\right)\right)\text{d}}x$ (9)

因此，模糊事件的模糊熵 $H_r\left(A\right)$ 表示模糊事件A的不肯定程度。

式(9)的积分可以用式(7)代入后进行数值计算。

$\begin{array}{c}{H}_r\left(A\right)=-{\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}{\mu }_A\left(x\right)f\left(x\right)\log \left({\mu }_A\left(x\right)f\left(x\right)\right)\text{d}}x\\ =-{\displaystyle \underset{-\infty }{\overset{a}{\int }}\frac{1}{\delta \sqrt{\text{2π}}}\exp \left(-{\left(z-\mu \right)}^2/2{\delta }^2\right)\log \left(\frac{1}{\delta \sqrt{\text{2π}}}\exp \left(-{\left(z-\mu \right)}^2/2{\delta }^2\right)\right)\text{d}}x\\ -{\displaystyle \underset{a}{\overset{b}{\int }}\frac{b-z}{b-a}\frac{1}{\delta \sqrt{\text{2π}}}\exp \left(-{\left(z-\mu \right)}^2/2{\delta }^2\right)\log \left(\frac{b-z}{b-a}\frac{1}{\delta \sqrt{\text{2π}}}\exp \left(-{\left(z-\mu \right)}^2/2{\delta }^2\right)\right)\text{d}x}\end{array}$ (10)

采用式(9)便可以事先设置可接受的程度水平，对模糊隶属函数的特征值进行定量化分析，根据熵值判断和估计隶属函数中的a、b的取值是否合适，也可以采用多元函数求极值的方法确定a、b的取值。

4. 实例分析

萧山机场高速公路由于从地面快速路改为高架快速路，2014年4月起至2016年5月进行封闭施工，图1为机场高速周边路网拓扑图，1代表机场高速封闭起点，5代表机场，1-5的虚线代表机场高速封闭施工，因此只能其他的道路进行分流，由图1可知由源点1到终点5共有5条路径，分别是1-3-5，1-3-2-4-5，1-2-3-5，1-4-5和1-2-4-5。

用本文提出的模糊随机风险率方法对图1中的进行风险分析，各个点之间路径参数如表1所示：

道路交通流状态函数为：

$Z\left(X\right)=v_0-q/\left(k_1\cdot k_2\cdot k_3\cdot k_4\cdot c_0\right)$ (10)

式中：v₀为道路交通饱和度阀值，取值范围在0.8~1.0之间；k₁为非机动车影响系数；k₂为车道宽度修正系数；k₃为车道数修正系数；k₄为交叉口修正系数；q为道路交通量(pcu/h)；c₀为道路交通通行能力(pcu/h)。

当 $Z\left(X\right)\ge 0$ 时，道路交通环境质量达到要求；若 $Z\left(X\right)<0$ ，则道路交通环境超过控制目标，道路交通质量超标模糊随机风险率的计算与结果分析如下：

1) 状态变量均值及方差。交通环境状态参数特征值 ${\mu }_q$ ， ${\mu }_{k_1}$ ， ${\mu }_{k_2}$ ， ${\mu }_{k_3}$ ， ${\mu }_{k_4}$ 均为随机变量，且这些参数相互独立，按照随机变量运算法则，状态变量的均值可由下式(11)进行近似计算。

${\mu }_Z=v_0-{\mu }_q/\left({\mu }_{k_1}\cdot {\mu }_{k_2}\cdot {\mu }_{k_3}\cdot {\mu }_{k_4}\cdot c_0\right)$ (11)

将表1中各参数的特征值代入式(11)中，求得状态变量的均值 ${\mu }_Z=1.994$ ，标准差为 ${\delta }_Z=1.374$ 。

2) 隶属函数特征值的确定和模糊风险率的计算。以1-3-5路径为例，若隶属函数为梯形分布形式且Z的分布密函数已确定，式(9)中只有a、b二个变量，但直接采用多元函数求极值的方法确定 $H_r$ 的极大值及相应的a、b值十分困难，本文用数值方法进行近似求解。首先尝试性地限定 $a=0~\text{2}{\delta }_Z$ ； $b=0~\text{3}{\mu }_Z$ ，用MATLAB作出a-b-P_r曲线和a-b-H_r曲线。从图2和图3可见，当隶属函数确定后，其特征值a和b的取值对风险率有较大影响，因此采用模糊理论计算风险率时，合理确定特征值是关键。a的取值越小， $H_r$ 越大，当a < 0.115后，a继续减少， $H_r$ 的变化不显著，特别a < 0.110后， $H_r$ 的变化不大且P_r基本保持稳定；由图1可见，当a取值一定时，b-H_r曲线是上凸的曲线，即H_r存在最大值；在a取值变化过程中，对应 $H_r$ 的最大值的b值变化不大。因此在实际应用中采用梯形隶属函数时，可事先确定b的取值，而后确定a值。

3) 在本例中 $a=0.\text{1}{\delta }_Z$ 是可以接收的。以1-3-5路径为例，取a = 0.1374，当b = 2.792时， $H_r$ 取得最大值为1.107，此时对应的道路交通质量超标风险率为25.46%。依次计算各个路径的风险率如下表2。

由图1可知由源点1到终点5共有5条路径，分别是1-3-5，1-3-2-4-5，1-2-3-5，1-4-5和1-2-4-5，其路径长度分别是16，16，16，15和10。表2列举了路径1、路径2与路径3、4、5长度和 $a=0.\text{1}{\delta }_Z$ 时相应风险率的计算结果。如果不考虑风险率，则编号4的路径(1-4-5)为最短路；如果考虑风险率不超过30%的情况下，则编号1路径和编号3路径符合要求，但编号3路径风险率小于编号1，则编号3路径为基于风险估计的最短路径，在行车诱导时可给出编号3的路径。

5. 结语

论文针对我国非完全动态信息的现状，提出了基于风险估计的路径诱导方法，通过模糊事件概率理论和随机理论相结合的办法对道路进行风险估计。利用模糊事件概率理论计算道路饱和度超标风险率时，

确定隶属函数的特征值是一个很关键的问题，本文采用熵理论，通过描述隶属函数的特征值与模糊风险率的不肯定程度关系，可以不完全依靠经验的前提下合理确定隶属函数特征值，并计算出风险率。实践证明隶属函数形式的选择对风险率的计算也有一定影响，如何更合理的选择隶属函数形式用于道路饱和度超标风险计算模型有待进一步研究。

参考文献