1. 引言
对于社会网络重要性及其外部性的研究最早出现在经济领域。1984年Farrellhe 和Saloner在 [1] 一文中提到,在非完全信息网络中,可以通过外部性影响做出改革,从而找到更好的协调机制,替代原来的商品定价标准;1985年,Katz和Shapiro在 [2] 中进一步阐明了消费正外部性的存在,从而使得对商品的外部性有了更明确的定位。至此,外部性商品定价问题开始引起大家的注意。2008年,Hartline和 Mirrokni在 [3] 中首次从网络定价方面探讨商品扩散问题。他们发现:在允许区别定价的条件下,对于“目光短浅”的消费者,通过网络的正外部性影响及压榨式的定价方式,能够在全信息的社会网络中找到近似的最优营销策略(定价方案)。2010年,Akhlaghpour,Ghodsi和Haghpanah在 [4] 中首次介绍了正外部性商品的交互式定价,并构建了两个交互式定价模型。2011年,Chen, Lu, Sun, Tang, Wang和Zhu在 [5] 中讨论研究了非完全信息社会网络中,正外部性商品如何运用营销策略使得商家的利益最大化。2011年,Bhattacharya,Kulkarni,Munagala and Xu在 [6] 中证明了即使在树状网络图中,找到最优均衡依然是NP难的。2013年,Alon,Mansour,和Tenneholtz [7] 研究了区别定价造成消费者不公平心理所带来的负外部性。2014年和2017年,Cao,Chen,Hu and Wang [8] [9] 证明了找到最优定价的问题是NP难的,并且给出一些近似算法,对负外部性商品的定价进行了非常深入的研究。
本文主要是在 [9] 的基础上重新构建IPE (Iterative Pricing with Externalities)商品定价模型,进一步研究双重外部性影响下的商品定价问题。这里,我们同时考虑网络中的正负外部性。负外部性是指相关的消费者间,购买行为会降低未购买消费者对该商品的价值预估,正外部性影响则相反,会增加未购买消费者对该商品的价值预估。我们希望能找到定价策略,使得商家的收益达到最大化。
在第二节我们给出了IPE模型的介绍。在第三节我们证明了对IPE问题找到最优定价是NP难的,并且在星状网络图中给出了最优的交互式定价方案以及最大收益。在第四节我们证明了在星状网络图中,通过单一定价能得到近似比为2的定价策略。
2. 模型介绍
社会网络图
是一个简单图,
是表示所有节点(消费者)的集合,
是表示所有消费者关联的边集合,其中消费者间的相互影响力(外部性影响力)用边的权重表示,并做如下规定:对
,记权函数为
,当且仅当
时,
;默认相互间的影响力相同,即
;若
之间的外部性影响是正的,则
,且
;反之,则
,且
,记
,我们用
表示
在
所占比例,即
。
对任意消费者
,及任意消费者群体
,消费者
在群体
中受到的外部性影响等于
与
中所有关联边的权重之和,记为
。若图G不计权重,则
。
另外,消费者
的商品固有价值,我们记为
。在定价的过程中,消费者根据
时刻的定价决定是否购买该产品,我们规定:每一次定价后未购买该商品的消费者群体
,那么对任意消费者
,此刻该商品的总价值等于固有价值与外部性影响之和,即
,在给定的图
中,所有消费者的商品总价值都不小于0,也就是说,对于
,
。
显然,初始值
,IPE模型如下进行:
l 交互式定价:商家按时公布价格,在一个时间序列下给出对应的价格序列;
l 消费者是冲动的:当商品的定价低于消费者的预估价值,消费者第一时间会购买;
l 商家是贪婪的:当该商品对消费者的总价值增加时,商家随时会涨价;
l 同步购买:新的定价一经公布,所有消费者会第一时间做出选择,购买或放弃;
给定时间序列
,对应价格序列
,
时刻的定价记
,对任意的
,我们定义
为
时刻以
价格购买该商品所有消费者群体,
是通过第
轮销售商家所获得的收益,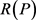 是在价格序列
是在价格序列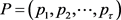 的定价下商家所获得的收益,即
的定价下商家所获得的收益,即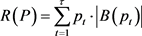 。在单一定价时,
。在单一定价时, ,我们通常用
,我们通常用 表示
表示 。为了方便起见,我们也用
。为了方便起见,我们也用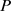 表示价格的集合
表示价格的集合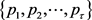 ,用标号
,用标号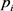 表示价格序列
表示价格序列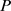 中一项。
中一项。
值得注意的是, 中的消费者若在
中的消费者若在 时刻未消费,可能会在
时刻未消费,可能会在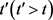 时刻以更高的价格购入该商品。直到所有消费者都购入,商家停止定价,此时
时刻以更高的价格购入该商品。直到所有消费者都购入,商家停止定价,此时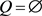 。
。
通常,我们用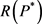 表示最佳收益,在不赋权且内在价值统一为
表示最佳收益,在不赋权且内在价值统一为 的情况下,我们也会用
的情况下,我们也会用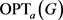 来表示最佳收益。
来表示最佳收益。
所谓IPE问题就是找到一个定价序列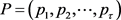 使得
使得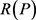 达到最大值,其中序列长度
达到最大值,其中序列长度 ,以及每一序列项
,以及每一序列项 都是可确定的。当
都是可确定的。当 取到0时,只考虑正外部性影响;当取到1时,只考虑负外部性影响,即是IPN问题。
取到0时,只考虑正外部性影响;当取到1时,只考虑负外部性影响,即是IPN问题。
3. 交互式定价
定理1 [8] 对于IPN问题,计算出最优定价序列不仅在一般网络图上是NP难的,即使是在不带权且内在价值都为 的树状网络图中也不例外。
的树状网络图中也不例外。
事实上,IPN问题是IPE问题在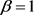 时的一种特殊情况,显然IPE问题也是NP难的。所以我们有下面的推论。
时的一种特殊情况,显然IPE问题也是NP难的。所以我们有下面的推论。
推论2 对于IPE问题,计算出最优定价序列不仅在一般网络图上是NP难的,即使是在不带权且内在价值都为 的树状网络图中也不例外。■
的树状网络图中也不例外。■
本节讨论在不带权且内在价值都为 的星状网络图中,我们如何通过多次定价使得收益最大化。
的星状网络图中,我们如何通过多次定价使得收益最大化。
定理3 图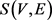 是以
是以 为中心点的不带权星状网络图中,若
为中心点的不带权星状网络图中,若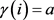 ,点集
,点集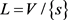 ,且
,且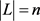 ,那么
,那么 。
。
证明:如图1,令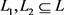 ,满足对
,满足对 ,
,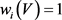 ,对
,对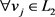 ,
, 。已知
。已知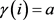 ,易得:对
,易得:对 ,
, ,对
,对 ,
,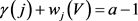 ,且对中心点
,且对中心点 ,满足
,满足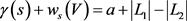 。根据定义可知,
。根据定义可知,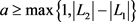 ,下面依据
,下面依据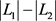 的大小进行分类讨论,其中
的大小进行分类讨论,其中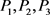 分别表示不同的定价方案。
分别表示不同的定价方案。
情形1
这种情况下,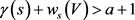 ,其中
,其中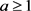 。此时我们需要讨论三种方案:
。此时我们需要讨论三种方案:
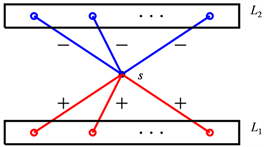
Figure 1. A star network with externalities
图1. 具有外部性的星状网络图
l 方案:
方案: ,
, ;
; ,
,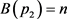 ;
; ;
;
l 方案:
方案: ,
, ;
;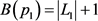 ,
, ;
; ;
;
l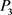 方案:
方案: ,
, ;
;
故 是最佳方案,可获得收益
是最佳方案,可获得收益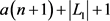 。
。
情形2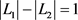
这种情况下,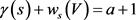 ,其中
,其中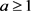 ,根据情形1的讨论易得:对于情形2,只用考虑情形1的后两种方案,显然最佳方案还是
,根据情形1的讨论易得:对于情形2,只用考虑情形1的后两种方案,显然最佳方案还是 ,可获得收益
,可获得收益 。
。
情形3
这种情况下,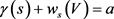 ,其中
,其中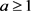 。此时我们需要讨论三种方案:
。此时我们需要讨论三种方案:
l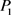 方案:
方案: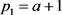 ,
,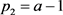 ,
,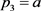 ;
;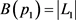 ,
,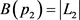 ,
, ,
, ;
;
l 方案:
方案: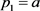 ,
, ;
; ,
,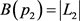 ,
, ;
;
l 方案:
方案: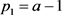 ,
, ;
;
故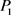 ,
, 是最佳方案,可获得收益
是最佳方案,可获得收益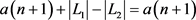 ;
;
情形4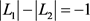
这种情况下,有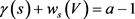 ,其中
,其中 ,根据情形3的讨论易得:对于情形4,只用考虑情形1的
,根据情形3的讨论易得:对于情形4,只用考虑情形1的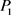 ,
,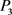 方案,显然最佳方案是
方案,显然最佳方案是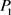 ,可获得收益
,可获得收益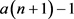 ;
;
情形5
这种情况下, ,其中
,其中 。此时我们需要讨论三种方案:
。此时我们需要讨论三种方案:
l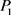 方案:
方案: ,
,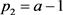 ,
,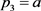 。
。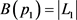 ,
, ,
,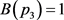 ,
,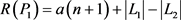 ;
;
l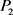 方案:
方案: ,
, 。
。 ,
,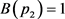 ,
,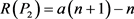 ;
;
l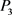 方案:
方案: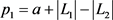 ,
, ;
;
故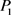 是最佳方案,可获得收益
是最佳方案,可获得收益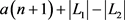 。
。
综上所述,当 ,商家的最大收益是
,商家的最大收益是 ;当
;当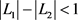 ,商家的最大收益可以达到
,商家的最大收益可以达到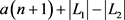 。由定义可知,
。由定义可知,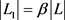 ,由此可得
,由此可得
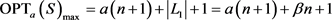 . ■
. ■
4. 单一定价
定理3中我们已经证明了,对于星状网络图,通过多次定价能达到最优值,同时也给出了相应的最大收益。事实上,很多时候商家销售某商品都是进行统一固定的定价,很自然地,我们会思考:在单一定价下,商家是否依然能够获得比较好的收益呢?本节我们将证明,在星状网络图中,运用单一定价也能得到好的近似。
引理4 [8] 在不带权且不含孤立点的森林状网络图上,若每个点的固定价值相等,则能获得最大收益的单一定价是对IPN问题的1.5-近似的解决方案。
定理5 在不带权的星状网络图上,若每个点的固定价值都为 ,则存在近似比为2的单一定价策略用以解决IPE问题。
,则存在近似比为2的单一定价策略用以解决IPE问题。
证明 图 是不带权的星状网络图,
是不带权的星状网络图,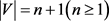 ,且每个点的固定价值都为
,且每个点的固定价值都为 ,只要取
,只要取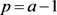 或
或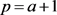 ,那么得到的收益一定大于
,那么得到的收益一定大于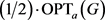 。
。
当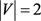 时,结论是平凡的。下面考虑
时,结论是平凡的。下面考虑 。
。
当 时,
时,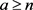 ,令
,令 ,则
,则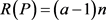 ,由定理3可知,最大收益
,由定理3可知,最大收益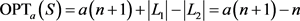 ,故
,故
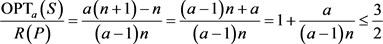
当 时,根据引理4可知,能找到近似比为3/2的单一定价策略,令
时,根据引理4可知,能找到近似比为3/2的单一定价策略,令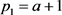 ,则
,则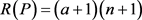 ,由定理3可知,
,由定理3可知,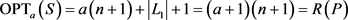 。
。
下面考虑 且
且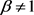 时,令
时,令 ,
, ,则
,则 。
。
若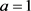 ,则
,则 ,根据定理3,当
,根据定理3,当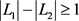 时,能获得的最大收益是
时,能获得的最大收益是 ,令
,令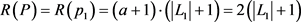 ,则
,则
 .
.
当 时,
时, ,令
,令 ,则
,则 .
.
若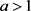 ,我们分4种情形进行讨论。
,我们分4种情形进行讨论。
情形1
则 ,
,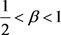 ,令
,令 ,有
,有
 .
.
情形2
则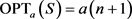 ,若
,若 ,那么
,那么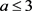 ,因此
,因此 ;若
;若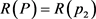 , 那么
, 那么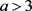 ,
,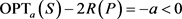 。
。
情形3
则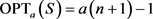 ,当
,当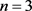 ,令
,令 ,则
,则 ,当
,当 时,令
时,令 或
或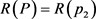 ,都满足
,都满足 。
。
情形4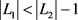
则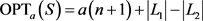 ,且
,且 ,
,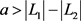 ,若
,若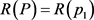 ,那么
,那么 ,因此
,因此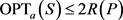 ,若
,若 ,依然满足
,依然满足 。
。
综上所述,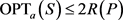 。 ■
。 ■
致谢
感谢朱绪鼎教授对本文的帮助,也感谢所有匿名审稿人对本文的指导意见。
基金项目
国家自然科学基金项目资助(CNSF 00571319)。