1. 引言
全社会固定资产投资是指某个国家或者地区内固定资产投资的数量和范围,建造和购置固定资产的经济活动,即固定资产再生产活动,是反映建设规模的综合性指标 [1] 。在国民经济发展过程中,社会固定资产投资是影响经济增长的一个重要因素,对经济增长具有直接的拉动作用。历来,许多学者从各方面证实了这一点,全社会固定资产投资与经济增长的彼此拉动也是实际数据的彰显。早期,学者胡春和仲继银就利用1981~1999的国内固定资产投资的数据,在《我国固定资产投资与经济增长周期关系的实证分析》中,通过建立固定资产投资的增长率与国内生产总值增长率间相关关系的回归模型,论证了固定资产投资对经济增长的推动作用。学者熊兴在《关于甘肃省固定资产投资与经济增长关系的实证研究》文中,就利用甘肃省1978~2011年的数据,从三次产业的角度分别论证了固定资产投资对经济增长的不同拉动作用。在《中国固定资产投资与经济增长相互动态决定的实证研究》中,作者龚曙明就运用回归模型研究了固定资产投资对经济增长的动态推动效应。大量论证表明了固定资产投资与经济增长的拉动作用,因此利用最新的数据研究全社会固定资产投资状况对经济发展具有非常重要的指导意义。全社会固定资产投资的实证分析大多运用时间序列分析方法,文章运用ARIMA模型进行河南省全社会固定资产投资的时间序列分析,从统计分析角度研究河南省历年固定资产投资的发展状况。
2. 序列的平稳性检验
2.1. 原序列的平稳性检验
文章数据来源于《2015河南省统计年鉴》,选取1989年~2014年河南省全社会固定资产投资总额为指标
。运用EVIEWS软件绘制原始数据的时间序列图,如图1所示,从图中可观察到该序列呈指数分布,初步判断
是一个非平稳的时间序列。
文章运用ADF检验来检验序列的平稳性,ADF检验法的基本原理是通过n次差分的方法将原始的非平稳序列转化为平稳序列,对ADF检验,检验统计量是检验回归滞后因变量的t统计量,由于是单边
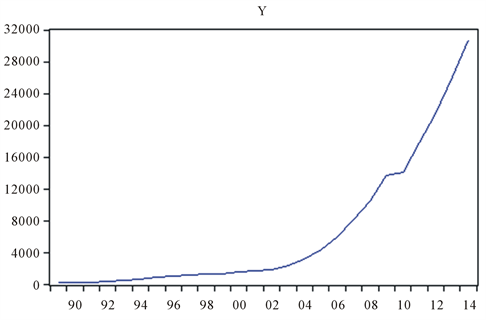
Figure 1. Timing chart of total fixed assets investment in Henan from 1989 to 2014
图1. 中国1989~2014年河南省全社会固定资产投资总额时序图
检验,当计算得到的t统计量的值小于临界值时拒绝原假设(即否定存在单位根) [2] ,ADF检验结果见表1。从表1中,ADF检验中得到的t值为10.55245,大于三个检验水平的临界值,表明该时间序列存在单位根,为非平稳时间序列。非平稳的数据是不能用来建立时间序列模型的,我们需要对数据进行平稳化处理。
2.2. 对数序列的平稳性检验
对于含有指数趋势的时间序列,可以通过对序列取自然对数来消除指数趋势。由于这一序列有着非常明显的指数趋势,因此我们对它进行取自然对数的运算来消除指数趋势的影响,将取对数后的序列命名为
,即
。作出序列的自相关图分别如图2所示。
对
序列作单位根检验,原假设:
;备择假设:
,检验结果如表2所示。
根据这一检验结果,我们看到对原序列取对数以后得序列
依然没有平稳,根据自相关-偏自相关图可以看出,序列中仍有着明显的增长趋势,采用ADF检验方法对序列进行单位根检验,进一步验证序列的非平稳性,检验结果如表2所示,t值为2.866057,大于临界值,接受原假设即
;表明序列
存在单位根,为非平稳序列。根据规律,一阶差分可以消除线性规律,所以需要先对序列
进行差分处理来消除趋势的影响。
2.3. 序列
的差分处理
我们将序列
进行一阶差分处理,得到一个新序列
,即
画出序列
的时序图,并进行相应的单位根检验,如图3、表3所示。
图3为一阶差分后的时序图,从图中可以看出随着时间的推移没有明显的波动变化趋势,初步判断其是一个平稳的时间序列。采用ADF检验方法对序列
进行单位根检验,进一步判断该序列的平稳性,ADF检验结果见表3。从表3可以看出,ADF检验中得到的t值为−3.910395,小于5%及10%显著性水平下的临界值,应当拒绝原假设
;表明该时间序列所有的根在单位圆内,为平稳时间序列。因此,河南省全社会固定资产投资数据是一阶单整序列,记为
。接下来可以针对该序列作进一步的模型拟合。

Table 1. ADF test results of the sequence Y
表1. Y序列的ADF检验结果
表2. ADF检验结果
表3. ADF检验结果
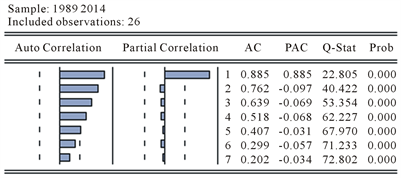
Figure 2. Autocorrelation-partial autocorrelation diagram
图2. 自相关–偏自相关图
3. 模型建立
模型的识别与定阶可以通过样本的自相关与偏自相关函数的观察获得 [3] 。经过平稳性检验,我们建立
,模型经过一阶差分后平稳,所以
,为了获得自回归和移动平均回归中的
和
,可以通过自相关和偏自相关图来观察。图4为
序列的自相关图和偏自相关图。
从图4中可以看出,自相关系数在滞后阶数1、5、6和7时显著不为0,因此
、
、
或者
。偏自相关系数在滞后阶数为1时显著不为0,因此
。为了确定模型的最终结构,需要结合AIC和SC准则定阶,最终来确定模型的阶数。文章建立4个模型,运用Eviews软件根据AIC和SC值来定阶,结果如表4。
从表4中观察到
取(1,5)时,AIC和SIC的值最小。综合比较DW统计量以及
,一般DW统计量越接近2,
越接近1说明模型拟合的越好,最后选定的
模型取(1,1,5)时,模型拟合的较好。为了进一步确定选定的模型是否能够充分的提取数据列的信息,对
进行检验。我们将该模型中的自回归和移动平均中部分不显著的系数放弃,最终的估计结果如图5所示。
模型的具体形式为:
,
,
,
,
,
我们可以推出时间序列
的预测公式为:
进而推出时间序列
的预测公式为:
根据图5中得到的数据:
接近于1,说明模型拟合的很好;DW值接近2,说明不存在自相关关系;AIC和SC值非常小,说明模型拟合的相对合理。
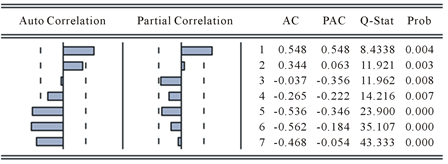
Figure 4. xtautocorrelation-partial autocorrelation of sequences
图4. xt序列的自相关–偏自相关图

Table 4. Comparison of different ARMA ( p , q ) model AIC and SC values
表4. 不同
模型AIC和SC值比较
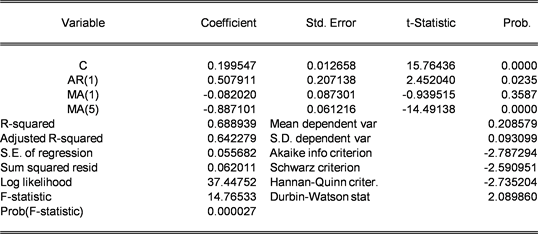
Figure 5. First-order difference model
of the total social investment in fixed assets
图5. 对数全社会固定资产投资总额一阶差分
模型
4. 模型的检验
文章对模型的残差序列进行独立性检验,这里采用拉格朗日乘数检验法(LM检验)对残差序列的样本自相关系数进行检验,原假设是残差序列相互独立。拉格朗日乘数检验的思想是:在约束条件下,可以用拉格朗日方法构造目标函数。如果约束有效,则最大化拉格朗日函数所得估计量应位于最大化无约束所得参数估计值附近。这里也是构造一个LM统计量,该统计量服从卡方分布 [4] 。表5为LM检验结果,可以看出统计量值的p值均大于0.05,应当接受原假设,所以残差序列相互独立,是白噪声序列。
另外从残差序列的自相关图(图6)可以看出,残差序列是纯随机序列,ARIMA(1,1,5)模型的建立较为合理,充分提取了数据中的信息。残差通过了白噪声检验,因而可以判断该模型是可行的,可用于预测分析。
5. 模型的预测
首先进行样本内静态预测,图7为1989~2014年全社会固定资产投资总额预测值与真实值的趋势图,从图中可以看出样本期内河南省社会固定资产投资总额的真实值和预测值两条曲线的拟合情况非常好,走势基本一致,说明模型拟合的很好,非常合理。通过计算样本内各年份河南省全社会固定资产投资的真实值和预测值,1989~2014年内预测的平均误差为2.0%,一般来说预测的误差越小,预测的精度就越高,说明模型拟合的就越合理,由于样本期内预测的平均误差非常小,所以预测的精度非常高,这对于未来几年河南省全社会固定资产投资总额的预测具有重要的参考意义。
为了进一步分析河南省全社会固定资产投资总额,利用建立的ARIMA模型进行样本外动态预测,由于该时间序列模型经过取对数再做一阶差分才基本平稳,且模型数据有限,所以所获得的模型反映的是短期变化关系,而非长期变化关系,因此只对未来四年2015年~2018年的全社会固定资产投资总额进行预测,表6为预测值数据。
从预测的结果来看,未来4年的河南省全社会固定资产投资总额仍将保持较高速度增长,从模型的预测公式我们可以看到,河南省固定资产投资总额与其第一期的滞后值、第五期的随机扰动项密切相关,从参数估计值来看,与第一期的滞后值正相关,与第五期的随机扰动项负相关。因此,政府在引导投资时要考虑到这点。近几年全社会固定资产投资总额与资本形成总额出现严重背离且差额逐渐拉大,目前差额已超过30%,也就是说超过30%的固定资产投资不能形成资本,这值得我们关注和警惕。近几年房地产成为热门,土地交易金在全社会固定资产投资总额中所占比重逐渐提高,到2012年已经超过30%,金额上达
表5. 残差的LM检验结果

Table 6. Estimated total investment in fixed assets of Henan province from 2015 to 2018 (Unit: 100 million Yuan)
表6. 2015年~2018年河南省全社会固定资产投资总额预测值(单位:亿元)
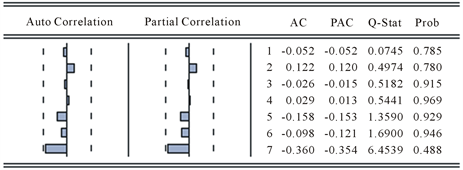
Figure 6. Residual sequence autocorrelation-partial autocorrelation analysis
图6. 残差序列自相关–偏自相关分析图

Figure 7. Real and static estimates of total fixed assets investment in Henan province
图7. 河南省全社会固定资产投资总额的真实值与静态预测值
到12万亿人民币以上,名副其实地出现经济虚拟化、经济地产化,使得全社会固定资产投资总额逐渐大于资本形成总额,两者之间差距越来越大 [5] 。同时经济的虚拟化、经济地产化也是我国近几年用扩大投资的方式拉动经济日益困难,拉动力日益减弱经济增长率降低的一个重要原因 [6] 。我国经济增长的70%以上要靠投资拉动,而投资的30%以上不能对经济增长有所贡献,那么至少降低了20%的经济增长率。如果一个国家或地区固定资产投资有较大增长不能称之为坏事,但是每个地区经济结构不同,总有一些问题会影响自身的均衡发展,制约经济增长。投资过热有时候也会成为自身的累赘,不一定都是好的,要看经济结构能不能承受,所以说,要做到经济结构全面和相对合理是非常困难的。所以政府应当注意:1) 政府应当充分贯彻中央各项宏观经济政策,引导并调整和优化产业投资结构;2) 政府应当合理引导投资比例,提升投资对经济的拉动力,多渠道筹措建设资金,积极争取中央投资和信贷基金支持 [7] ;3) 提高投资收益,大力扶持一些影响力大、有长远发展的投资项目,着力推进产业集聚区建设,积极推进一批重大项目尽快开工建设,切实加快在建项目建设进度,加快保障性安居工程建设,努力实现投资平稳较快增长,为河南省社会发展提供有力支撑 [8] ;4) 坚持把扩大投资需求、调整投资结构作为“转方式、调结构”最直接最有效的方式,激发民众的热情,拓展民间投资领域。
综上所述,ARIMA模型较好的解决了非平稳序列的建模问题,在短期预测方面有着重要的意义。文章借助Eviews软件,将ARIMA模型应用于河南省全社会固定资产投资总额的预测,预测值与真实值非常接近,预测精度较高,说明模型拟合的较好,相对合理,为河南省全社会固定资产投资的制定提供了一个客观和科学的根据。
基金项目
融资租赁与“百城建设提质工程”融资模式研究(河南省政府决策研究招标课题,立项编号:2017B276)。