1. 引言
本文中我们研究的都是有限的、无向的、无环和无重边的图。我们用符号
和
去分别定义图
的顶点集和边集。对于任意的整数
,我们用
去定义整数集
。
路顶点覆盖问题就是去找到最小的顶点集
使得图
中每个长度为
的路都至少包含
中的一个顶点 [1] 。我们定义最小的集合
的基数为
,也被称为图
的
路顶点覆盖数。特别地,我们用长度来表示边数,用次序来表示顶点数。
路顶点覆盖问题的概念是首次由Novotný (2010)和Brešar et al. (2011)在研究无线电安全网络的连通问题上被引入的 [2] [3] 。涂建华在2011年的交通安全控制问题中也提及到
路顶点覆盖问题的概念 [4] [5] 。无线电传感网络的发展起源于军事应用并简记为WSNs。无论如何,WSNs现在多用于一些民用的设施,如环境的监控,家庭自动化装置和交通控制。无线电安全网络系统可以用图论的语言来表示其拓扑结构 [6] ,我们用顶点代表传感装置,用边来描述每对传感装置间传递的信号。我们关注
概括保护方案,它保证每两个无线设备间传输的数据的完整性。我们的方案假设在连通的网络中次序为
的传送路中至少有一个装置被保护 [7] 。本文我们主要研究几类关于圈和路的笛卡尔乘积图的最小的
路顶点覆盖数。
我们首先介绍几个数学符号及定义。对于实数
,我们用
表示不超过
的最大整数,我们用
表示大于
的最小整数。图
和
的笛卡尔乘积图
具有顶点集
,并且当
和
或者
和
时,顶点
和
间有连边。
最后本文内容安排为:第1节为引言;第2节为相关的引理;第3节介绍了
和
的笛卡尔乘积图的最小的
路顶点覆盖数的上界;第4节给出
和
的笛卡尔乘积图的最小的
路顶点覆盖数的下界和推论。
2. 相关的引理
引理2.1 [2] :对于正整数
,
,我们有
引理2.2:根据
路顶点覆盖的定义很显然有如下两个结论:
对于
的简单无向图
而言,
。
如果
是图
的一个子图并且
,那么
。
证明:(1) 假设
是
的一个最小的
路顶点覆盖集,
是
的一个最小的
路顶点覆盖集,显然我们有
,于是
。
(2) 假设
是
的一个
路顶点覆盖集,
是图
的一个子图,那么
是图
的一个
路顶点覆盖集,由于
,于是
。
引理2.3:对于正整数
,
,我们有
。
3.
和
的笛卡尔乘积图的最小的k路顶点覆盖数的上界
在介绍定理3.1之前我们首先给出一个符号
的概念 [8] ,其中
为大于等于3的整数,
是
中小于等于
的最大元素,
是
中大于等于
的最小元素,这样我们称这组数对
为中间
对,很显然
并且使
的和尽可能的小。
定理3.1:如果
,并且
为中间
对,我们有如下的式子
证明:首先我们构造一个最多有
顶点的
路顶点覆盖集去证明不等式的上界。让
并且
.
由于
中未被覆盖的最大连通子图同构于
,于是我们可以很容易得出
是一个
路顶点覆盖集。
在
中我们覆盖了每一个第
个顶点和第
个顶点,由于有
层,所以
。同理,我们有
,由于我们把每个交叉的位置处的顶点算了两次,而且
,所以覆盖集
的大小为
.
同样的,我们也可以通过交换
和
的位置去构造一个有
个顶点的
路顶点覆盖集。这样我们就得到了
的上界。
4.
和
的笛卡尔乘积图的最小的k路顶点覆盖数的下界
定理4.1:对于正整数
,我们有如下结论:
证明:首先在解决不等式下界的时候,我们先给出
的精确值。很容易可以得出
,但是在本定理中我们考虑
。
如果正整数
,我们有
。我们构造一个有4个顶点
路顶点覆盖集
,去证明
。让
,其中
。如果我们删去
中的点
并且删去它的关联边,于是我们得到了
中最大的未被覆盖的子图
并且
。于是
是
的
路顶点覆盖集,因此
。
很显然
,由引理我们得到
。通过
的结构我们知道,我们至少需要一个顶点去覆盖每一个
层中的
路,无论这两层的顶点是否相连我们都定义它们为
,我们可以知道
,因此
。这样我们的等式
得到了证明。
下面我们基于上述面我们证明过的等式给出
的下界,我们可以把
分解成
个同构于
的不交子图,一个圈
(如图1所示),其中
和一个对于奇数来说的
。我们需要至少
个顶点去覆盖每一个同构于
的子图,需要至少
和
个顶点去分别覆盖子图
和
。因此对于奇数
言,
.
对于偶数
而言,我们把
分解成
个同构于
的不交子图和一个次序为
的圈
,其中
,
。我们需要至少
个顶点去覆盖每一个同构于
的子图,需要至少
个顶点去覆盖子图
。因此有
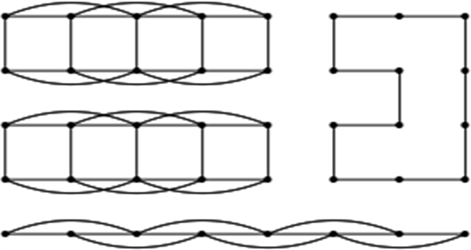
Figure 1. A partition of
for odd m
图1. 当m为奇数时,
的一个分解
.
.
证明:根据定理4.1的证明过程,我们可以把
分解成
个同构于
的不交子图和一个次序为
的圈
,其中
,
。我们需要至少
个顶点去覆盖每一个同构于
的子图,需要至少
个顶点去覆盖子图
。因此有

