1. 引言
液压系统由于具有功率质量比大、运行平稳、快速性好和便于实现自动化等优点,使其在船舶传动与控制领域得到了广泛应用。但由于船舶液压系统工作环境恶劣、单元层次复杂、工况模式多样,再加上液压系统本身固有的密闭性和元器件的复杂性,致使船舶液压系统故障特征不易提取,故障模式很难诊断,严重影响了船舶液压系统运行可靠性,乃至整个船舶装备的航行安全 [1] 。
目前,对液压系统运行状态的监测及故障诊断主要是通过对液压设备及其元器件安装嵌入式传感器来获取系统热力学参数,从而对其运行状态和故障进行评估诊断,这种监测方式具有外界干扰少、诊断范围广、可用性强等特点,目前在液压系统故障诊断领域已有一定范围的应用。但对船舶液压系统这种大型液压设备来说,基于热力学参数的故障诊断方法在工程应用过程中存在下面两个个问题:一是热力参数一般只能进行某些子系统有限故障的监测诊断,对船舶这种关联性强、集成度高的液压系统来说具有一定的局限性;二是船舶液压系统中多数设备或元器件都未设置、预留传感器安装空间,给热力学参数的提取带来了很大的不便。
振动是机械设备运行过程中广泛存在的现象,振动分析法就是利用机械设备在工作时产生的振动信号,经测试分析、数据处理,对内部零部件状态进行诊断的方法。该方法具有诊断速度快,准确率高和能够实现在线诊断等特点,同基于热力学参数诊断法比较,它能较好地克服故障监测范围小、传感器安装空间缺乏等问题,因此在船舶液压系统状态监测与故障诊断领域有着较大的应用空间。但由于船舶本身具有振动信号源多、信号传递复杂等特点,致使其信号呈现明显的非线性,这给振动信号的分析及处理带来了很大的困难 [2] 。
2. EMD技术基本原理
EMD技术从本质上讲是对一个信号进行平稳化处理,其结果是将信号中存在的不同尺度下的波动或变化趋势逐级分解开来,产生一系列具有不同特征尺度的数据序列,每个序列称为一个特征模态函数(IMF) [3] 。对于一个非平稳的信号来说,直接进行希尔伯特变换(HT)得到的结果很大程度上失去了原有的物理意义。而经过EMD得到的各阶段IMF分量都是平稳的,由于EMD都是从信号本身的特征时间尺度出发对信号进行分解,没有固定的先验基底,是自适应的,因此得到的IMF分量一般都具有明显的物理意义,表现了信号内含有的真实物理过程 [4] 。EMD技术同傅里叶变换法相比,其消除了为反映信号的非平稳性而引入的多余且无物理意义的简谐波,使信号分析更加灵活方便;同小波变换相比,EMD技术吸取了小波变换多分辨的优势,却避免了基函数的选择问题。此外,EMD以及与之相关的HT的优点还在于它能客观地处理非线性问题,在非线性结构下,其能够准确地通过波内调制机制反映出系统的非线性,这是以往各种信号处理方法所不能比拟的 [5] 。
对数据信号进行EMD分解就是为了获得本征模函数IMF,然后再对各本征模函数进行希尔伯特变换,得到希尔伯特谱。一个本征模函数必须满足以下两个条件:一是整个时间历程内,穿越零点的次数与极值点数相等或至多相差1;二是信号上任意一点,由局部极大值定义的上包络线和由局部极小值定义的下包络线的均值为0,即信号关于时间轴局部对称 [6] 。第一个条件是很明显的,它与传统的平稳高斯信号的窄带要求类似。对于第二个条件,是一个新的概念,它把经典的全局性要求修改为局部性要求,使瞬时频率不再受不对称波形所形成的不必要的波动所影响。实际上,这个条件应为“数据的局部均值是零”。但是对于非平稳数据来说,计算局部均值涉及到“局部时间尺度”的概念,而这是很难定义的。因此,在第二个条件中使用了局部极大值包络和局部极小值包络的平均为零来代替,使信号的波形局部对称 [7] 。研究表明,在一般情况下,使用这种代替,瞬时频率还是符合所研究系统的物理意义。本征模函数表征了数据的内在的振动模式。由本征模函数的定义可知,由过零点所定义的本征模函数的每一个振动周期,只有一个振动模式,没有其他复杂的奇波;一个本征模函数没有约束为是一个窄带信号,并且可以是频率和幅值的调制,还可以是非稳态的;单由频率或单由幅值调制的信号也可成为本征模函数 [8] 。
经验模态分解后所形成的IMF反映了信号内部固有的波动性,在它的每一个周期上,仅仅包含一个波动模态,不存在多个波动模态混叠的现象,与其他信号处理方法相比,EMD直观、直接、自适应性强,而且具有后验性 [9] 。
3. 模型的构建
3.1. 信号分解模型
由于大多数所有要分析的数据都不是本征模函数,在任意时间点上,数据可能包含多个波动模式,这就是简单的希尔伯特变换不能完全表征一般数据的频率特性的原因。于是需要对原数据进行EMD分解来获得本征模函数。EMD方法分解信号基于以下3个假设:一是信号具有至少两个极值点,即一个极大值点和一个极小值点;二是特征时间尺度定义为相邻极值点之间的时间间隔;三是如果信号没有极值点而仅有拐点,那么在对其分解之前首先将其微分一次或者多次以获得极值点,然后对所得结果进行积分就可得到相应的分量 [10] 。EMD是通过一种被称为“筛分”处理的过程实现对信号的分解,具体过程如下:
(1) 对任一给定信号
,首先确定出
上所有极值点,用三次样条曲线连接所有极大值点形成上包络线,连接所有极小值点形成下包络线。数据
与上下包络线的均值
的差记为
,则:
(1)
将
视作新的
,重复上述步骤,直到
满足IMF的两个条件时,则其称为从原始信号筛选出的第一阶IMF,记为
。通常第一阶IMF分量
包含信号最高频成分。
(2) 将
从
中分离出来,得到一个去掉高频分量的差值信号
,有:
(2)
把
作为新信号,重复(1)的筛分步骤,直到第n阶的残余信号成为单调函数,不能再筛分出IMF分量。
(3)
(3) 数学上,
可表示为n个IMF分量和一个残余项的和,即:
(4)
式中,
为残余量,代表信号中的平均趋势;各IMF分量
则分别代表信号从高到低不同频率段的成分,每一频率段所含的频率成分是不同的,同一IMF分量中,不同时刻处的瞬时频率也是不同,这种不同频率成分的局部时间分布是随信号本身的变化而变化的 [11] 。
3.2. 特征提取模型
EMD方法基于信号的局部特征时间尺度,将信号自适应地分解为若干IMF分量之和,这样使得瞬时频率这一概念具有了实际的物理意义,从而可以计算每个IMF分量的瞬时频率和瞬时幅值 [12] ,对式(1)中的每个特征模态函数
做希尔伯特变换,得到:
(5)
构造解析信号:
(6)
于是得到幅值函数为:
(7)
瞬时频率为:
(8)
为实现对船舶液压系统振动信号特征向量的提取,定义分解后各模态的平均能量为:
(9)
其中,N为每个模态的数据点数。
分解后各层的总平均能量为:
(10)
量归一化各层所占的能量比为:
(11)
3.3. 故障诊断模型
由于系统的振动信号反映了系统的运行状态及故障模式,因此基于系统振动信号提取的特征向量与系统的运行状态及故障模式具有一致性。RBF神经网络无论在逼近能力、分类能力,还是在学习速度方面都有较大优势 [13] ,因此选用方法用于诊断船舶液压系统故障。
RBF网络的结构与多层前向网络类似,它是一种三层前向网络,即包括输入层、隐含层和输出层。其中输入层由信号源节点组成;隐含层由“函数基”构成,用来实现数据源到隐层空间的非线性变换;输出层是线性的,通过组合隐含层上的各维分量,实现对输入向量的响应。该模型的数学表达式为:
(12)
其中,输入向量
,
,
为径向基函数,
为第
个节点的输出权值,输出权值向量
,
。在本模型中,输入向量为处理后的各模态的能力,输出即为液压系统状态和故障模式。
模型中基函数设为高斯函数:
(13)
其中,
为高斯函数的中心,这里指基函数的第
个聚类中心,
为高斯函数的方差。
网络模型构建好后,为获得网络参数的各项配置,应选择液压系统的典型工况对模型进行训练,最后实现对系统故障的精确诊断。
4. 模型验证与分析
为验证EMD技术及RBF诊断模型在船舶液压系统故障诊断领域的可行性,我们以某型船艇装备液压舵机作为对象进行了试验验证。试验以该型舵机的实际故障信息及振动信号为基础,通过EMD分解出IMF分量共8个(含残余分量),对各IMF分量提取特征向量后,以其特征向量为输入,故障模式及系统运行状态为输出实现对RBF网络模型的训练,最后以未训练的同类故障模式的数据为输入,对诊断模型的输出进行了验证。
该型舵机的主要故障模式是舵速慢,而该型船艇装备的转舵速度主要取决于撞杆移动的速度,即供入转舵机构液压缸的油量。供油量大,舵速快;反之,舵速慢。经统计分析,造成该故障模式的原因主要有3个,一是电路故障,致使电压不稳,泵转速变化;二是吸入滤器堵塞;三是油缸内漏 [14] 。
4.1. 信号的分解
将上述三种故障原因及舵机正常工作模式的振动信号各抽出一组分别进行经验模态分解,结果分别如图1所示。
4.2. 特征向量的提取
对分解后的IMF分量进行希尔伯特变换、归一化处理后,得到各分量的瞬时频率和能量比分别如表1、表2、表3、表4所示。
通过对该舵机三种故障模式及其在正常状态下的振动信号进行多组数据分析后,发现其IMF分量的能量占比对不同运行状态呈现不同的分布,基本情况如表5所示。
当舵机处于正常状态时,IMF1分量的能力占比及其他分量能量占比与滤器堵塞故障有重合,但两者在IMF2分量的能量占比方面界限明显;对泵转速波动来说,IMF1分量能量占比较其他状态明显要大,且IMF1分量能量占比与其他分量能量占比基本相当;油缸内漏时,IMF1分量能量占比较其他状态明显要小,且IMF2分量能量占比明显大于其他分量能量占比。
 (a)
(a)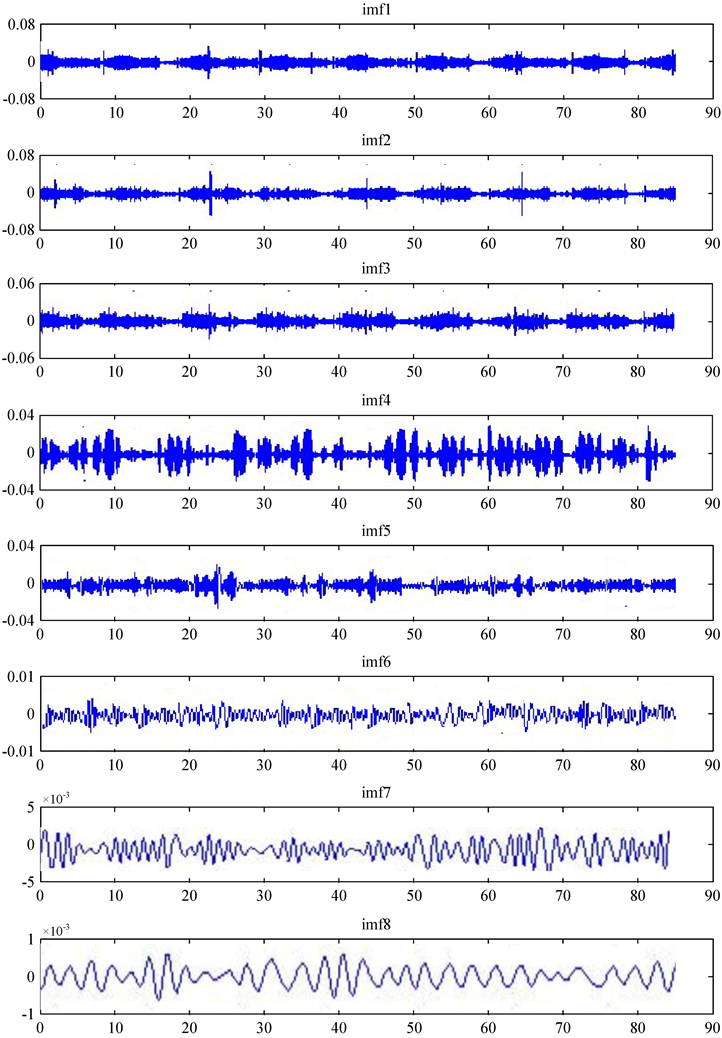 (b)
(b)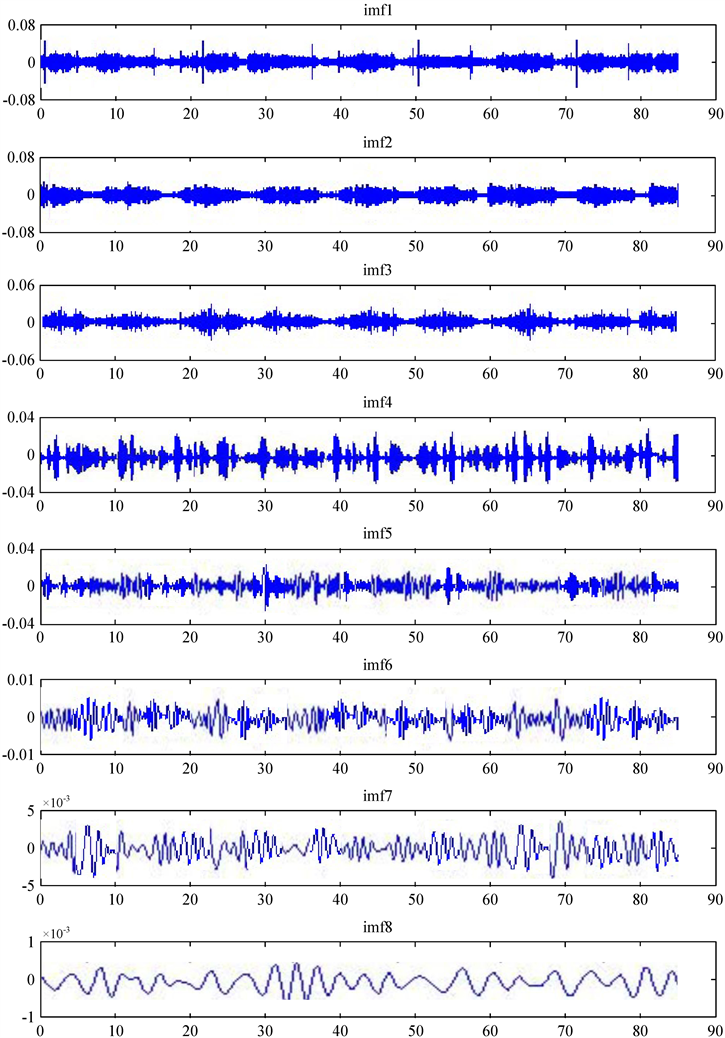 (c)
(c) (d)
(d)
Figure 1. EMD waveform diagram of a steering engine typical fault mode; (a) Normal signal; (b) Pump speed fluctuation signal; (c) Clogged filter signal; (d) Cylinder leakage signal
图1. 某舵机典型故障模式EMD分解分量波形图;(a) 正常信号;(b) 泵转速波动信号;(c) 滤器堵塞信号;(d) 油缸内漏信号

Table 1. IMF component instantaneous frequency and energy ratio of normal signal
表1. 正常信号IMF分量瞬时频率和能量占比

Table 2. IMF component instantaneous frequency and energy ratio of pump speed fluctuation
表2. 泵转速波动IMF分量瞬时频率和能量占比

Table 3. IMF component instantaneous frequency and energy ratio of clogged filter
表3. 滤器堵塞IMF分量瞬时频率和能量占比

Table 4. IMF component instantaneous frequency and energy ratio of cylinder leakage
表4. 油缸内漏IMF分量瞬时频率和能量占比

Table 5. Energy share distribution of IMF components in different states of steering gear
表5. 舵机不同状态下各IMF分量的能量占比分布
4.3. 模型的训练与验证
由于该型舵机在不同状态下,不同IMF分量的能量占比分布不同,根据这一特点,针对上述状态,各选取50组特征向量对诊断网络模型进行训练。
网络模型训练完成后,针对上述4种不同状态,各随机选取5组数据进行验证,验证结果如表6所示。
由表6可以看出,仿真结果与目标向量基本一致。
5. 结束语
EMD作为一种新的信号处理方法目前在信号去噪、非线性振动分析、趋势项提取等方面有着广泛的

Table 6. Comparison table of target vectors and simulation vectors
表6. 目标向量与仿真向量比较表
应用。在机械故障诊断领域,EMD技术还处于方兴未艾阶段,其与小波、支持向量机、神经网络等的综合运用也是当前机械故障诊断领域的一个发展方向。基于EMD技术与RBF网络相结合的船舶液压系统诊断技术既可实现对船舶液压系统故障的精确诊断,也可为其它类似机械设备的故障诊断提供技术参考。