1. 引言
鼓形齿是一种齿形修行方法,能够补偿载荷作用下的齿轮的各种弹性变形量和齿轮的制造误差。这种弹性变形主要是稳定载荷作用下小齿轮的扭转变形和齿轮轴的弯曲变形。鼓形齿是应用较早的一种齿轮修形工艺,但是至今在设计和应用上并未达到完善、合理以及统一。
2. 鼓形齿的鼓形设计
鼓形齿 [1] 的鼓形设计,是按照一定的规律去研究齿轮在齿宽方向的齿形。
目前关于鼓形齿的设计仅仅是给出鼓形量的要求,有的仅仅就是有设计图纸但是并没有齿形轨迹方程,这样的绘图在加工上和控制生产质量方面很难做到统一。
本文鼓形就是在这种仅仅给出加工图纸无法找到准确鼓形轨迹的情况下利用理论计算来分析鼓形轨迹。其中容易发现问题与控制产品质量的方案是按照等半径圆弧来设计,设计方式如图1所示。
(1)
因为鼓形量的单位是μm,且一般都很小,这里一般将
省略,则由式(1)变形得:
.(2)
同理可得任一点的鼓形半径:
. (3)
因为此鼓形设计为等半径设计,所以由式(2)、(3)得任意一点的鼓形量为:
. (4)
利用式(3)对实验数据如图2进行检验,验证这种鼓形齿是否是按照等半径圆弧进行设计的,验算过程如下:
如图2所示,三角形偏转最大值为:
利用相似三角形的知识,可以求出对应各点的公差值(命名规则依据图2图标号取其下标进行区分):

Figure 1. Design of equal radius drum-shaped gear
图1. 等半径圆弧设计的鼓形齿
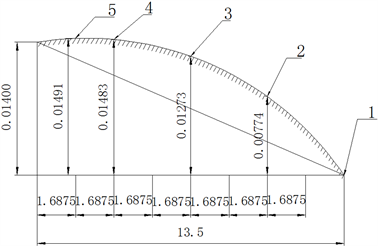

Figure 2. Analysis of the test data processing drum
图2. 试验加工鼓形数据分析
利用图2(a)所示总鼓形量分别对应减去上述所得各值,得到:
每点所对应的鼓形半径为:
相对误差计算如下:
3. ANSYS应力仿真来验证
由计算结果可以看出,最大相对误差只有4.75%,基本可以判定该Gleason机床加工的鼓形是以等半径形式进行加工的,此鼓形是由等半径圆弧进行设计的。
为了ANSYS软件进行齿轮接触应力 [2] [3] [4] [5] 仿真验证方便,选定两齿轮材料相同(均为结构钢),弹性模E1= E2= 2 × 1011Pa,泊松比u1= u2= 0.3,屈服极限σ = 2.5 × 108Pa
图3为标准渐开线齿轮应力分布图,齿轮齿数分别取41与55,齿轮模数均为1.64,其中齿轮1齿宽为15 mm做固定处理,齿轮2齿宽为16.5 mm,施加55 N·m的转矩(其余对比组实验均采用此参数),ANSYS静力学接触应力分析结果表明齿轮接触存在应力集中现象,最大应力为363.1 MPa。
对齿轮进行鼓形加工,依据前面所得的等半径加工方式,依据图4可以得到接触应力相对于正常渐开线齿轮副已经有了明显改善,由363.1 MPa减少为214.45 MPa,并且齿轮表面应力分布较均匀(图5),至于齿面端点处的应力集中现象主要是由于该齿轮未做倒角处理,若端部不接触则不存在应力集中现象,可见鼓形齿设计能够明显改善齿轮的接触应力。主要理论依据是:齿轮受力发生弹性变形,当进行鼓形加工能够依靠齿轮弹性变形将齿轮点受力转变为齿轮面受力,大大减少了齿轮的应力集中。

Figure 3. Stress envelope of standard involute gear
图3. 标准渐开线齿轮应力分布图

Figure 4. Stress distribution of machined the drum shaped gear
图4. 鼓形加工后齿轮应力分布图

Figure 5. Stress of single gear tooth drum after processing distribution
图5. 鼓形加工后齿轮单个齿面应力分布图
4. 结束语
通过理论计算与实际产品进行对比,能够知道鼓形按照等半径进行设计的,这样在加工过程中更容易控制产品质量,保证产品加工精度与技术要求,同时鼓形量能够减少齿轮的接触应力,值得大力推广。
基金项目
山东省科技发展计划项目(13zz15);烟台市科技发展计划项目(2015GX019)。