1. 引言
格子Boltzmann方法(LBM)起源于格子气自动机(LGA) [1] ,并逐渐发展成为计算流体力学的重要数值模拟方法 [2] [3] [4] 。目前,LBM已广泛用于模拟单组分水动力学问题 [2] ,多相和多组分流动,包括悬浮粒子流 [5] ,磁流体 [6] ,多孔介质流 [7] 以及反应扩散系统 [8] 等。此外,LBM在求解非线性物理方程领域也有出色的表现,如波动方程 [9] 、KDV方程 [10] 、Burgers方程 [11] [12] 、非线性Schrödinger方程 [13] [14] [15] 和Poisson方程 [16] [17] 等。本文使用经典的Runge-Kutta公式 [18] 构建了具有高阶精度的格子Runge-Kutta-Boltzmann模型。通过Chapmann-Enskog展开和多尺度展开技术,获得了不同时间尺度的系列偏微分方程和修正的反应扩散方程。数值结果表明,本文所提出的模型可以用来模拟反应扩散方程。
2. 格子Runge-Kutta-Boltzmann模型
2.1. 不同时间尺度的系列偏微分方程
将一个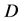 维空间离散成网格,网格中心与相邻的
维空间离散成网格,网格中心与相邻的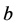 个格点连线作为速度矢量,加上网格中心的静止速度,这样就得到一个
个格点连线作为速度矢量,加上网格中心的静止速度,这样就得到一个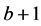 速度模型。定义
速度模型。定义 时刻,
时刻,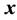 位置的分布函数为
位置的分布函数为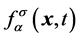 ,用来表示粒子的密度;定义该时刻该位置的速度为
,用来表示粒子的密度;定义该时刻该位置的速度为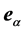 。则标准格子Boltzmann模型演化方程为
。则标准格子Boltzmann模型演化方程为
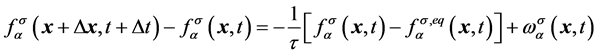 , (1)
, (1)
在方程(1)中,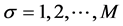 表示组分数;
表示组分数; 为附加项。为得到可以应用于稳态的宏观量,假设存在平衡态分布函数
为附加项。为得到可以应用于稳态的宏观量,假设存在平衡态分布函数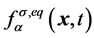 ,并且满足守恒条件
,并且满足守恒条件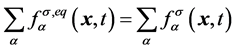 。
。
粒子状态的演化可以分为两步:流动,粒子沿速度方向运动到相邻格点;碰撞,不同速度的粒子发生碰撞并改变速度。所以,方程(1)也可以表示为
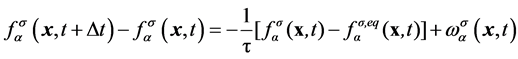 , (
2a
)
, (
2a
)
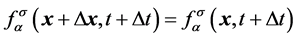 。 (2b)
。 (2b)
引入Knudsen数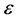 ,选择
,选择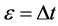 ,
,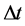 为时间步长 [9] ,将四阶Runge-Kutta公式 [18] 带入方程(
2a
),得到格子Runge-Kutta-Boltzmann方程
为时间步长 [9] ,将四阶Runge-Kutta公式 [18] 带入方程(
2a
),得到格子Runge-Kutta-Boltzmann方程
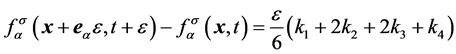 , (
3a
)
, (
3a
)
 ,(3b)
,(3b)
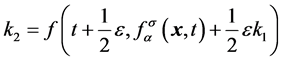 , (
3c
)
, (
3c
)
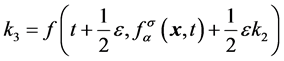 , (3d)
, (3d)
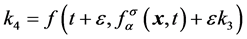 , (3e)
, (3e)
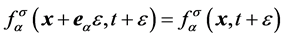 。 (
3f
)
。 (
3f
)
其中, 。
。
对(
3a
)式进行Taylor展开,并保留到 ,得
,得
 , (4)
, (4)
其中,偏微分算子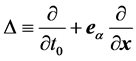 。
。
在小Knudsen数假设下,对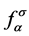 进行Chapman-Enskog展开 [19]
进行Chapman-Enskog展开 [19]
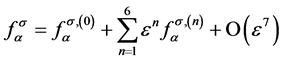 , (5)
, (5)
其中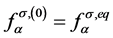 。
。
引入不同的时间尺度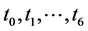 ,其中
,其中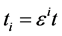 ,
,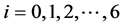 并且满足
并且满足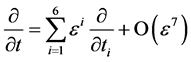 。
。
假设反应和扩散的影响为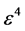 ,即
,即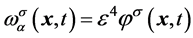 ,求得不同时间尺度的格子Runge-Kutta-Boltzmann模型的系列方程为
,求得不同时间尺度的格子Runge-Kutta-Boltzmann模型的系列方程为
 , (6)
, (6)
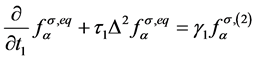 , (7)
, (7)
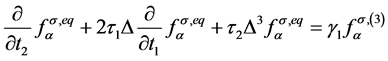 , (8)
, (8)
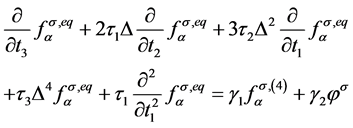 , (9)
, (9)
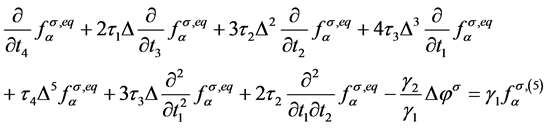 , (10)
, (10)
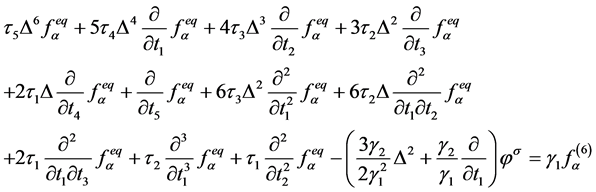 。(11)
。(11)
方程(6)~(11)中,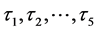 是Chapmann多项式,用来表示修正的反应扩散方程中耗散项和色散项系数,
是Chapmann多项式,用来表示修正的反应扩散方程中耗散项和色散项系数,
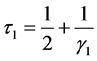 , (12)
, (12)
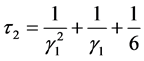 , (13)
, (13)
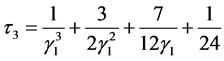 , (14)
, (14)
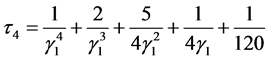 , (15)
, (15)
 , (16)
, (16)
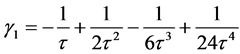 , (17)
, (17)
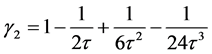 。 (18)
。 (18)
2.2. 反应扩散方程
含源项的一维反应扩散方程为
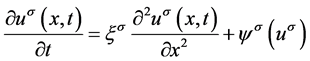 , (19)
, (19)
定义宏观量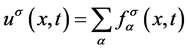 。根据守恒条件有
。根据守恒条件有 。对于反应扩散方程,选取平衡态分布函数的矩为
。对于反应扩散方程,选取平衡态分布函数的矩为
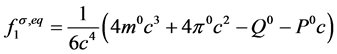 ,(20)
,(20)
 , (21)
, (21)
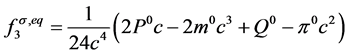 , (22)
, (22)
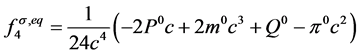 , (23)
, (23)
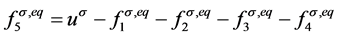 。 (24)
。 (24)
其中 为扩散系数,且
为扩散系数,且 ,
,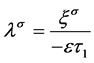 。
。
2.3. 误差分析
将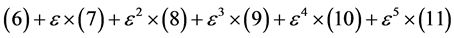 式两端对
式两端对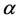 求和,得
求和,得
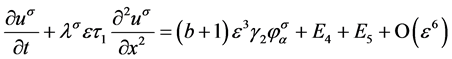 。 (25)
。 (25)
如取方程(19)的源项为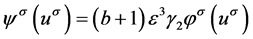 ,则修正后的一维反应扩散方程为
,则修正后的一维反应扩散方程为
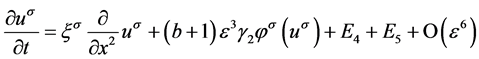 , (26)
, (26)
其中,
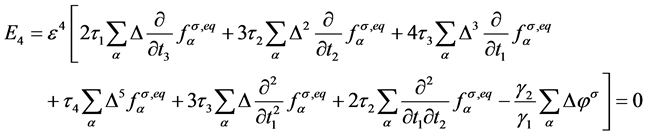 , (27)
, (27)
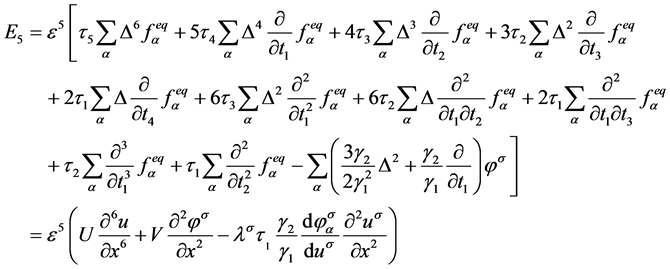 , (28)
, (28)
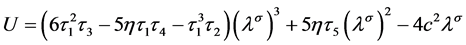 , (29)
, (29)
 。 (30)
。 (30)
方程(28)的主要项为 。根据Hirt启发式稳定性理论,格子Boltzmann模型正耗散条件为
。根据Hirt启发式稳定性理论,格子Boltzmann模型正耗散条件为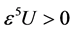 。
。
3. 数值算例
下面应用本文所提出的格子Runge-Kutta-Boltzmann模型求解反应扩散方程。
例1:考虑方程
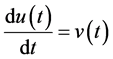 ,
,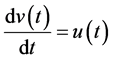 ,
,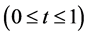 。 (31)
。 (31)
边界条件为
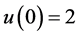 ,
,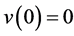 。 (32)
。 (32)
该方程的解析解为
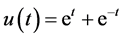 ,
,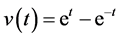 。 (33)
。 (33)
图1和图2给出了数值计算结果。其中图1(a)和图1(b)分别为u-t和v-t的Runge-Kutta算法计算结果、本文的格子Runge-Kutta-Boltzmann模型(在图中表示为LRKB模型)计算结果与解析解的比较;图2(a)和图2(b)分别为u和v的绝对误差曲线,图2(c)为绝对误差E对Knudsen数 的无穷范数曲线。其中
的无穷范数曲线。其中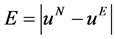 ,
, 为本文的格子Runge-Kutta-Boltzmann模型计算结果,
为本文的格子Runge-Kutta-Boltzmann模型计算结果,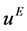 为解析解。其它参数为:
为解析解。其它参数为: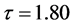 、
、 、
、 、
、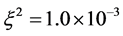 、格子数为51、时间步长为
、格子数为51、时间步长为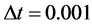 。从图1和图2
。从图1和图2

 (a)(b)
(a)(b)
Figure 1. Comparison between the Runge-Kutta solution, lattice Runge-Kut- ta-Boltzmann solution and the analytical result: (a) u versus t; (b) v versus t
图1. Runge-Kutta模拟结果、格子Runge-Kutta-Boltzmann模拟结果与解析解的比较:(a) u对t图;(b) v对t图


 (a) (b) (c)
(a) (b) (c)
Figure 2. (a) The absolute error of u; (b) The absolute error of v; (c) Curves of the infinite norm of the absolute error E versus the Knudsen number e
图2. (a) u的绝对误差曲线;(b) v的绝对误差曲线;(c) 绝对误差E对Knudsen数e的无穷范数曲线
中可以看出,格子Runge-Kutta-Boltzmann模型模拟结果与解析解有较好的一致性。
例2:考虑反应扩散方程
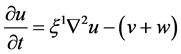 , (34)
, (34)
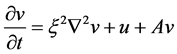 , (35)
, (35)
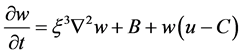 。 (36)
。 (36)
其中,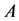 、
、 、
、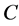 为参数。当
为参数。当 ,
,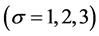 ,方程(34)~(36)简化为Rössler方程 [20]
,方程(34)~(36)简化为Rössler方程 [20]
 , (37)
, (37)
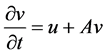 , (38)
, (38)
 。 (39)
。 (39)
在数值模拟中,令方程(26)中附加项为
 。 (40)
。 (40)
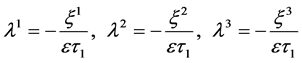 。 (41)
。 (41)
取计算域为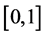 ;初始条件为
;初始条件为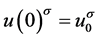 ,
,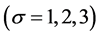 ;边界条件为
;边界条件为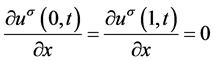 。
。
图3至图5给出了 ,
, 时通过Runge-Kutta算法、文献 [20] 中的格子Boltzmann模型和本文的格子Runge-Kutta-Boltzmann模型绘制的相图。其中图3(a)、图4(a)和图5(a)为使用Runge-Kutta算法得到的v-u、w-u、w-v相图;图3(b)、图4(b)和图5(b)是通过文献 [20] 中的模型计算的v-u、w-u、w-v相图;图3(c)、图4(c)和图5(c)给出了使用本文格子Runge-Kutta-Boltzmann模型绘制的v-u、w-u、w-v相图。其它参数为:
时通过Runge-Kutta算法、文献 [20] 中的格子Boltzmann模型和本文的格子Runge-Kutta-Boltzmann模型绘制的相图。其中图3(a)、图4(a)和图5(a)为使用Runge-Kutta算法得到的v-u、w-u、w-v相图;图3(b)、图4(b)和图5(b)是通过文献 [20] 中的模型计算的v-u、w-u、w-v相图;图3(c)、图4(c)和图5(c)给出了使用本文格子Runge-Kutta-Boltzmann模型绘制的v-u、w-u、w-v相图。其它参数为: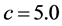 ,
,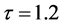 ,
,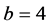 ,
, ,
,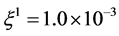 ,
,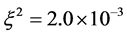 ,
,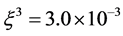 ,格子数为
,格子数为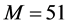 。从图中可以得出,本文模型所得结果与经典四阶Runge-Kutta算法吻合较好,并且比文献 [20] 的结果更精细。
。从图中可以得出,本文模型所得结果与经典四阶Runge-Kutta算法吻合较好,并且比文献 [20] 的结果更精细。


 (a) (b) (c)
(a) (b) (c)
Figure 3. The phase figures of v versus u: (a) the Runge-Kutta formula; (b) the lattice Boltzmann result in Ref. [20] ; (c) the result of the lattice Runge-Kutta-Boltzmann scheme
图3. v对u的相图:(a) Runge-Kutta计算结果;(b) 文献 [20] 模拟结果;(c) 本文格子Runge-Kutta-Boltzmann模拟结果


 (a) (b) (c)
(a) (b) (c)
Figure 4. The phase figures of w versus u: (a) the Runge-Kutta formula; (b) the lattice Boltzmann result in Ref. [20] ; (c) the result of the lattice Runge-Kutta-Boltzmann scheme
图4. w对u的相图:(a) Runge-Kutta计算结果;(b) 文献 [20] 模拟结果;(c) 本文格子Runge-Kutta-Boltzmann模拟结果


 (a) (b) (c)
(a) (b) (c)
Figure 5. The phase figures of w versus v: (a) the Runge-Kutta formula; (b) the lattice Boltzmann result in Ref. [20] ; (c) the result of the lattice Runge-Kutta-Boltzmann scheme
图5. w对v的相图:(a) Runge-Kutta计算结果;(b) 文献 [20] 模拟结果;(c) 本文格子Runge-Kutta-Boltzmann模拟结果
4. 结论
本文使用经典Runge-Kutta算法构建了用于反应扩散方程的格子Runge-Kutta-Boltzmann模型,获得了具有高阶精度的截断误差。数值结果表明,该模型的计算结果与经典Runge-Kutta模型吻合的较好。本文的主要思路,包括不同时间尺度的系列偏微分方程以及平衡态分布函数的形式,可以用来求解其它非线性偏微分方程。
致谢
国家自然科学基金(NO. 51406067,NO. 11272133),吉林省教育厅科研项目(吉教科合字[2016]第141号)资助。