1. 引言
科学、工程技术和金融管理等领域中的许多数据可以用矩阵的形式表示和存储,因此对这些数据的研究与处理往往可以转化为对矩阵的研究与处理。矩阵子直和的概念正是为适应诸如线性补问题,区域分解法中的重叠子域和有限元法中的总刚度矩阵研究的需求而提出和研究的 [1] [2] [3] [4] 。在这些研究中,“某特定矩阵类的子直和是否仍属于该类矩阵”成为研究的重要问题之一。文献 [5] [6] [7] 分别对P-矩阵,Nekrasov矩阵和S-严格对角占优矩阵的子直和进行了研究。本文将对一类重要的特殊矩阵——MB-矩阵的子直和问题进行研究,期望获得MB-矩阵的子直和仍为MB-矩阵的一些充分条件。
2. 预备知识
本节给出一些基本概念、定理与符号,以备后用。
定义2.1 [8] 设 ,如果对于所有的
,如果对于所有的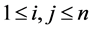 ,
, 都有
都有 ,则
,则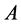 称为Z-矩阵。如果
称为Z-矩阵。如果 是Z-矩阵且
是Z-矩阵且 ,则称
,则称 为M-矩阵。
为M-矩阵。
定义2.2 [5] 设 ,记
,记
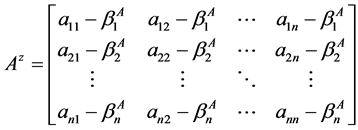 ,
,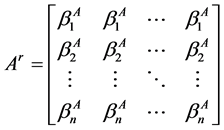 (1)
(1)
其中 。显然
。显然 ,
, 是Z-矩阵,
是Z-矩阵, 是秩1非负矩阵。若
是秩1非负矩阵。若 为M-矩阵,则称
为M-矩阵,则称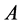 为MB-矩阵。
为MB-矩阵。
定义2.3 [1] 设 ,
,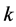 是整数且
是整数且 ,
, ,
, 分块如下:
分块如下:
 ,
, , (2)
, (2)
其中 ,
, 是
是 阶方阵。定义矩阵
阶方阵。定义矩阵
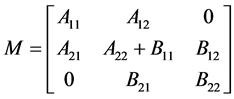 ,(3)
,(3)
为 和
和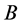 的
的
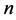 阶k-子直和,记为
阶k-子直和,记为 。
。
设 ,
, 和
和 按定义2.2中的(1)式分别分裂为:
按定义2.2中的(1)式分别分裂为:
 ,
,
 ,
, ,
,
 .
.
记 ,
, ,其中
,其中 ,
, ,
, 。于是有由定义2.3知
。于是有由定义2.3知
 ,
, . (4)
. (4)
其中
 ,
, ,
, ;
;
 .
.
显然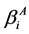 ,
,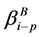 和
和 都是非负的。
都是非负的。
设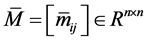 ,其中
,其中
 ,
, .(5)
.(5)
定义2.4 [9] 设 。对任意的
。对任意的 ,记
,记
 ,
, .
.
若
 ,
, ,
,
则称 为(按行)对角(严格对角)占优矩阵;若
为(按行)对角(严格对角)占优矩阵;若
 ,
, ,
,
则称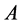 为(按列)对角(严格对角)占优矩阵。
为(按列)对角(严格对角)占优矩阵。
定义2.5 [10] 设 ,若
,若 满足
满足
 ,
,
则称 为严格双对角占优。
为严格双对角占优。
定义2.6 [9] 设 ,若存在正数
,若存在正数 ,使
,使
 ,
,
成立,则称 为广义严格对角占优矩阵。
为广义严格对角占优矩阵。
定义2.7 [9] 设 满足
满足
1) 对角占优,即 ,
, ;
;
2) 非空;
非空;
3) 对每一个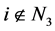 ,存在非零元素序列
,存在非零元素序列 使得
使得 (称之为连接
(称之为连接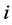 和
和 的非零元素链)。
的非零元素链)。
则称 为具有非零元素链的对角占优矩阵。
为具有非零元素链的对角占优矩阵。
定理2.1 [9] 若 为具有非零元素链的对角占优矩阵,则
为具有非零元素链的对角占优矩阵,则 为广义严格对角占优矩阵。
为广义严格对角占优矩阵。
定义2.8 [9] 设 满足
满足
1) ;
;
2) 。
。
则称 为下半强对角占优矩阵。如果存在置换矩阵
为下半强对角占优矩阵。如果存在置换矩阵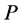 使得矩阵
使得矩阵 为下半强对角占优矩阵,则称
为下半强对角占优矩阵,则称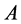 为半强对角占优矩阵。
为半强对角占优矩阵。
定理2.2 [9]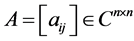 为半强对角占优矩阵的充分必要条件是
为半强对角占优矩阵的充分必要条件是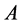 为具有非零元素链的对角占优矩阵。
为具有非零元素链的对角占优矩阵。
推论2.1 [9] 设 为非奇异M-矩阵,
为非奇异M-矩阵,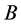 为Z-矩阵且
为Z-矩阵且 ,则
,则 为非奇异M-矩阵。
为非奇异M-矩阵。
定义2.9 [9] 若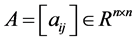 为主对角元为正的Z-矩阵,则称
为主对角元为正的Z-矩阵,则称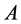 为L-矩阵。
为L-矩阵。
定理2.3 [9] 设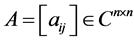 为L-矩阵且为广义的严格对角占优矩阵,则
为L-矩阵且为广义的严格对角占优矩阵,则 为非奇异M-矩阵。
为非奇异M-矩阵。
定理2.4 [5] 设 ,若
,若 为主对角线元为正的严格双对角占优矩阵,则
为主对角线元为正的严格双对角占优矩阵,则 为非奇异M-矩阵。
为非奇异M-矩阵。
定理2.5 [9] 设矩阵 满足
满足
 ,
, ,
, ,
,
并且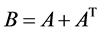 (其中
(其中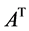 为
为 的转置矩阵)为严格对角占优,则
的转置矩阵)为严格对角占优,则 为非奇异M-矩阵。
为非奇异M-矩阵。
定理2.6 [11] 设 ,则
,则 为非奇异M-矩阵的充要条件是
为非奇异M-矩阵的充要条件是 为Z-矩阵且
为Z-矩阵且 的每一个实特征值为正数。
的每一个实特征值为正数。
定理2.7 [11] 设 ,
, 为
为 的谱,则
的谱,则
 ,
,
其中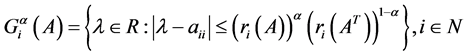 。
。
3. MB-矩阵的k-子直和
首先我们看一个例子。
例3.1 设矩阵 及其按定义2.2的分裂为
及其按定义2.2的分裂为
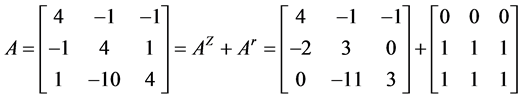 .
.
容易验证上述矩阵为MB-矩阵,由定义2.3得 与
与 的2-子直和
的2-子直和 为:
为:

计算得
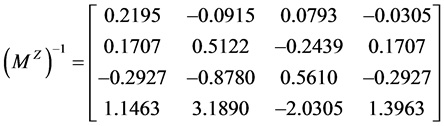 .
.
故 不是M-矩阵.由定义2.1及定义2.2知
不是M-矩阵.由定义2.1及定义2.2知 不是MB-矩阵。
不是MB-矩阵。
例3.1表明MB-矩阵的子直和不一定是MB-矩阵。下面我们讨论MB-矩阵的子直和仍为MB-矩阵的条件。为此,我们先给出如下引理。
引理3.1设 为MB-矩阵,且满足
为MB-矩阵,且满足
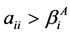 ,
, ;
; ,
, ,
, ,
,
则 为L-矩阵。
为L-矩阵。
证明:因为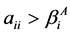 ,
, ,即
,即 ,
, 。由定义2.1知
。由定义2.1知 的主对角元为正,再由(5)式和定义2.9知
的主对角元为正,再由(5)式和定义2.9知 为L-矩阵。
为L-矩阵。
定理3.1设 为MB-矩阵,若
为MB-矩阵,若
1) ,
,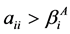 ;
; ,
,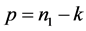 ,
, ;
;
2)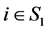 ,
, ;
;
3) ,
, ;
;
4) ,
, 。
。
则 的k-子直和
的k-子直和 为MB-矩阵。
为MB-矩阵。
证明:由条件(1)和引理3.1知 为L-矩阵,由条件(2)-(4)知
为L-矩阵,由条件(2)-(4)知 为严格对角占优矩阵,再由定理2.3得
为严格对角占优矩阵,再由定理2.3得 为M-矩阵。由(4)和(5)式知
为M-矩阵。由(4)和(5)式知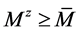 且
且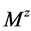 为Z-矩阵,再由推论2.1知
为Z-矩阵,再由推论2.1知 为M-矩阵。从而由定义2.2得
为M-矩阵。从而由定义2.2得 为MB-矩阵。
为MB-矩阵。
引理3.2 设 ,若
,若
1) ,
,
2) 。
。
则 为MB-矩阵。
为MB-矩阵。
证明:由条件(1)知矩阵 是主对角线元为正的Z-阵,由条件(2)知矩阵
是主对角线元为正的Z-阵,由条件(2)知矩阵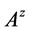 为严格双对角占优矩阵.于是由定理2.4知
为严格双对角占优矩阵.于是由定理2.4知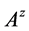 为M-矩阵,再由定义2.2知
为M-矩阵,再由定义2.2知 为MB-矩阵。
为MB-矩阵。
定理3.2 设 为MB-矩阵,满足引理3.1的条件且
为MB-矩阵,满足引理3.1的条件且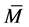 为严格双对角占优矩阵,则
为严格双对角占优矩阵,则 的k-子直和
的k-子直和 为MB-矩阵。
为MB-矩阵。
证明:由引理3.1知矩阵 是主对角线元为正的Z-阵,由
是主对角线元为正的Z-阵,由 为严格双对角占优矩阵知
为严格双对角占优矩阵知

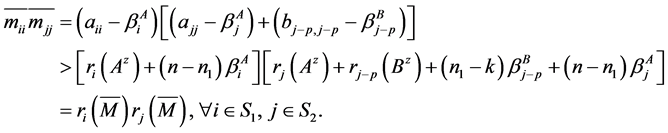

再由(4)式和(5)式知 与
与 的元素在
的元素在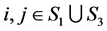 部分的元素是相同的,则当
部分的元素是相同的,则当 时
时 也满足
也满足


下面证明当 时,有
时,有 成立.由于当
成立.由于当 时
时
 ,
,
 ,
,
 ,
,

其中 ,故
,故
 ,
, ,
,
即

从而可以得出
 .
.
类似可得 ,及
,及 的情况同样成立.综上可得
的情况同样成立.综上可得 为主对角元为正的严格双对角占优矩阵,于是由定理2.4知
为主对角元为正的严格双对角占优矩阵,于是由定理2.4知 为M-矩阵,再由定义2.2知
为M-矩阵,再由定义2.2知 为MB-矩阵。
为MB-矩阵。
定理3.3设 为MB-矩阵,若
为MB-矩阵,若
1) ,
, ;
; ,
, ,
,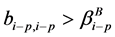 ;
;
2)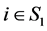 ,
, ;
;
3) ,
, ;
;
4) ,
,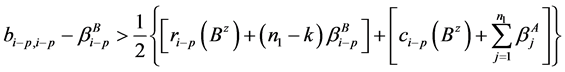 ;
;
则 的k-子直和
的k-子直和 为MB-矩阵。
为MB-矩阵。
证明:由条件(1-4)及定义2.5知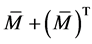 为严格对角占优矩阵,由引理3.1及定理2.5知
为严格对角占优矩阵,由引理3.1及定理2.5知 为M-矩阵。再由(4)和(5)式知
为M-矩阵。再由(4)和(5)式知 且
且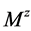 为Z-矩阵。于是由推论2.1知
为Z-矩阵。于是由推论2.1知 为M-矩阵。从而由定义2.2得
为M-矩阵。从而由定义2.2得 为MB-矩阵。
为MB-矩阵。
定理3.4设 为MB-矩阵,若
为MB-矩阵,若
1)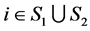 ,
, ;
; ,
, ,
, ;
;
2) ,
, ;
;
3) ,
, ;
;
4) ,
, 。
。
则 的k-子直和
的k-子直和 为MB-矩阵。
为MB-矩阵。
证明:由条件(1)知 为L-矩阵,故
为L-矩阵,故 的主对角元
的主对角元 为正。设
为正。设 为
为 的实特征值,由定理2.7知,存在
的实特征值,由定理2.7知,存在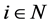 ,使得
,使得
 ,
,
即
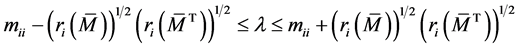 .
.
于是由条件(2)知,当 时,
时,
 .
.
由条件(3)知,当 时,
时,
 .
.
由条件(4)知,当 时,
时,
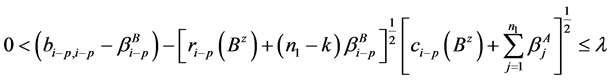 .
.
综上知 的实特征值
的实特征值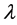 为正,由定理2.6得
为正,由定理2.6得 为M-矩阵。由(4)和(5)式知
为M-矩阵。由(4)和(5)式知 ,又由推论2.1得
,又由推论2.1得 为M-矩阵,再由定义2.2得
为M-矩阵,再由定义2.2得 的k-子直和
的k-子直和 为MB-矩阵。
为MB-矩阵。
定理3.5 设 为MB-矩阵,若
为MB-矩阵,若
1) ,
, ;
; ,
, ,
, ;
;
2) ,
, ,
,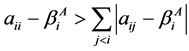 ;
;
3) ,
, ,
,
 ;
;
则 为MB-矩阵。
为MB-矩阵。
证明:由 满足条件(1-3)及
满足条件(1-3)及 与
与 间元素的关系可得
间元素的关系可得 满足:
满足:
当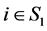 时,
时,
 ,
, ;
;
当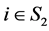 时,
时,
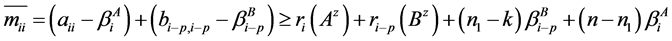 ,
,
 ;
;
当 时,
时,
 ,
,
 .
.
故 为下半强对角占优矩阵.由引理3.1及推论 3.4知
为下半强对角占优矩阵.由引理3.1及推论 3.4知 为非奇异M-矩阵.由(4)和(5)式及推论2.1得
为非奇异M-矩阵.由(4)和(5)式及推论2.1得 为M-矩阵,再由定义2.2知
为M-矩阵,再由定义2.2知 为MB-矩阵。
为MB-矩阵。
下面我们用例子对所获理论结果进行说明。
例3.2设
 ,
, .
.
容易验证 均为MB-矩阵。取
均为MB-矩阵。取 ,由
,由 得
得 ,
, ;
; ,
, ,
, 。考虑
。考虑 的2-子直和
的2-子直和
 .
.
计算可得,当 时
时
 ,
, ,
,
 ,
, ,
,
 ,
,
 ,
, ,
,
 ,
,
 ,
,
 ;
;
 ,
,
 ;
;
当 时
时
 ,
,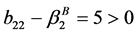 ,
,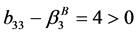 ,
,
 ,
, ,
, ,
,
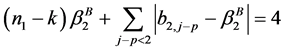 ,
, ,
,
 ,
, ,
, ,
,
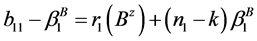 ,
,
 ,
,
 ;
;
 ,
,
 .
.
故矩阵 满足定理3.5的条件(1)-(3),于是由定理3.5知
满足定理3.5的条件(1)-(3),于是由定理3.5知 的2-子直和
的2-子直和 为MB-矩阵。
为MB-矩阵。