1. 引言
公路桥梁上的车辆数量、速度和间距等具有较大随机性，其车桥耦合动力学的研究也较铁路桥梁晚。20世纪90年代以来，这方面研究越来越多，模型也趋于复杂。Huang等 [1] 采用11自由度车辆模型研究了曲线钢箱梁的车桥耦合动力响应。Yoon [2] 等推导出7自由度曲梁单元振动方程，研究了薄壁曲梁的动力特性。Kim [3] 等采用三维有限元方法计算了汽车通过曲线梁桥的动力响应。赵跃宇等 [4] 从4个方面概括了国内外曲线梁的研究现状。黄晓敏 [5] 等则对多车荷载作用下的混凝土曲线箱梁桥冲击效应进行了较详细的分析。
近年来，连续曲线钢箱梁桥在城市高架桥中已得到广泛应用，而既有研究多集中在混凝土梁桥和简支人行桥的动力响应分析。本文采用空间曲梁单元模拟桥梁结构，弹簧阻尼器相连的多刚体系统模拟车辆，建立起车–桥耦合系统动力学模型，并以某连续曲线钢箱梁桥为例，基于自编程序对该耦合系统进行动力响应分析，所得结论可供相关工程应用参考。
2. 车辆–桥梁耦合系统动力响应分析模型
2.1. 桥梁有限元模型
为更好地考虑曲梁杆件翘曲效应的影响，桥梁结构采用图1所示考虑约束扭转的每节点七自由度空间曲梁单元模型 [6] 进行离散，运用弹性系统势能驻值原理和形成矩阵的“对号入座”法则推导出单元的特性矩阵，经坐标变换和组装得到结构的总体质量、阻尼、刚度矩阵，建立起桥梁的动力学方程：
(1)
式中：
分别为结构的总体质量矩阵、阻尼矩阵和刚度矩阵；
、为总体位移、速度和加速度列向量；
为结构的总体外荷载向量。文中桥梁结构的阻尼采用Rayleigh阻尼假设。
2.2. 汽车车辆分析模型
本文车辆模型采用7自由度多刚体系统模型，由一个车体和四个车轮组成。模型考虑了车体及车轮
Figure 1. Beam element considering constraint torsion
图1. 考虑约束扭转影响的梁单元模型
竖向的浮沉运动、车体前后的点头运动、车体横向的倾覆运动，较全面地模拟了车辆自身的振动特性。分析过程中假定车辆平行于桥梁中心线做匀速运动，车辆各构件做小位移振动，每个集中质量的离心力水平作用于各自的质心处。车辆的简化模型见图2，基于势能驻值原理和“对号入座”法则建立车辆的动力学方程如下，详细过程参见文献 [7] 。
(2)
2.3. 路面不平度
诸多文献 [3] [8] 表明路面平顺状况是车–桥动力响应的主要影响因素之一。本文采用文献 [9] 中基于频率功率谱等效的方法，根据国标所给的不平顺谱密度函数 [10] ，对桥面不平度值进行数值模拟，经傅里叶变换为时域样本，以模拟不同等级的路面状况：
(3)
式中：
为时间序列
的频谱，
为虚数单位。
2.4. 车–桥系统动力学方程的建立及求解
基于前述的桥梁和车辆动力方程，以桥梁静力平衡状态为车桥系统的初始状态，即将
代入式(1)，并将桥梁和车辆各矩阵进行组装，由此形成车辆–桥梁耦合系统动力学方程如下，式中各项意义详见文献 [6] ：
(4)
其中：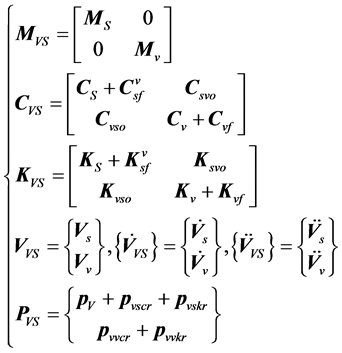
本文采用无条件稳定的Wilson-θ数值积分法求解上述方程 [11] ，为体现出外荷载的变化规律和结构动力响应的周期规律，同时保证计算精度，时间步长取
。据上述原理，本文采用Fortran语言编制了车–桥系统动力分析程序VBDS-1，可方便进行车辆与桥梁的动力响应分析。
3. 工程概况
3.1. 桥梁概况
以某高架线路中跨越道路口的桥梁为例，其跨径布置为
，曲率半径600 m，为全钢结构等高度连续钢箱梁。梁高2.45 m，顶板宽25 m，采用整幅单箱四室的箱型截面如图3，桥面布置为双向六车道。下文中若未加说明，桥面状况取为B级(好)，桥梁阻尼比为1%。根据子空间迭代法，用Fortran编写桥梁自振特性分析程序，求解主梁前N阶自振频率和振型，与ANSYS软件的前5阶自振特性计算值对比如表1，可知两者结果基本吻合。
3.2. 车辆参数
研究采用车队的方式进行加载，以模拟现实中横向多车道且纵向每车道同时有多辆车作用于桥梁的情况。选取每列车队含10辆汽车，前后间距20米，假定后车行驶在前车的车辙上进行分析。根据文献 [7] 选取汽车参数如表2。
4. 车辆荷载作用下桥梁动力响应参数分析
4.1. 桥梁曲率半径的影响
为分析曲率半径的影响，保持该桥跨径等基本参数不变，按车辆以一个车队行驶于外半幅的中心处通过桥梁，偏心距为e = 6 m，分别计算各条件组合下桥梁的位移及内力动力响应如下，限于篇幅只给出了部分结果。
图4可见，桥梁跨中位移和弯矩响应的变化规律基本一致。随着曲率半径的减小，两种响应均有增大趋势，但增速较缓；当曲率半径小于120 m时，其响应最大值将明显增大。
图5可知，支点截面弯矩随曲率半径的变化趋势与跨中相似，但前者在较高车速下出现共振现象，后者则出现在较小车速下；曲率半径越小桥梁跨中截面的扭矩呈增大变化，且半径小于120 m时，扭矩也出现明显增大，其动力放大效应大于弯矩。
4.2. 车辆偏载的影响
分别取车队偏心
三种情况进行分析，计算各车速下桥梁动力响应如图6。可知随着车辆行驶偏心距增大，桥梁跨中位移响应逐渐变大。这是由于车辆偏心的不同使桥梁的扭转效应变大所引起的，可见曲线桥的扭转效应对其动力响应有较大影响，设计时不应忽视。
Table 1. Comparison of bridge natural vibration characteristics
表1. 桥梁自振特性计算结果对比
Table 2. Vehicle parameters of geometry and dynamic
表2. 车辆的几何及动力特性参数
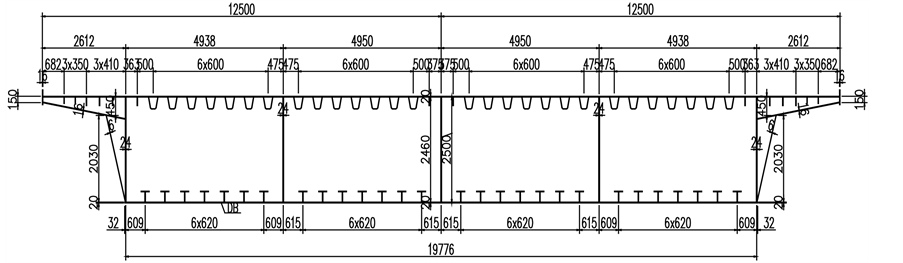
Figure 3. Standard cross section of steel box girder
图3. 钢箱梁标准横截面图(单位：mm)
Figure 4. Displacement and bending moment DMF of midspan in different curve radius
图4. 不同曲率半径下中跨跨中位移和弯矩响应最大值
Figure 5. Maximum of bending moment at supported section and torque at midspan in different curve radius
图5. 不同曲率半径下支点截面负弯矩和跨中截面扭矩最大值
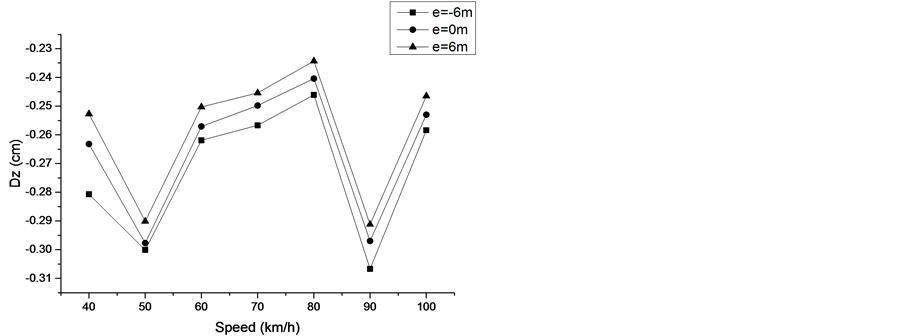
Figure 6. Displacement maximum of midspan in different eccentricities
图6. 不同车辆偏心作用下中跨跨中竖向位移最大值
4.3. 横向加载车道数的影响
分别取单车道偏载(L1)，单向三车道偏载(L3)和双向六车道满载(L6)，车队均沿着桥梁最外沿外侧按照最小间距布置，计算桥梁动力放大系数(DMF)如图7。通常随着横向加载车道数的增多，车辆荷载增大，桥梁的响应也成倍增大，而DMF却相反，图6表明其随车道数的增多而有所减小。
4.4. 纵向车辆行驶间距的影响
参考相关研究 [12] ，选取纵向行车间距10 m，15 m，20 m三种行车间距组成相应的车队，计算桥梁动力响应如图8。可知行车间距增大时，动力放大作用有小幅增大的趋势。值得一提的是，间距从10 m变到20 m，荷载大小增加一倍，而DMF最大变化不超过20%。故间距变化引起车辆数目的增减仍起控制作用，间距增大，DMF虽增大，但桥梁最终的响应值减小。
5. 结论
本文以连续曲线钢箱梁桥为研究对象，建立起车–桥耦合系统进行动力响应分析，主要结论如下：
1) 曲线梁桥的位移和内力响应量值随曲率半径的减小而逐渐增大。当曲率半径小于某定值后，其各
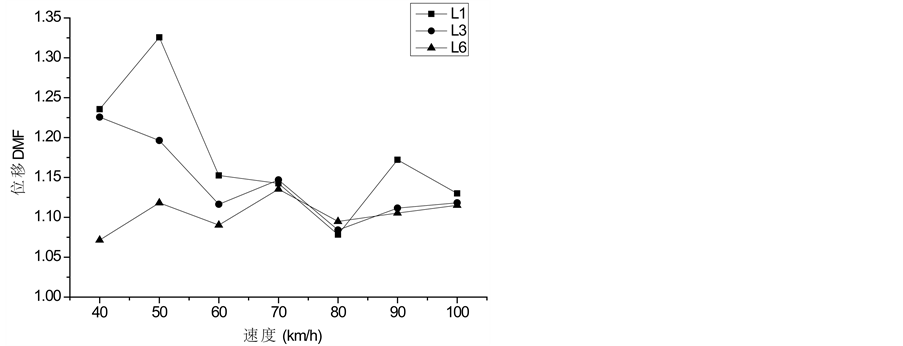
Figure 7. Displacement DMF of midspan in different number of lanes
图7. 不同加载车道数下中跨跨中位移动力放大系数
Figure 8. Displacement DMF of midspan in different vehicle distances
图8. 不同车辆行驶间距下中跨跨中位移动力放大系数
项动力效应将迅速增大；此时扭矩的放大效应要大于弯矩，扭转效应对各项动力响应将产生较大影响；计算时不同车道的偏心作用也不可忽视。
2) 曲线梁桥的动力放大系数随横向加载车道数的减小而增大，随纵向车辆行驶间距的增大而增大，但其并不控制设计，此时车辆数目增减引起响应量值的变化仍起控制作用，实际设计中应综合考虑两者影响。
基金项目
国家自然科学基金资助项目(51378504)。
*通讯作者。