1. 引言
准确可靠的中长期径流预报对防汛抗旱、水库运行调度以及水资源规划管理等有着十分重要的意义 [1] 。中长期径流预报从传统的多元回归分析、逐步回归分析、自回归模型等模型方法到近年的人工神经网络、遗传规划、支持向量机等智能方法，涌现了很多研究成果 [1] - [3] 。其中支持向量机(SVM)是通过核函数实现高维空间的非线性映射 [4] ，能够较好地描述径流的非线性特征，是水文领域近年来的研究热点。最小二乘支持向量机(LSSVM)采用二次规划方法将传统支持向量机中的不等式约束变为等式约束，提高了收敛速度，具有较好的非线性拟合能力 [5] 。然而径流时间序列本身具有典型的非线性和非平稳性特征，SVM和LSSVM模型虽然能够较好地描述径流的非线性特征，但在处理径流的非平稳性上存在缺陷。径流时间序列是被噪声污染的一系列准周期信号的组合 [6] ，对输入序列数据进行预处理可以提高模型的预测精度。奇异谱分析(SSA)，是一种有效的数据预处理技术，广泛应用于径流预报中 [6] - [9] 。因此本文运用SSA对原始序列数据进行预处理，以消除噪声，采用SAR(1)模型、SVM模型和LSSVM模型对水布垭水库1951~2009年的月入库径流原始序列和重建序列进行预测，将数据处理前后的三个模型预测结果进行比较，对比分析数据预处理对模型预测精度的影响。
2. 方法和模型
2.1. 奇异谱分析
奇异谱分析是一种广义的功率谱分析，具有稳定的识别和强化信号功能，其优点在于能够提取蕴含在时间序列中的不规则波动和随机性特征，消除噪声 [10] 。
2.1.1. 建立相空间
SSA的分析对象是一维时间序列，首先将所观测到的一维时间序列
按照给定的嵌套空间维数(即窗口长度)建立相空间轨迹矩阵：
(1)
式中：X称为相空间中的轨迹矩阵；L(1 < L < N)称为窗口长度。
2.1.2. 奇异值分解
类似于常规的经验正交函数(Empirical Orthogonal Function, EOF)分解，轨迹矩阵X也可以进行奇异值分解，令
，可计算出矩阵S的特征值和其所对应的正交特征向量，则矩阵X的分量式为：
(2)
式中：
；
是时间EOF，记为T-EOF，
是时间主分量，记为T-PC，
是
表示的时间型在原序列
时段的权重 [11] 。
2.1.3. 重建成分
SSA最重要的应用功能是通过重建成分(Reconstructed Components, RC)实现的，它在预报中用于提取有用信息，过滤掉噪声 [11] 。
根据最小二乘法建立最优规则，求解重建成分RC，由第K个T-EOF和T-PC重建
的成分记为
，将第k个重建成分用
表示，可以产生L个长度为N的时间序列
，即原始序列被分解为L个子序列的和，如下式所示：
(3)
式中：
。
从序列中选取p(1 ≤ p ≤ L)个具有贡献作用的有用成分进行重建，则p个序列之和等于重建序列，如下式所示：
(4)
该重建序列是被SSA滤去噪声后的有用序列，蕴含原序列的周期成分。
2.2. 季节性一阶自回归模型
月径流由于有以年为周期的变化特点，其序列的统计参数与时间有关，故序列是非平稳的，考虑月径流的这种特性，采用广泛应用的月径流模型，季节性一阶自回归模型，SAR(1)，设
为月径流序列，
表示年份，
表示月份，则模型表达式为：
(5)
式中：
是
年
月的径流量；
和
为第
月的两个回归参数；
是
年
月的独立随机项。参数
和
的计算公式为：
(6)
(7)
式中：
和
分别为第
、
月份的径流量均值；
、
为第
、
月份的径流量标准差；
为第
月的一阶相关系数
(8)
将所求的相关系数及参数代入式(5)中，即可得到预报方程，实现月径流预报。
2.3. 支持向量机模型
给定长度为N的训练集
，其中x为m维输入向量，
是
对应的输出值，支持向量回归的基本思想就是通过一个非线性映射
将数据
映射到高维特征空间F，并在该空间进行线性回归，即
(9)
式中：
为超平面的权值向量，b为偏置项。
根据支持向量机理论，可将线性回归方程转化为优化问题求解，目标函数如下：
(10)
约束条件：
(11)
式中：
，
为松弛变量，
为Vapnik-
不敏感代价函数所定义的误差，常数C > 0，为惩罚函数。
为求解这样一个优化问题，根据Kubn-Tucker条件，引入拉格朗日函数：
(12)
式中：
，
，
，
都为拉格朗日乘子，同时约束条件可转化为：
(13)
因此，非线性回归问题可以通过解式(10)的对偶问题求解：
(14)
求解此式即可得到回归函数：
(15)
其中核函数
是高维特征空间的内积，满足Mercer条件。目前研究最多、最常用的核函数为高斯径向基函数，本文亦采用此函数：
(16)
2.4. 最小二乘支持向量机
最小二乘支持向量机于1999年由Suykens等 [12] 提出，它不仅具有支持向量机泛化能力强、全局最优等优点，并且将支持向量机中求解二次规划问题转化为求解线性方程组问题，因而极大地简化了计算，提高了收敛速度 [4] 。其与支持向量机的不同点是在优化目标中选取了不同的损失函数，最小二乘支持向量机的损失函数选取误差
(允许错分的松弛变量)的二范数。则最小二乘支持向量机根据结构风险最小化准则的优化问题为：
(17)
约束条件为：
(18)
通过引入拉格朗日函数来求解式(17) (18)的优化问题，最优的拉格朗日乘子和b可根据KKT(Karush-Kuhn-Tucker)条件和训练样本集
求得，核函数亦选取高斯径向基函数，具体公式见文献 [4] ，即可得最小二乘支持向量机的回归函数模型。
LSSVM用等式约束代替不等式约束，将支持向量机中求解二次规划问题转化为求解线性方程组问题，降低了计算的复杂性，提高了收敛速度。
3. 实例分析
水布垭水库坝址位于清江流域中游的巴东县水布垭镇，控制面积为10,860 km2，水库正常蓄水位400 m，总库容45.8亿m3，多年平均流量299 m3/s，多年平均径流量为94.4亿m3。采用水布垭水库1951~2009年(共计59年，708个月)的入库月径流资料进行分析研究。
3.1. 数据预处理
3.1.1. 数据标准化
为了消除数值不同量级之间的相互影响，加快模型的识别精度与收敛速度，对资料数据进行标准化处理 [13] 。
(19)
式中：
,
分别表示t时刻的原始值和标准化后的月径流量，
表示月径流量的均值，
表示月径流量的标准差。
3.1.2. SSA参数选择
运用SSA处理数据时，窗口长度L和贡献成分个数P是两个重要的参数。窗口长度的选择直接影响着时间序列的有效分解，决定能否准确捕捉时间序列的结构特征。窗口长度的选取没有一个统一的标准，本文基于检验期不同窗口长度下模型的预测值与实测值的均方误差最小的原则 [8] 来选取窗口长度。考虑到月径流序列存在年周期，具有季节性，故本文在[3,12]之间选取最优窗口长度L。均方误差(Root Mean Square Error, RMSE)的计算式为：
(20)
式中：n是检验期径流量个数，
是检验期第t个时段径流预测值，
是检验期第t个时段径流实测值。表1列出了检验期内三个模型在窗口长度L取[3,12]时的均方误差，结果表明SAR(1)、SVM、LS-SVM三个模型分别在L = 3、L = 11、L = 11时均方误差最小，因此运用奇异谱分析对数据进行预处理时，SAR(1)模型、SVM模型和LS-SVM模型的最优窗口长度分别取3、11和11。
SSA另一个重要的参数是贡献成分的个数P。给定一个窗口长度L后，原始序列被分解为L个子序列，从L个子序列中准确识别贡献成分是提取序列中的有用成分滤去噪声的关键。本文采用互相关函数法 [9] 来确定贡献成分P的个数。分别计算各个窗口长度下L个子序列与原始序列的互相关系数，并将统计结果列于表2。互相关系数为正的序列即为原始序列的贡献成分，而互相关系数为负的序列即为噪声。如从表中知，当L = 3时，子序列2和子序列3为贡献成分，则将两者叠加构成重建序列RC，作为模型的输入。
Table 1. RMSE values of models under various window lengths L during testing periods
表1. 检验期内模型在各个窗口长度下均方误差
Table 2. Cross-correlation function values between subseries and original series under various window lengths L
表2. 各个窗口长度下子序列与原序列的互相关系数
3.1.3. 预报因子的选取
中长期径流预报中，假设未来径流值与过去径流值之间存在某种确定的函数关系，利用过去的观测值估计未来值 [14] ，其数学描述为：
(21)
式中：Q(t)为当前时段月径流量，
为当前时段径流的m个时段前期影响月径流量。
SAR(1)模型是用前一个月的径流预测当前时段的月径流，故预测因子为前一个月的径流。而SVM模型和LSSVM模型的预报因子的个数对训练结果有很大的影响，个数过小，则没有足够的序列信息让模型去捕捉，若个数过大，则会引入过多的噪声，不仅增加模型的训练时长，而且可能会干扰训练结果，因此采用SVM和LSSVM建模时，选择合适的时滞参数m至关重要 [15] 。本文采用自相关函数法 [8] 确定时滞参数m，图1和图2表示了原始径流序列与L = 11时重建序列在滞时为1~24月的自相关函数值。从图1知，原始序列的自相关函数在m = 12时取最大值，而图2中重建序列在m = 1时自相关函数最大，m = 12时次之，然而预报因子越多，所包含的信息越多，且为方便比较，均选取前12个月的径流数据作为SVM和LSSVM模型原始序列和重组序列的预报因子。
3.1.4. 模型的评价指标
基于水文情报预报规范，本文选取以下四个指标作为预测模型的精度评价指标：
(1) 纳什模型效率系数
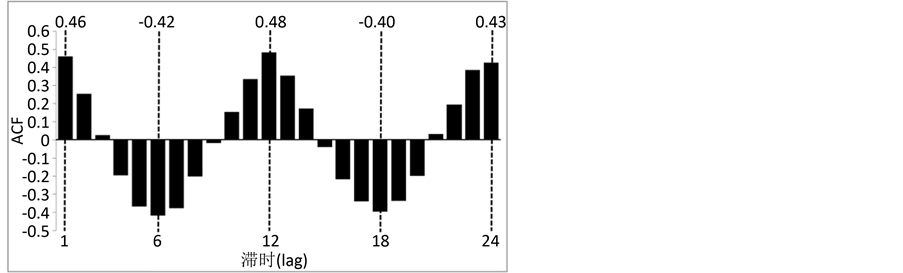
Figure 1. Autocorrelation function of the original series
图1. 原始序列的自相关函数值
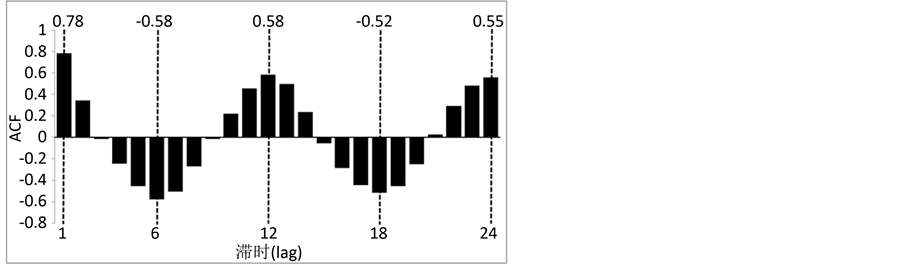
Figure 2. Autocorrelation function of the reconstructed series under L = 11
图2. L = 11重建序列的自相关函数值
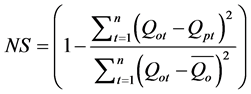
(2) 水量平衡系数
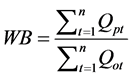
(3) 年均最大径流的相对误差
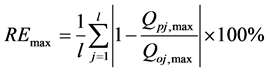
(4) 年均最小径流的相对误差
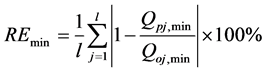
式中：n是径流序列的长度，l是年份数；
和
分别表示t时刻径流的预测值和实测值；
是实测径流均值；
和
分别表示第j年最大径流的预测值和观测值；
和
分别表示第j年最小径流的预测值和观测值。NS和WB越接近于1，表示模型效果越好；REmax和REmin越接近于0，表示模型对极大值和极小值模拟预测能力越好。
3.2.结果分析
本文选取水布垭水库1951~2009年的入库月径流资料进行分析，将1951~1998年的月径流资料作为训练数据，1999~2009年的月径流资料作为检验数据。运用三个模型分别模拟预测原始序列和重建序列，率定期和检验期的模拟预测结果见表3，并在图3~5中绘制了三个模型检验期132个月的预测值与实测值，直观分析模拟预测效果。
3.2.1. SAR(1)模型模拟预测结果
如表3所示，经过奇异谱分析预处理后，SAR(1)模型在训练期的模型效率系数由原来的48%提升到56%，水量平衡系数为100%，且年均最大径流相对误差和年均最小径流相对误差均有所降低，SAR(1)模型在训练期模拟精度虽有一定提升，但模型的检验期在预处理前后，预测精度变化不大，这说明奇异谱分析对SAR(1)模型模拟预测精度的提高影响不大。
3.2.2. SVM模型模拟预测结果
由表3得出，数据预处理前，SVM模型率定期和检验期的纳什效率系数为45%、43%，检验期的年均最大和最小径流相对误差分别高达29%和39%，模型对洪水和枯水期的预测能力不足。经过奇异谱分析对原始数据进行预处理后，模型的精度大幅度提升。SVM模型检验期的纳什效率系数达82%，水量平衡系数也接近于1；
Table 3. Performance results of models during training and testing periods
表3. 率定期和检验期各模型的模拟结果
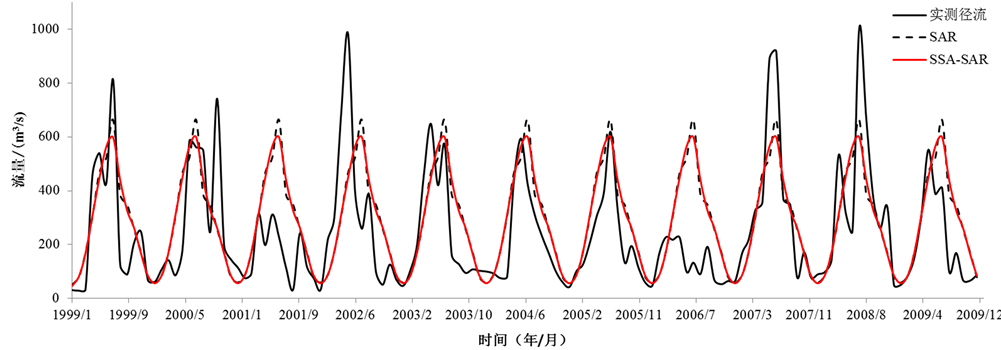
Figure 3. Comparison of observed inflow and predicted inflow by the SAR and SSA-SAR during testing period
图3. 检验期模型SAR和SSA-SAR的预测值与实测值对比图
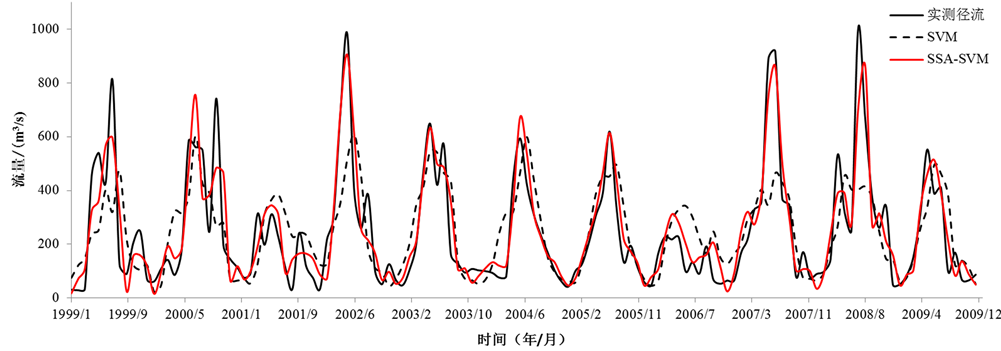
Figure 4. Comparison of observed inflow and predicted inflow by the SVM and SSA-SVM during testing period
图4. 检验期模型SVM和SSA-SVM的预测值与实测值对比图
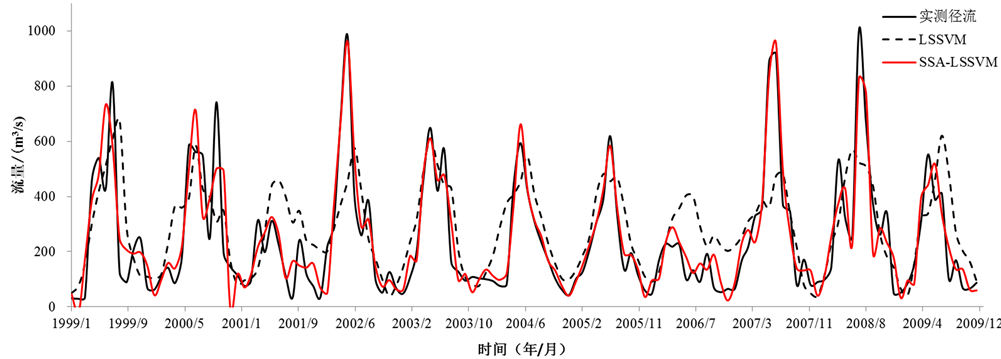
Figure 5. Comparison of observed inflow and predicted inflow by the LS-SVM and SSA-LSSVM during testing period
图5. 检验期模型LSSVM和SSA-LSSVM的预测值与实测值对比图
检验期的年均最大径流相对误差从原有的29%降低到12%，然而年均最小径流相对误差相较于数据处理前略有增加。说明经过奇异谱分析后，SVM模型的模拟预测精度显著提升，尤其对于年最大径流的预测，而对于枯水期的模拟预测未有明显改进。
3.2.3. LSSVM模型模拟预测结果
由表3得出，数据预处理前，LSSVM模型率定期和检验期的模型效率系数分别为43%和38%，检验期的年均最大和最小径流相对误差分别高达31%和64%，说明模型对洪水和枯水的预测能力不足。通过对原始输入数据序列采用SSA去除噪声后，将得到的重建序列作为模型的输入进行预测，模型在检验期的纳什效率系数达到84%，水量平衡系数也较预处理前更接近于1；检验期的年均最大径流相对误差从原有的31%降低到9%，预测精度显著提升，年均最小径流相对误差也从64%降低到59%，有所改进。从图5可以直观地看出，数据未处理前，LSSVM模型预测值与实测值的总体趋势一致，但汛期的预测值与实测值偏差较大，尤其在2002年、2007年和2008年三年的洪峰处最为明显，模型预测结果较差，而经过数据预处理后，模型的预测值与实测值拟合较好，对汛期的到达时刻和峰值模拟的较为准确，同时较好地模拟出了2000年、2002年、2003年、2008年四年的双峰规律，说明经过奇异谱分析后，模型的预报精度显著提高。
4. 结论
本文以水布垭水库1951~2009年的月径流资料为依据，采用奇异谱分析对其进行数据预处理，选用SAR(1)模型、SVM模型和LSSVM模型作为径流预测模型，对原始序列和重建序列进行模拟预测。经过分析比较，可以得出以下几条结论：
1) LSSVM模型的模拟预测精度高于传统的SAR(1)模型，略低于SVM模型，但SVM模型和LSSVM模型对月径流极大值和极小值的预测误差仍然偏大。
2) 奇异谱分析是一种有效的数据预处理技术，经过预处理后的系列可以显著地提高SVM模型和LSSVM模型的模拟预测精度。
3) SSA-LSSVM模型的模拟精度最好，率定期和检验期的模型效率系数分别达到89%和84%，尤其表现对年最大月径流的预测，显著地提高了水布垭水库中长期径流预报水平。
基金项目
国家自然科学基金重点项目(51539009)和十三五国家重点研发项目(2016YFC0402206)资助。