1. 引言
随着感应发电机单机容量的增加和功率密度的提升,发电机在运行时单位体积内所产生的损耗也相应增大,从而引起发电机各个部分温度升高,影响了发电机的性能和寿命 [1] 。这就对发电机的冷却系统提出了越来越高的要求,需要对电机通风系统进行准确的计算 [2] 。因此对电机温度场进行仿真计算成为电机设计过程中必不可少的一个环节。
传统的温度场数值计算方法大多采用有限元法 [3] - [5] ,没有将传热过程和流体流动过程耦合计算,仿真计算结果误差较大 [6] [7] 。流体场数值计算方法通常将电机的整体结构分成若干部分,再对每一部分进行计算,难以获得工程分析所需要的整体、精确的计算结果 [2] 。本文采用有限体积法 [8] ,并采取一些简化处理方法,对3 MW感应发电机建立定子和转子的三维温度场和流体场的流固耦合模型,运用Fluent软件对电机定子和转子的温度场和流体场同时进行仿真计算。此仿真方法能够满足校核电机温度场的工程需求。
2. 发电机三维温度场的流固耦合模型
2.1. 发电机通风风路
本文提及的感应发电机采用闭式循环、双边进风的轴径向通风系统。冷却空气经离心风扇分三路进入电机内部,一路经气隙,进入定子铁心径向通风沟,再进入定子背部风道出风;另一路通过转子焊筋轴中间的通风孔,经转子铁心径向通风沟、气隙再进入定子铁心径向通风沟,再经定子背部风道出风;第三路过定子绕组端部,进入定子背部风道出风,这三路风在电机定子背部风道汇合后,经电机机座上面的冷却器冷却,再进入电机内部,形成闭式循环。
2.2. 仿真模型的简化处理方法
感应发电机的流固耦合模型简化处理方法 [9] 如下:
1) 根据电机定转子结构在圆周方向的周期对称性和轴向对称性,取电机轴向1/2,周向1/6作为仿真区域;
2) 定转子绕组内部的铜芯为多层铜线叠加而成,每层均包围有绝缘材料,在简化模型中,定转子绕组的内部全部为铜芯,外部包围有一层绝缘层,此简化对仿真结果的影响较小 [10] ;
3) 将结构复杂的定子端部绕组做拉直处理;
4) 仿真中忽略轴流风扇,直接设定进口边界条件;
5) 对电机内的一些细小部件做简化处理。
2.3. 物理模型的建立
在上述简化处理方法下,感应发电机的三维流固耦合物理模型如图1~3所示。
其中,各数字标号所代表的含义为:1表示冷却空气出口(冷却器),2表示背部风道,3表示定子端部空气,4表示冷却空气进风口,5表示转子端部空气,6表示定子径向通风沟,7表示转子径向通风沟,8表示气隙,9表示转轴间空气,10表示定子铁芯,11表示转子铁芯,12表示转轴,13表示定子绕组,14表示转子绕组,15表示端环。
2.4. 数学模型建立
在标准大气压下,发电机内流体的流动满足质量守恒和动量守恒,其三维控制方程 [11] 如下:
质量守恒方程为:
 (1)
(1)
式中:u、v、w分别为x、y和z方向上的速度分量。
动量守恒方程为:
 (2)
(2)
 (3)
(3)
 (4)
(4)
式中:ρ为流体密度;μ为动力粘度;p为流体压力。
湍流模型采用标准k-ε模型 [8] ,通过下述两个传输方程得到湍流动能k和扩散因子ε:
 (5)
(5)
 (6)
(6)
式中:μi为i方向流速;μ为动力粘度;Gk为当量速度梯度产生的湍流动能;σk、σε分别为k,ε对应的湍流普郎特数;μt为湍流粘性系数;C1ε,C2ε为常数。
基于传热学理论,发电机在直角坐标系下的稳态热传导方程 [12] 为:
 (7)
(7)
式中:T为温度,℃;λx、λy和λz分别为材料在x、y和z方向上的导热系数,W/(m·K);qv为热源密度,W/m3。
定子、转子表面及通风沟内通过对流换热,给出第三类边界条件:
 (8)
(8)
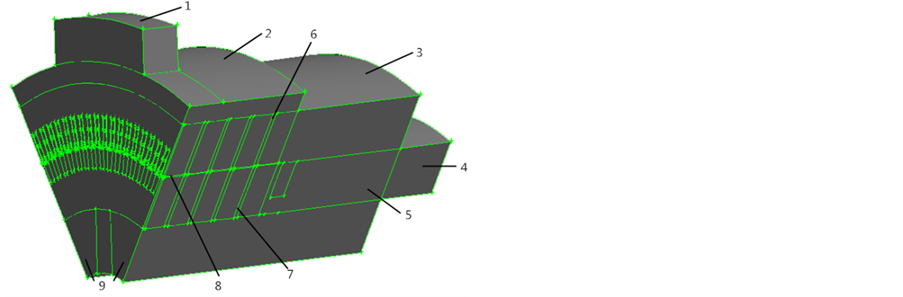
Figure 1. The fluid-solid coupled model for generator
图1. 发电机的流固耦合仿真模型
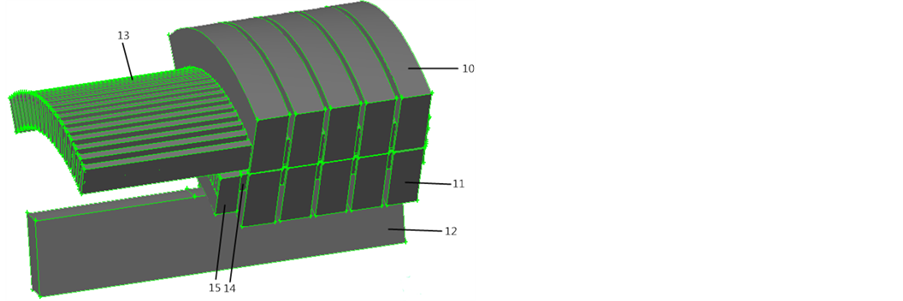
Figure 2. The solid fraction of the generator model
图2. 发电机仿真模型中的固体部分
Figure 3. Grid partioning of the model
图3. 仿真模型的网格划分
式中:n为定转子表面及通风沟内单位法向矢量;α为散热系数,W/(m2·K);Tf为空气温度,℃。
因此,求解域内三维稳态温度场边值问题为:
 (9)
(9)
2.5. 边界条件的设定
根据感应发电机的特点,在Fluent仿真平台上设定的边界条件 [8] [9] 如下:
1) 不计重力和浮力;
2) 不计辐射换热;
3) 发电机内流体流速远小于声速,故将其视为不可压缩流体;
4) 发电机内流体流路复杂多变且流速快,故采用标准k-ε模型;
5) 叠片结构的铁芯的传热系数设置为各向异性,其他结构的传热系数设置为各向同性;
6) 发电机轴对称面和圆周方向截面设置为对称面,其他边界面为无滑移边界;
7) 入口风速和入口初始温度根据发电机给定的总冷却风量和入口截面积确定,旋转区域的空气转速根据发电机额定转速确定。
3. 发电机定转子流体场仿真计算与分析
在电机定转子结构确定的情况下,通过调整发电机定子背部风路的风阻来分配风量和优化风阻。在多次仿真情况下,找出了较为优化的定子背部风道。发电机定转子整体的三维流体场仿真结果和发电机轴向、径向截面流体场仿真结果分别如图4~6所示。
在发电机定转子流体场的仿真计算中,忽略了定转子铁芯、定转子绕组、端环等固体部分发热的影响。在分析流体场时,主要考虑发电机内流体流速、发电机转子旋转产生的风扇作用、流体压力的分布
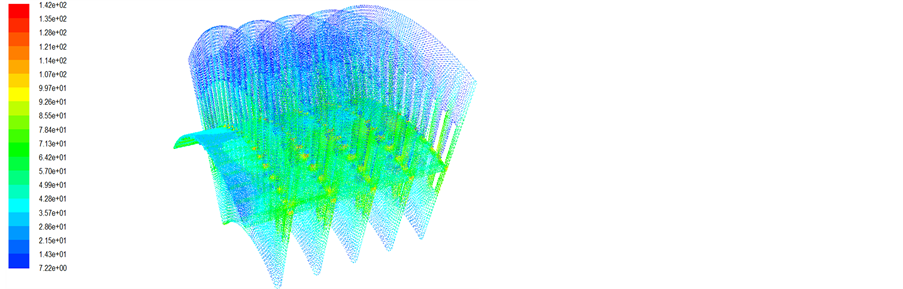
Figure 4. The simulation results for 3D fluid field of generator
图4. 发电机三维流体场仿真结果

Figure 5. The fluid field of generator axial section
图5. 发电机轴向截面流体场
情况等相关因素。
分析图4~6的仿真结果,可以发现发电机的气隙部分和定转子铁芯的径向通风沟部分风速相对较高。这主要是由于电机在设计中,气隙和定转子铁芯径向通风沟入口的过流面积极小,使气隙和定转子铁芯径向通风沟入口处的风阻很大,再加上转子以及转子槽口在旋转过程中起到了离心式风扇的作用,冷却空气从入口处被吸入,并在转子旋转作用下对冷却空气施加了动力,提高了冷却空气的压力和速度。被加速的冷却空气在流动过程中先将其动能转化为静压能,然后随着冷却空气压力的增大,又将其静压能转化为动能,从而驱动冷却空气在发电机内不断流动,这使得发电机能够得到有效的散热和冷却。
4. 发电机定转子温度场仿真计算与分析
在Fluent仿真平台上将发电机入口初始温度设为45℃时的定转子温度场仿真结果如表1所示。
分析表1中的仿真数据,相比较电机的其他结构而言,定子绕组的最高温度和平均温度均为最高,分别为111.4℃和95.6℃,其最大温升和平均温升也是最高。转子绕组和转子铁芯的温度相对较低,最高温度分别为69.5℃和67.5℃。温度场仿真结果与流体场仿真结果互相对应,可为电机的温度场优化提供一定参考作用。
电机定转子各部分的温度场分布云图分别如图7~11所示。
图7为电机整体的温度场分布云图,从中可以看出电机各个结构在全局温度范围内的分布情况。图8~11分别为电机定子绕组、定子铁芯、转子绕组、转子铁芯的温度场分布云图,其温度场分布与流体场分布相对应,定转子径向通风沟部分流速较高,靠近径向通风沟部分的温度相对较低,冷却效果较好。
另外,从图8和图10中可发现定子绕组端部和转子绕组端部温度相对较高,这是为了便于固定端部
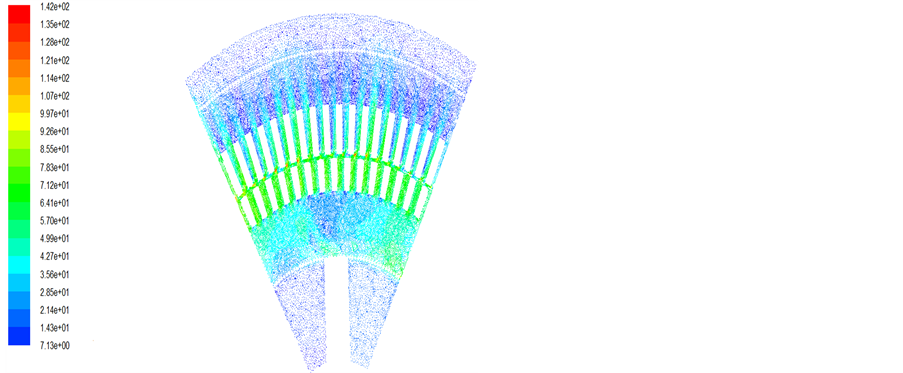
Figure 6. The fluid field of generator radial section
图6. 发电机径向截面流体场

Table 1. The temperature distribution for stator and rotor of the generation
表1. 发电机定转子各部分温度分布
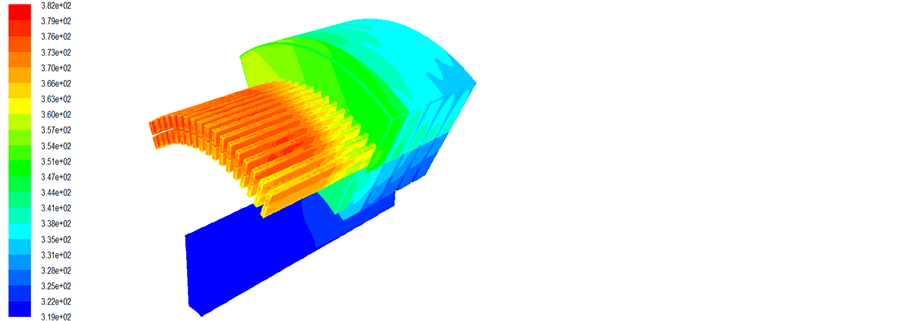
Figure 7. The temperature contour of the whole generator
图7. 电机整体温度场分布云图
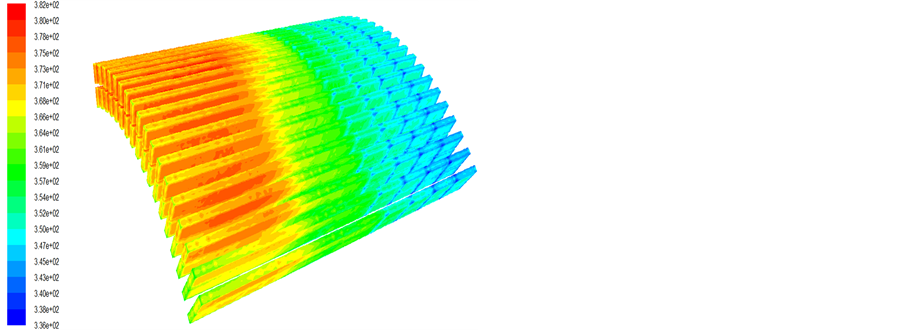
Figure 8. The temperature contour of the stator winding
图8. 电机定子绕组温度场分布云图
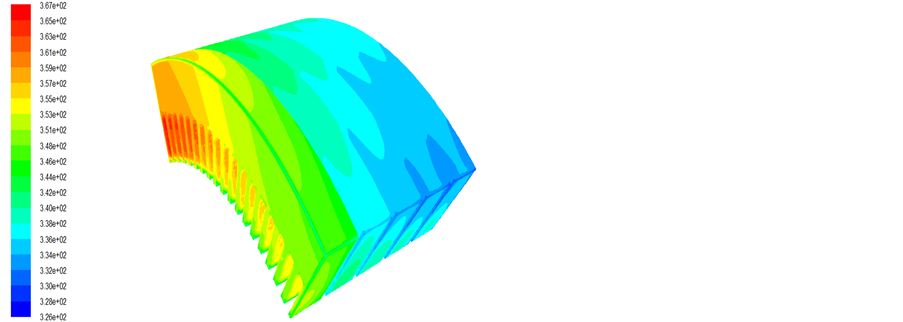
Figure 9. The temperature contour of the stator core
图9. 电机定子铁芯温度场分布云图
绕组,在各绕组之间用绝缘材料进行了填堵,使得导热系数较低,从而影响了散热,降低了冷却效果。由图9和图11可见,定转子铁芯的中间位置温度相对较高,通过分析可知,冷却空气进入转子铁芯径向通风沟后,在离心作用下流入气隙,故离冷却空气进风口位置越远的转子径向通风沟,其内部流动的空

Figure 10. The temperature contour of the rotor winding
图10. 电机转子绕组温度场分布云图
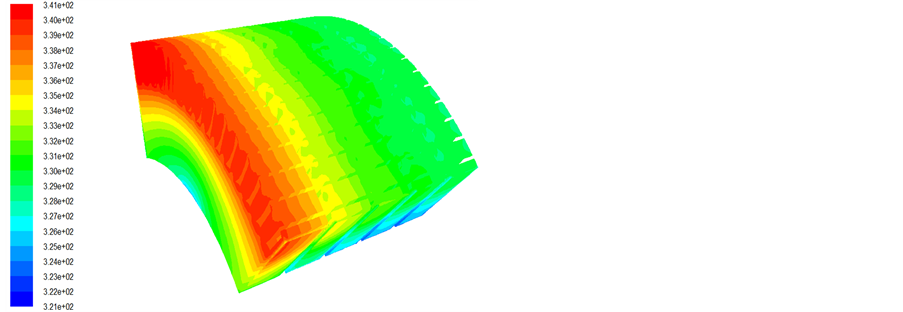
Figure 11. The temperature contour of the rotor core
图11. 电机转子铁芯温度场分布云图
气量越少,从而使转子铁芯的冷却效果越差,导致转子铁芯中间位置的温度较高;同理,从气隙流入定子径向通风沟的冷却空气亦受冷却空气进风口位置远近的影响,导致定子铁芯中间位置温度较高。
5. 结论
本文对3 MW感应发电机的三维温度场和流体场进行了仿真分析,仿真结果反映了电机内部温度场和流体场的分布情况,为电机冷却方案的设计和温度场优化提供了参考作用。