1. 引言
近年来,为了应对能源危机,分布式发电技术受到了广泛的关注。作为分布式发电技术的再发展,能够灵活的在并网与孤岛运行切换的微电网系统逐渐成为了行业内新的研究新方向[1] -[5] 。
当微电网处于并网运行状态时,分布式发电系统主要采用恒功率(PQ)控制方式。目前,对于PQ控制系统的等值模型,已经不少学者做了广泛研究[6] 。以正常并网状态的逆变器控制策略为依据,将微电网系统划分为不同节点,利用前推回代法求解系统状态[7] [8] 。指出在分析并网故障时要考虑补偿控制策略的影响,将DG等效为压控电流源模型,指出其存在电流饱和特性,并且分析了在对称与不对称故障下的系统状态特性,但是未考虑PQ控制逆变器存在的电压饱和特性。
当配电网由于故障等原因,使得微电网系统进入孤岛运行模式时,一般会有一个分布式发电系统或者储能装置采用恒压–恒频(VF)控制方式,向整个微电网系统提供电压与频率支撑,使的其他采用PQ控制的分布式系统能够继续正常工作[9] [10] 。指出由于大多数VF控制系统往往采用电压型并网逆变器,为了保证系统稳定,其直流侧一般都配有大电容,因此在分析其故障状态时主要从逆变器控制策略的角度出发[11] 。提出VF控制逆变器存在电压饱和特性,但是没有考虑到由于容量的限制,VF控制逆变器存在电流饱和状态。
本文在前人对于PQ和VF控制逆变器故障特性的分析基础上,通过数学推导,指出了PQ控制逆变器存在电压饱和与电流饱和两种极限状态。而VF控制的逆变器则存在恒压与电流饱和两种状态,推导了各个故障状态下的边界条件。利用PSCAD/EMTDC建立仿真模型,模拟在孤岛运行时发生三相短路故障下的电路暂态特性,并且求出了故障下的电压与电流的具体数值,通过仿真结果互相比较,验证本文所提出的方法的有效性。
2. DG的控制特性与等值模型
2.1. PQ控制器特性
在微电网处于并网运行的时候,DG一般采用PQ控制保证系统的功率平衡[12] 。给出了一种典型的PQ控制策略,如图1所示,可以让DG输出的有功和无功电流稳定于参考值,保证功率输出。
在dq0坐标系下PQ控制的逆变器注入电网的功率如公式(1)所示,根据瞬时无功理论,首先获取DG在并网点处的三相瞬时值电流Iabc与三相瞬时值电压Uabc,将Iabc与Uabc进行abc/dq0的帕克变换,并且同时选取d轴与ud矢量方向相同,使电压q轴分量为零,此时即可得到简化的公式(2),其中ud,uq,id,iq为逆变器出口侧的电压和电流经过dq0坐标变换之后的d轴分量和q轴分量。Pgrid,Qgrid,Pref和Qref分别为逆变器输出的有功无功的实际值以及参考值。正常工作时为实现能源的有效使用Qref一般为0。
 (1)
(1)
 (2)
(2)
对于PQ控制逆变器,故障点的位置,以及故障之后的等效阻抗,其对DG的输出有较大影响。如公式(3)所示,对于任意的逆变器,其并网连接处的电压受到逆变器出口侧的电压和滤波阻抗的影响。
 (3)
(3)
UDG为DG并网点的电压,EDG为DG出口侧电压,Z为等效滤波阻抗,IDG为逆变器输出电流,R为故障发生时的等效阻抗。参见图2,故障点所处的位置不同将导致故障发生时的等效电阻R发生改变。
若故障发生在f1处则,DG将失去大电网支持。 由公式(3)可知, 。在常规配电网中,风能,光伏等新能源,其能量变化具有一定的惯性,因此,可以认为故障前后的有功输出
。在常规配电网中,风能,光伏等新能源,其能量变化具有一定的惯性,因此,可以认为故障前后的有功输出 。由于
。由于 ,因此
,因此 。Z和Pref不会发生变化,
。Z和Pref不会发生变化, 大于1,故EDG和故障发生时的等效阻抗R成正比。文献[11] 指出当DG采用SPWM正弦脉冲宽度调制时,逆变器出口侧的
大于1,故EDG和故障发生时的等效阻抗R成正比。文献[11] 指出当DG采用SPWM正弦脉冲宽度调制时,逆变器出口侧的
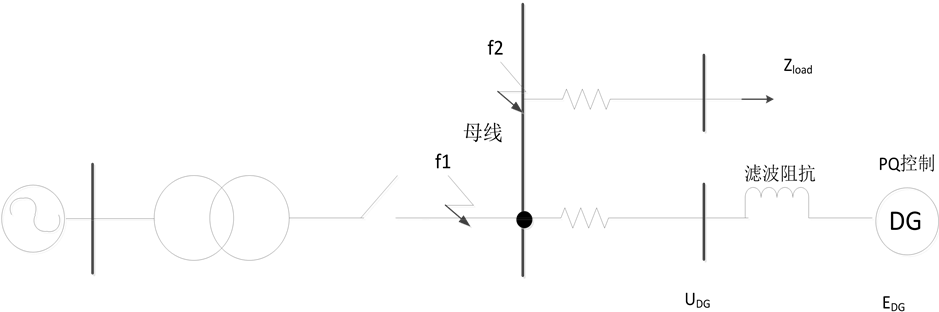
Figure 2. PQ control structure diagram
图2. PQ控制结构图
电压有效值由调制系数Pm和逆变器直流侧的电压UDC共同决定,其中 ,
, ,因此当在不同位置发生故障时存在电压饱和阻抗REMAX,导致
,因此当在不同位置发生故障时存在电压饱和阻抗REMAX,导致 ,使得
,使得 。由于Qref
。由于Qref
一般很小或者为0可以在发生故障之后维持不变,可得PQ控制DG在 ,电压处于饱和状态下的特性,如公式(4)所示:
,电压处于饱和状态下的特性,如公式(4)所示:
 (4)
(4)
当 时,由于电压幅值的限制EDGMAX维持不变,则电流IDG将会减小,最终导致功率输出降低。
时,由于电压幅值的限制EDGMAX维持不变,则电流IDG将会减小,最终导致功率输出降低。
如果故障位置的改变,如移动到f2位置处,等效阻抗R减小,而且此时仍有上级电网的支持,则根据 可知
可知 与
与 会减小,实际的有功输出Pout会瞬时一并减少,因此
会减小,实际的有功输出Pout会瞬时一并减少,因此 会增大,
会增大, 会变大,最终导致IDG电流变大。文献[12] 指出考虑到逆变器的中电力电子元件的耐压承受能力,会在PI控制环节对于对逆变器的最大输出电流作出限制,所以IDG存在大输出电流
会变大,最终导致IDG电流变大。文献[12] 指出考虑到逆变器的中电力电子元件的耐压承受能力,会在PI控制环节对于对逆变器的最大输出电流作出限制,所以IDG存在大输出电流 。随着f2所处的位置不同,存在电流饱和阻抗RIMAX,当故障电阻
。随着f2所处的位置不同,存在电流饱和阻抗RIMAX,当故障电阻 ,当电流达到饱
,当电流达到饱
和,最终将导致输出功率无法跟随参考值变化而减小。所以故障发生时的,等效阻抗大于 时,DG的输出特性可以用公式(2)与公式(3)描述,此时功率可以正常输出。当等效阻抗大于
时,DG的输出特性可以用公式(2)与公式(3)描述,此时功率可以正常输出。当等效阻抗大于 时,PQ控制的DG电流达到饱和,此时的输出特性可以描述为公式(5):
时,PQ控制的DG电流达到饱和,此时的输出特性可以描述为公式(5):
 (5)
(5)
本节基于电力系统仿真软件PSCAD/EMTDC,参照图2,搭建了一个的简单仿真模型。其中微电网正常工作电压为311 V,直流侧的电压UDC= 1000 V,滤波电路的电感L = 2 mH,滤波电容C = 10 uF,线路发生故障后的等效阻抗R分别为21 Ω,25 Ω,3 Ω与1 Ω。Pref= 17 kW,Qref= 0 kVar。参见图3与图4可见,
在0.5秒的时候发生三相短路故障,此时由上面的分析可知,若EDG达到饱和的峰值应等于 ,
,
与图3显示的仿真数据吻合,并且从图3,图4以及图5可以看出随着等效故障电阻 ,DG的输出电流IDG变小。最终导致了功率无法跟随参考值输出。而图6,图7以及图8,则反映了
,DG的输出电流IDG变小。最终导致了功率无法跟随参考值输出。而图6,图7以及图8,则反映了 ,以及
,以及 时,EDG减小,IDG增大直至饱和,以及功率输出从跟随参考值,到无法维持稳定的过程。
时,EDG减小,IDG增大直至饱和,以及功率输出从跟随参考值,到无法维持稳定的过程。
2.2. 恒压恒频控制(VF控制)模式输出特性分析
恒压恒频控制也称为VF控制,其作用是在微电网进入孤岛运行失去大电网的电压与频率支撑之后,
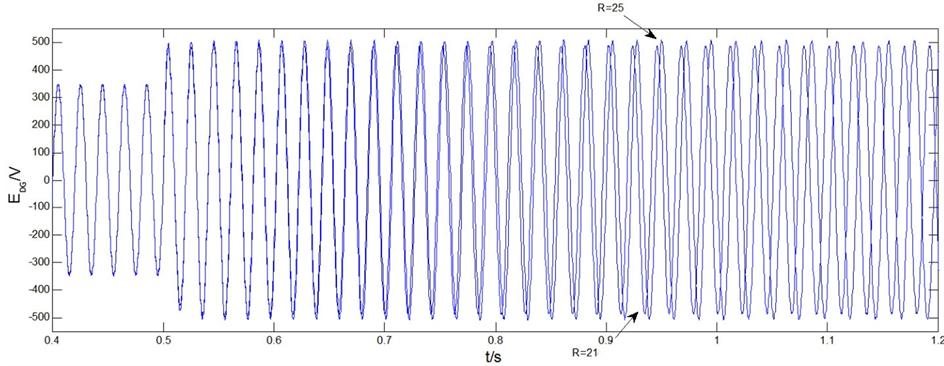
Figure 3. EDGvoltage (equivalent fault resistance = 21, resistance = 25 Ω)
图3. EDG电压(等效故障阻抗R = 21,R = 25 Ω)
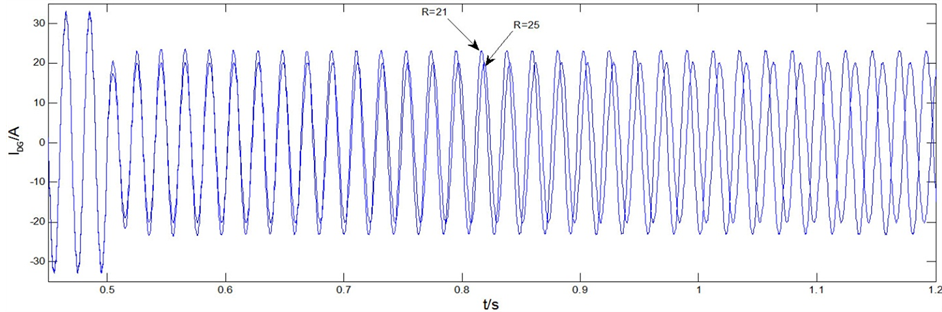
Figure 4. Inverter output current IDG(equivalent fault R = 21, R = 25 Ω)
图4. 逆变器输出电流IDG(等效故障阻抗R = 21,R = 25 Ω)
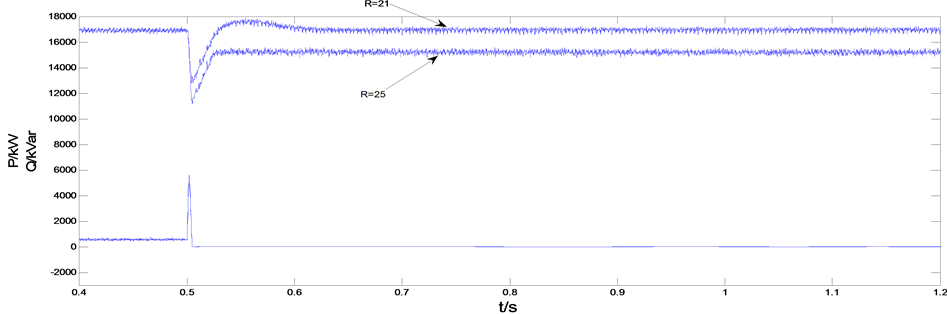
Figure 5. Inverter output power (equivalent fault R = 21, R = 25 Ω)
图5. 逆变器输出功率(等效故障阻抗R = 21,R = 25 Ω)
充当电压与频率的参考源。其结构如图9所示,其中参考频率信号f来自虚拟锁相环(PLL),与系统频率f相比较通过积分环节获得参考相角信号θ,并且结合参考电压Uref给出电压参考值Udref与Uqref。经过带限幅的PI调节之后获得内环电流参考值,并通过最终改变正弦脉冲宽度调制系数,调节逆变器并网点的电压。
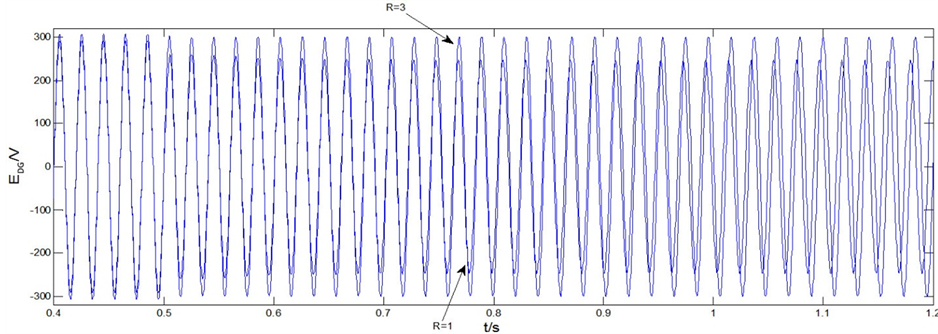
Figure 6. EDGvoltage (equivalent fault R = 1, R = 3 Ω)
图6. EDG电压(等效故障阻抗R = 1,R = 3 Ω)
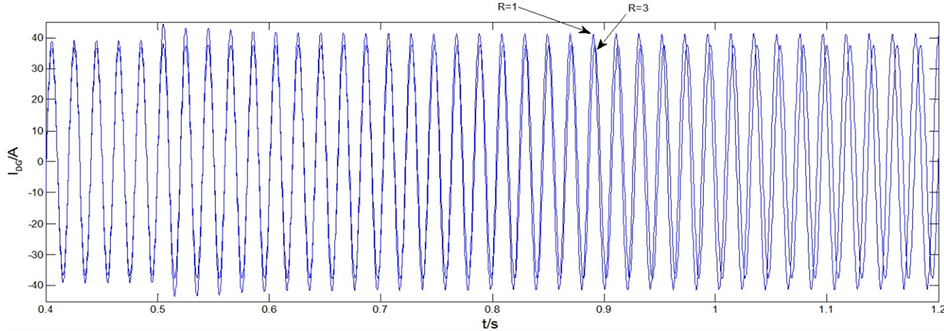
Figure 7. Inverter output current IDG(equivalent fault R = 1, R = 3 Ω)
图7. 逆变器输出电流IDG(等效故障阻抗R = 1,R = 3 Ω)
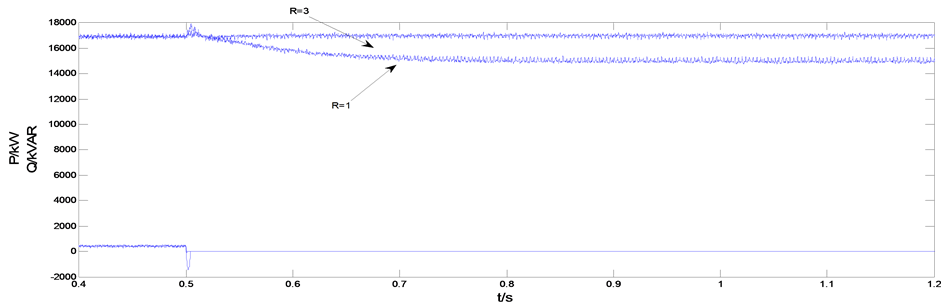
Figure 8. Inverter output power (equivalent fault R = 1, R = 3 Ω)
图8. 逆变器输出功率(等效故障阻抗R = 1,R = 3 Ω)
对于VF控制的逆变器,其输出基本特性仍然可以用公式(3)描述。上文已经指出 ,
,
但所不同的是,由于VF控制的逆变器其作用是维持电压等于Uref,因此在发生故障的时候 不会像PQ控制器一样达到EDGMAX,但是由于容量的限制逆变器也存在最大电流Ivfmax。与PQ控制逆变器不同,
不会像PQ控制器一样达到EDGMAX,但是由于容量的限制逆变器也存在最大电流Ivfmax。与PQ控制逆变器不同,
在稳定电压和频率的同时,VF控制的DG输出的功率具有较大的波动性,可以在一定程度上补偿微电网的功率不平衡。而且对于确定容量上限的逆变电源其Ivfmax往往也是可以确定的。VF控制的逆变器输出特性分为两种状态:电压恒定状态与最大电流饱和状态。分别如公式(6)与公式(7)所示:
1) 电压恒定工作状态
 (6)
(6)
当DG输出特性如公式(10)所示,则说明故障等效阻抗R比较大,故障电流未达到DG输出电流的极限,因此电压和频率都能够稳定与参考值。
2) 最大电流饱和状态
 (7)
(7)
由公式(7)可知,由于故障等效电阻R的进一步变小,导致DG输出的电流达到饱和,所以存在一个
临界电阻RL,当 是,
是, ,若
,若 ,则
,则 ,
, 。因此UDG会变小,同
。因此UDG会变小,同
时由于 ,EDG也会变小。一般而言发生此类故障的原因是,故障点接近逆变器出口侧,此时逆变器的输出电流达到控制的极限,无法实现整个微电网内部的功率平衡,会进一步导致微电网内部电压和频率偏离参考值,导致系统无法正常运行。
,EDG也会变小。一般而言发生此类故障的原因是,故障点接近逆变器出口侧,此时逆变器的输出电流达到控制的极限,无法实现整个微电网内部的功率平衡,会进一步导致微电网内部电压和频率偏离参考值,导致系统无法正常运行。
基于电力系统仿真软件PSCAD/EMTDC,参照图10,搭建了一个的简单仿真模型。其中微电网正常工作电压为311 V,直流侧的电压UDC= 750 V,滤波电路的电感L = 2 mH,滤波电容C = 10 uF,线路发生故障后的等效阻抗R为分别为10 Ω,8 Ω与2 Ω,。参见图11与图12可见,在1秒的时候发生三相短路故障。
从图11可以看出在故障发生之前,电压都稳定在正常值311V,而在1秒发生故障之后R = 2 Ω,R = 8 Ω的线路出口侧电压EDG与DG并网点电压UDG都减小,同时等效电阻R越小,电压跌落越多。而R = 10 Ω的线路电压没有发生跌落。从图12可以看出R = 2 Ω,R = 8 Ω的线路输出电流经过PI暂态积累调解的过程之后最终重合,达到了饱和电流Ivfmax,而R = 10 Ω的线路,虽然电流也有变大,但是最终输出电流并没有达到饱和电流Ivfmax,因此以电流IDG是否饱和,以及UDG,EDG是否跌落作为区分VF控制的DG所处的工作状态的边界条件是有效与合理的。
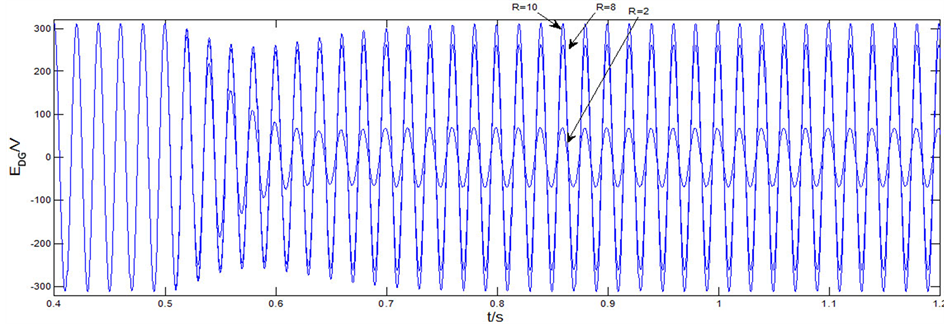
Figure 11. EDGvoltage of VF control (equivalent fault R = 10, R = 8 Ω, R = 2 Ω)
图11. VF控制下EDG电压(等效故障阻抗R = 10,R = 8 Ω,R = 2 Ω)
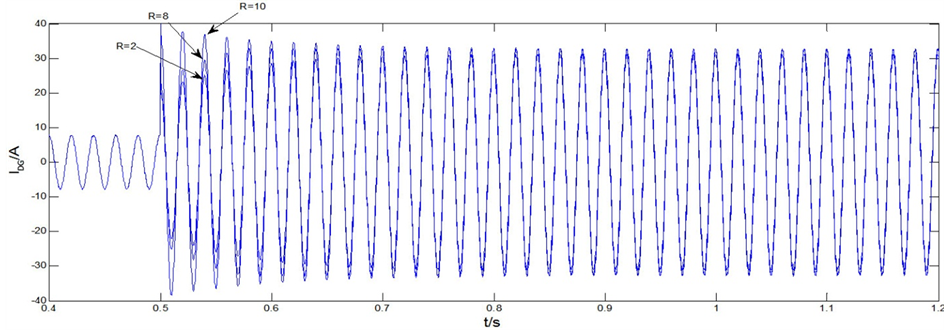
Figure 12. Inverter output current IDGof VF control (equivalent fault R = 10, R = 8 Ω, R = 2 Ω)
图12. VF控制逆变器输出电流IDG(等效故障阻抗R = 10,R = 8 Ω,R = 2 Ω)
3. DG的三相短路故障分析与验证
前面分析了只含有1种控制方式的DG在发生故障时候的特性,这一节将考虑有VF与PQ控制DG在孤岛运行时,发生故障下的综合特性。
在发生故障时候,故障分析与故障发生点的位置有关。根据图13可以得到公式(8)。
 (8)
(8)
如图13所示,在微电网线负载侧发生三相短路故障。ZS1和ZS2是等效滤波阻抗,Zl1,Zl2与Zl3是等效线路阻抗,故障发生时候的等效阻抗为Zf。尽管由于孤岛运行系统没有大电网的支持,但是由于VF控制的DG对与整个系统的输出电压与频率有支撑作用,因此PQ控制与VF控制DG只能处于以下三种工作状态。
1) VF控制DG能够稳定电压,PQ控制DG能稳定输出额定功率,此时可根据公式(2),公式(3),公式(6)与公式(8)求解故障电路。
2) VF控制DG不能够稳定电压,处于电流饱和状态,PQ控制DG能稳定输出额定功率,此时可根据公式(5),公式(7)与公式(8)求解故障电路。
3) VF控制DG 与PQ控制DG都处于电流饱和状态,此时可根据公式(5),公式(7)以及公式(8)求解故障电路。
4. 算例验证
为了验证特性方程的合理性,利用PSCAD/EMTDC软件按照图13的结构搭建了1个仿真系统。其中VF控制DG的参考电压为311V,PQ控制DG的参考功率Pref= 20 kW,Qref= 0 kVar。滤波电路电感L = 2 mH,滤波电容C = 10 uF,等效线路阻抗 ,
, ,
, ,
, 。故障发生时的等效故障阻抗Zf= 3Ω以及5 Ω,结果如表1与表2所示。
。故障发生时的等效故障阻抗Zf= 3Ω以及5 Ω,结果如表1与表2所示。
从表1可以看出,当Zf= 3 Ω,VF控制的DG输出电流已经达到饱和状态状态,因此其无法稳定电压,进而导致了UDG1小于参考值,而表2当Zf= 5 Ω,VF控制的输出电流小于Imax1,因此可以维持电压的稳定。由于精确的给出了包括DG电压Ud与Uq,输出电流Id与Iq分量的计算公式,因此可以计算包括相角在内的各个数值,并且仿真值与计算值的误差都小于3%。因此上述结果可以证明本文所推导的微电网运行分析方法,可以在考虑DG控制策略的前提下,有效分析故障下电路状态。

Table 1. Fault analysis results in microgrid (three-phase short circuit resistance Zf = 3 Ω)
表1. 当Zf= 3 Ω的微电网故障分析

Table 2. Fault analysis results in microgrid (three-phase short circuit resistance Zf = 5 Ω)
表2. 当Zf= 5 Ω的微电网故障分析
5. 结论
本文基于对PQ与VF控制DG的输出特性的分析,提出了故障状态分析模型,以及不同故障状态下的边界条件,主要体现在以下4个方面:
1) 对于采用PQ控制的DG,在输出状态随着故障等效电阻R的不同,以DG最大输出电压EDGMAX与最大输出电流IMAX,以及参考功率Pref和Qref作为划分故障状态的边界条件。当处于最大输出电压或者最大输出电流状态时,则输出功率无法保证。
2) 对于采用VF控制的DG,由于有参考电压的钳制,因此与PQ控制不同,只存有电压恒定于参考值状态,或者电流饱和状态,因此以Uref和IMAX,作为划分故障的边界条件。当处于电流饱和状态时,则系统的电压和频率将无法稳定。
3) 基于上述关于DG控制策略的故障特性分析,通过进行数学推导和特性方程的建立即可以从理论上计算出故障时的状态变量,而基于PSCAD/EMTDC的仿真则证明本文所分析的方法的正确性。
4) 微电网系统由于电流存在双向流动,而且是多个控制系统的互相耦合,因此分析较为复杂。本文所推导的关于PQ控制与VF控制逆变器的故障特性分析,在理清各个控制策略对于微电网系统影响的同时,将会有助于微电网系统继电保护研究与分析。