1. 引言
共形映射是复分析中的一个非常重要的内容,它在很多的科学技术领域有广泛的应用。特别在绘制地图、飞机设计、解决流体力学、弹性力学、电学等学科的实际问题中,都能使复杂问题简单化。近年来,随着计算机技术的发展,共形映射已广泛应用于辅助几何设计、图形图像设计等领域。共形映射具有一种非常重要的性质:旋转角不变性和伸缩率不变性,也就是说,几何图形经过共形变换后,它的整体外形发生改变,但是又局部的保持一定的刚体性质。这种刚性可以满足几何造型设计的中的刚性要求[2] 。例如:要研究飞机机翼剖面轮廓形状及它在空中飞行时所受阻力、上升力等,如按原图计算,会非常困难和复杂,如用共性映射把它映成单位圆则会变得比较简单,这种方法在飞机设计方面有重要应用。
既然共形映射有如此广泛的应用,我们自然会疑问:在扩充复平面上,任意给定两个单连通区域D与G,是否都能找到一个解析函数使D共形映射为G呢?这个问题当G为单位圆时,可通过黎曼存在与唯一性定理得到解决。我们这里要讨论的是如何从上半平面共形映射成预先给定的一个多角形区域。
下面我们分两个部分来介绍。第二部分给出从上半平面共形映射成预先给定的一个多角形区域的克里斯托费尔–施瓦茨变换定理及其它的三个退化变换形式,第三部分通过具体的例子分析克里斯托费尔–施瓦茨变换的应用,最后给出结论。
2. 克里斯托费尔–施瓦茨变换
2.1. 共形映射的定义 [1]
定义1:若函数 在点
在点 的邻域内有定义,且在点
的邻域内有定义,且在点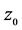 具有以下两个性质:
具有以下两个性质:
(1) 伸缩率不变性:即在点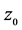 附近,像点间的无穷小距离与原像点的无穷小距离之比的极限
附近,像点间的无穷小距离与原像点的无穷小距离之比的极限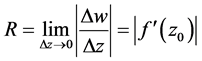 仅与
仅与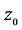 有关,与过
有关,与过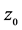 的曲线C之方向无关。
的曲线C之方向无关。
(2) 过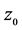 的任意两曲线的夹角在变换
的任意两曲线的夹角在变换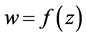 下,既保持大小又保持方向。
下,既保持大小又保持方向。
则称函数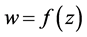 在点
在点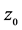 是保角的。
是保角的。
定义2:若函数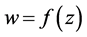 在区域D内单叶且保角,则称
在区域D内单叶且保角,则称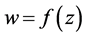 是D内的共形映射。
是D内的共形映射。
2.2. 克里斯托费尔–施瓦茨变换
下面给出克里斯托费尔–施瓦茨变换定理[1] ,它给出了我们把上半平面共形映射成预先给定的一个多角形区域的解析函数。在此,我们仅给出定理的内容,其证明可参看[1] 第八章第四节。
定理1:设(1)有界n角形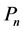 的顶点分别为
的顶点分别为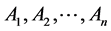 ,其对应顶角为
,其对应顶角为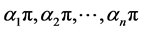 ,
, ;
;
(2) 函数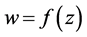 将上半平面
将上半平面 共形映射成
共形映射成 ;
;
(3) 平面实轴上对应于
平面实轴上对应于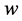 平面多角形
平面多角形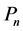 的顶点
的顶点 的那些点
的那些点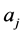 :
:
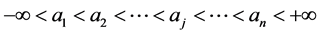
都是已知的。则
 (1)
(1)
其中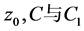 是三个复常数。
是三个复常数。
注意到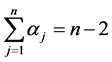 ,且(1)的逆变换
,且(1)的逆变换 将
将 平面上的单连通区域多角形
平面上的单连通区域多角形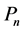 共形映射成标准区域上半
共形映射成标准区域上半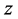 平面。
平面。
推论1(退化的克里斯托费尔–施瓦茨变换):当n角形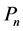 有一个顶点是无穷远点的像,即
有一个顶点是无穷远点的像,即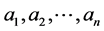 中有一个如
中有一个如 ,则在公式(1)中丢掉那个关于这个顶点的因子即可,即
,则在公式(1)中丢掉那个关于这个顶点的因子即可,即
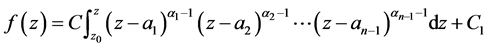 (2)
(2)
推论2(广义多角形的克里斯托费尔–施瓦茨变换):设n角形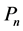 有一个或几个顶点在无穷远点,不妨设有一个如
有一个或几个顶点在无穷远点,不妨设有一个如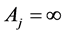 ,则公式(1)仍成立,只需要把顶点在无穷远处的那两条直线间的角度,用这两条直线在有限点处的那个夹角反号代替。
,则公式(1)仍成立,只需要把顶点在无穷远处的那两条直线间的角度,用这两条直线在有限点处的那个夹角反号代替。
推论3(把单位圆变成n角形的变换[3] ):把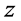 平面上的单位圆
平面上的单位圆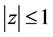 变成
变成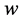 平面上的n角形
平面上的n角形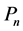 的共形映射是:
的共形映射是:
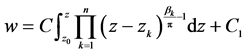
其中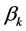 是
是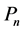 的各顶角的弧度,
的各顶角的弧度, 是单位圆周
是单位圆周 上与
上与 的各顶点相对应的点。
的各顶点相对应的点。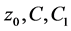 是复常数。
是复常数。
3. 应用举例
很多工程、地图绘制中都会涉及到多角形区域,故研究多角形区域的共形映射是很重要的内容,下面我们给出几种应用上述各推论的多角形区域共形映射的例子。
例1:将上半平面 共形映射成
共形映射成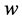 平面上如图1的广义多角形区域:
平面上如图1的广义多角形区域:
解:把w平面中的区域看成是有四个顶点A1、A2、A3、A4的广义多角形,两个顶点A2与A4在无穷远。我们选取 对应于顶点A3,
对应于顶点A3,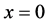 对应于顶点A1,
对应于顶点A1,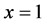 对应于顶点A2,
对应于顶点A2,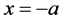 对应于顶点A3。这时四个顶点A1、A2、A3、A4分别对应
对应于顶点A3。这时四个顶点A1、A2、A3、A4分别对应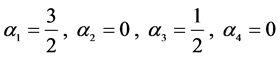 ,得到如表1的表格:
,得到如表1的表格:
由克里斯托费尔–施瓦茨的两个推论有:

由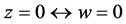 得:
得:
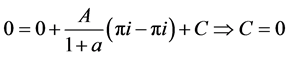
又当z在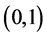 上变化时,对应的点w应在正虚轴的
上变化时,对应的点w应在正虚轴的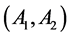 上变化。
上变化。
取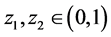 ,则对应的
,则对应的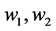 应为纯虚数。
应为纯虚数。
 (3)
(3)

Figure 1. The conformal mapping from polygonal domain of pipeline
图1. 管道型多角区域共形映射

Table 1. The data of conformal mapping from the polygonal domain of pipeline
表1. 管道多角区域共形映射的数据对应表
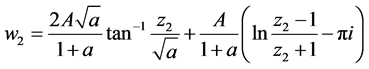 (4)
(4)
由(3)~(4),再注意到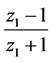 或
或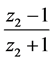 的辅角均为
的辅角均为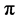 ,则
,则
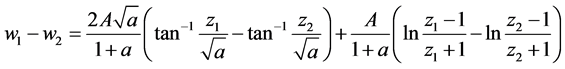
上式左边为纯虚数,右边也为纯虚数,故A为纯虚数,不妨设为 (
( 为实数)。
为实数)。
又因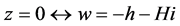 ,则
,则
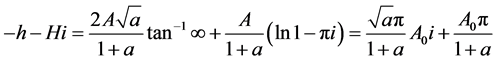
比较上式两端,可得
 (5)
(5)
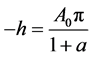 (6)
(6)
由(5) (6)可知
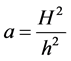 ,
,
则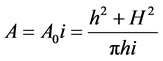 。
。
故所求保形映射为:
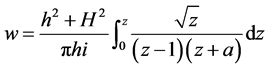
例2:求把图2中上半z平面变成w平面上的如图2区域的共形映射,对应点如图2所示。
解:把w平面中的区域看成是有三个顶点B1、B2、B3的广义多角形,两个顶点B2与B3在无穷远。我们选取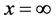 对应于顶点B3,
对应于顶点B3,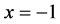 对应于顶点B1,
对应于顶点B1,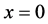 对应于顶点B2。这时在顶点B1,
对应于顶点B2。这时在顶点B1, ;在顶点B2,
;在顶点B2,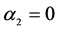 ;在顶点B3,
;在顶点B3,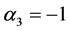 。故由题意可以得到如表2的各点的对应关系:
。故由题意可以得到如表2的各点的对应关系:
由克里斯托费尔–施瓦茨的两个推论有:

为了确定常数A和C,把上式改写为:
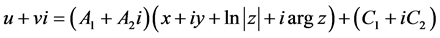 (7)
(7)
比较两端虚部得:
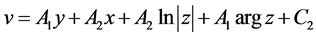 (8)
(8)
当w沿AB趋于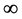 时,
时,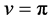 ,这时z沿实轴从–1趋于0,于是
,这时z沿实轴从–1趋于0,于是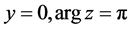 ,于是由(8)知
,于是由(8)知
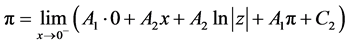
为使上式成立,A2必为0,故
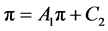 (9)
(9)
又当w沿OB趋于 时,
时,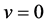 ,这时z沿正实轴趋于0,于是
,这时z沿正实轴趋于0,于是 ,于是由(8)知
,于是由(8)知
 (10)
(10)
由(9)与(10)知 ,那么
,那么 ,所以
,所以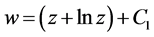 ,最后由对应关系
,最后由对应关系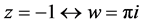 ,有
,有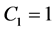 。
。
综上所述,共形映射为: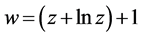
例3:求把图3中z平面上的单位圆变成w平面上的如图3的正方形区域的共形映射,对应点如图3所示。
解:由题意以及推论3可知,z平面上各点与w平面中正方形各顶点有如表3的对应关系:

Figure 2. The conformal mapping from polygonal domain of upper half plane cutting by ray
图2. 沿射线割破平面的多角区域共形映射

Table 2. The data of the conformal mapping from polygonal domain of upper half plane cutting by ray
表2. 沿射线割破平面的多角区域共形映射数据对应表

Figure 3. The conformal mapping from unit circle to square
图3. 单位圆共形映射为正方形

Table 3. The data of conformal mapping from unit circle to square
表3. 单位圆共形映射为正方形的数据对应表
由推论3的结论有:
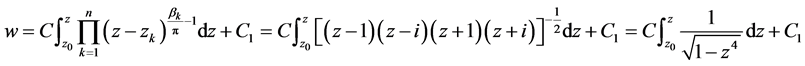
根据对应关系:
 有:
有:
 (11)
(11)
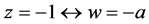 有:
有:
 (12)
(12)
则(11)~(12)得:

由留数定理可解得:
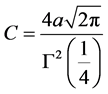
根据(11)+(12)得:
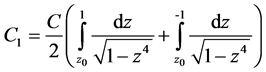 (13)
(13)
又根据对应关系:
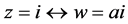 有:
有:
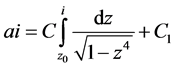 (14)
(14)
 有:
有:
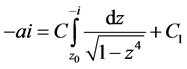 (15)
(15)
则(14)+(15)得:
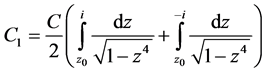 (16)
(16)
联立(13)与(16)可得:
再把 及
及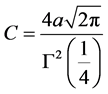 代入(13),立即得到
代入(13),立即得到 。
。
综上所述,由单位圆到正方形的共形映射为:
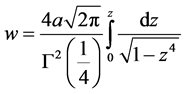
4. 结论
本文主要讨论了使上半平面映射为多角形区域的共形映射的形式。实际上,共形映射可以解决很多其他领域的问题,比如地图绘制、零件的构造、人脸识别等等方面,随着计算机技术的不断发展,共形映射的作用越来越广泛。