1. 引言
BP网络是一种反向传播网络,是对线性可微分函数进行权值训练的多层网络。BP网络在模式识别方面有很重要的应用。像缺失二维码的识别、图像的识别、车牌识别等方面都广泛应用BP网络。这个网络具有高度的非线性运算性,不同的输入与输出的的对应,使网络更加灵活。本文应用BP网络对图片的特征进行识别,得到很好的结论。识别效率在80%。
矩函数 [1] 在图像分析 [2] 中有着广泛的应用,如模式识别 [3] 、目标分类、目标识别与方位估计、图像编码与重构等。本文主要应用的是其在模式识别方面的应用。一个从一幅数字图形中计算出来的矩集,通常描述了该图像形状的全局特征,并提供了大量的关于该图像不同类型的几何特性信息,比如大小、位置、方向及形状等。图像矩的这种特性描述能力被广泛的应用在各种图像处理、计算机视觉和机器人技术领域的目标识别与方位估计中。一阶矩与形状有关,二阶矩显示曲线围绕直线平均值的扩展程度,三阶矩则是关于平均值的对称性的测量。由二阶矩和三阶矩可以导出一组共七个不变矩。不变矩是图像的统计特性,满足平移、伸缩、旋转均不变的不变性,在图像识别领域得到了广泛的应用。
投影能表现图像的某种特征信息,指定方向上单条前景像素的个数。本文主要做了垂直方向的势能和水平方向的势能。
2. BP网络原理 [4]
2.1. BP网络模型
图1中P表示输入,从图中可以看出这个网络有r个输入,共有q组这样的输入。W1表示隐表示输出层的权值,B2表示输出层的误差。k输出层第k个神经元的实际输出,F2表示输出层的激活函数。从图中可以看出,输出层的输入是s1维的,输出层也有q组这样的输入。
2.2. 节点输出
节点的输出主要是包括隐含层和输出层节点的输出,其实两者的输出是一致的,都是前层节点的输
出加和再加上误差的影响,如下:
隐节点输出模型:
 (1)
(1)
其中 表示隐含层的输出。
表示隐含层的输出。
输出节点输出模型:
 (2)
(2)
其中 表示输出层的输出。
表示输出层的输出。
2.3. BP网络的激活函数
BP网络经常是有的是S型的对数或正切激活函数和线性函数。因为S型函数具有非线性放大系数功能,它可以把输入从负无穷大到正无穷大的信号,变换成−1到1之间的输出。对较大的输入信号,放大系数较小;而对较小的输入信号,放大系数则较大。所以采用S型激活函数可以处理和逼近非线性的输入/输出关系。不过,如果在输出层采用S型函数,输入则被限制到一个很小的范围;若采用线性激活函数,则可采用网络输入任何值。所以只有当希望对网络的输入进行限制,如限制在0和1之间,那么在输入层应当包含S型激活函数,在一般情况下,均是在隐函数采用S型激活函数,而输入层采用线性激活函数。
2.4. 误差的反向传播
误差计算模型是反映神经网络期望输出与计算输出之间误差大小的函数:
 (3)
(3)
2.5. BP网络的学习规则
BP算法是一种监督式的算法。主要是通过输入样本,通过网络得到的实际输出样本和已知与输入样本对应的输出样本之间的误差来修正权值的。使得实际输出样本和已知的输出样本尽可能的接近,也就是使得网络的输出层的误差的平方和最小。它是通过连续不断地在相对于误差函数斜率下降的方向上计算网络权值和偏差的变化而逐渐逼近目标的。每一次的全职和偏差的变化都与网络误差的影响成正比,并以反向传播的方式传播到前面的每一层。
3. 7个不变矩和字符势能
3.1. 二值字符的7个不变矩(Hu矩)特征
在连续情况下,图像函数为 ,那么图像的p + q阶几何矩(标准矩)定义为:
,那么图像的p + q阶几何矩(标准矩)定义为:
 (4)
(4)
p + q阶中心距定义为:
 (5)
(5)
其中 和
和 代表图像的重心,
代表图像的重心,
 (6)
(6)
 (7)
(7)
对于离散的数字图像,采用求和号代替积分:
 (8)
(8)
 (9)
(9)
 和
和 分别是图像的高度和宽度;
分别是图像的高度和宽度;
归一化的中心距定义为:
 ;其中
;其中 (10)
(10)
利用二阶和三阶归一化中心矩构造了7个不变矩 :
:
 (11)
(11)
 (12)
(12)
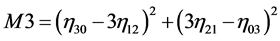 (13)
(13)
 (14)
(14)
 (15)
(15)
 (16)
(16)
 (17)
(17)
Hu. M. K在1962年证明了由这7个不变矩 [5] 构成一组特征量具有旋转,缩放和平移不变性。实际上,在对图片的识别中,并不是所有的Hu矩都保持三个特性,其实只有 和
和 不变性保持的比较好,剩下的几个不变矩对不变性带来的误差就比较大了,有学者认为只有基于二阶矩的不变矩对二维物体的描述才是真正的具有旋转、缩放和平移不变性(
不变性保持的比较好,剩下的几个不变矩对不变性带来的误差就比较大了,有学者认为只有基于二阶矩的不变矩对二维物体的描述才是真正的具有旋转、缩放和平移不变性( 和
和 刚好都是由二阶矩组成的)。
刚好都是由二阶矩组成的)。
由Hu矩组成的特征量对图片进行识别时,避免了用图片直接进行识别所引起的信息量大,从而速度很快,但是也存在一些缺点,比如识别率比较低,因为图片的特征量不能很好的反应图片的本质。对于纹理丰富的图片,像手势识别 [6] ,识别就很低。由于Hu不变矩只用到低阶矩(现在最多三阶矩),所以并不能对图像的细节描述清楚,图像的特征量不明显。
Hu不变矩一般用来识别图像中大的物体,对于物体的形状描述得比较好,图像的纹理特征不能太复杂,像识别水果的形状,或者对于车牌中的简单字符的识别效果会相对好一些。
3.2. 二值字符的字符势能投影特征
针对以往字符投影(见图2)的密度统计特征的不足,我们进行字符势能特征提取 [7] ,下面简要介绍一
下字符势能。
最后我们得到的特征数据是:

4. 识别过程
图片的势能有垂直方向势能(见图3)和水平方向势能(见图4),本文提取了手写体数字图片的7个不变矩以及每张图片的字符势能,然后对提取的这两方面的特征向量再求均值、方差等,下面我们看一下几幅图的特征和字符时能:
我们选取两副图片,来看看他们的不变距和字符时能。
我们选取的图片(见图5)都是从画图工具插入的 的图像。
的图像。
数字1的不变距特征:bubianju1 = [1.74809618654275; 13.0086683512297; 15.4218332622757;

Figure 2. Horizontal and vertical projection
图2. 水平和垂直方向投影

Figure 3. Potential in the vertical direction
图3. 垂直方向势能

Figure 4. Potential in the horizontal direction
图4. 水平方向势能
14.6951883042133; 30.6959439883039; 22.6999061621170; 29.7542843350497; 14.4311926605505; 14.5412844036697; 8.12073733243560; 8.18963636280428; 2.05369581043094; 3.46709986839808]。
图6显示的是数字1的不变距的13个特征的大小。
数字2的不变距特征:bubianju2 = [1.69054859157154; 11.0446320281519; 15.3965741740709; 15.7757991761264; 32.1016844108935; 21.6370923441087; 31.5191547719385; 14.4979423868313; 14.4622770919067; 8.11966197545053; 8.28834848639378; 2.10797164696553; 3.53488626570687]。
图7显示的是数字2的不变距的13个特征的大小。
可以看出,两幅图片的不变距特征都是13维的向量,为了能让我来识别,我们要对这些数字进行归一化处理,当然,这很好实现,只需找到数组中的最大值和最小值,然后数组中的各个数字减去最小值,比商最大值就能归一化到[0,1]这个区间。
下面,我们再来看一下图片的字符时能。

Figure 6. The distribution of moment invariants of number 1
图6. 数字1不变距的分布

Figure 7. The distribution of moment invariants of number 2
图7. 数字2不变距的分布
数字1的字符时能:zifushineng1=[406;406;406;406;406;406;393;393;393;393;393;393;393;393;393; 393;393;393;393;393;393;393;393;393;393;393;393;406;406;406;406;406;406;406;406;406;406;406;406;406;49;406;406;406;406;406;406;406;406;406;406;406;406;406;406;406;406;812;1218;1624;2030;2436;2842;3248;3654;4060;4466;4872;637;5684;6090;6496;6902;7308;7714;8120;8526;8932;9338;9744;10150;10556;10962;11368;28;56;84;112;140;168;196;224;252;280;308;336;91;392;420;448;476;504;532;560;588;616;644;672;700;728;756;784]。
图8显示的是数字1的字符时能的大小分布情况。
数字2的字符时能:zifushineng2 = [406;406;406;326;342;371;361;374;381;387;387;369;388;388;389;390; 375;392;392;393;394;368;175;359;406;406;406;406;406;406;406;406;406;389;398;371;378;356;356;357;358;342;362;346;364;322;326;383;383;383;359;382;406;406;406;406;406;812;1218;1624;2030;2334;2786;2968;3402;3560;3916;4284;4654;4788;5430;5536;6188;5796;6194;7660;8043;8426;8257;9168;10150;10556;10962;11368;28;56;84;112;140;156;189;200;234;250;275;300;325;336;375;384;425;360;399;540;567;594;598;648;700;728;756;784]。
图9显示的是数字2的字符时能大小的分布情况。
可以看出,他们都是112维的向量,其实通过我们家少的字符势能,我们能看出势能提取的大小。
5. 识别结果
我们再以不变矩、势能、以及求取的不变距的均值、方差等作为输入向量。用BP网络进行训练和仿真。在训练时,我们选取了200组图片,然后再以30组新的图片作为测试样本,进行识别。得到下面结果:
由表1可以看出,有些数字的识别效果很好,像数字1、2、3、4、6、7、8、9、0识别正确率都很

Figure 8. The distribution of potential energy of number 1
图8. 数字1势能的分布

Figure 9. The distribution of potential energy of number 2
图9. 数字2势能的分布

Table 1. The recognition correct rate of each number
表1. 各个数字的识别正确率
高,数字1、7、9的识别正确率都是100%,数字2、3、4、5、6、0的识别正确率也在80%以上,不过数字5的识别正确率很低,不到60%。主要是因为在输入的时候,数字5的输入不是很规范,而且数字5本身和数字3和8也有一定得相似性,导致你误识。但是,经过特征提取,数字总体的识别正确还是增加了很多,总体的识别正确率达到了86.36。
项目基金
2013年国家自然科学研究基金(编号:61275120)。