1. 引言
狄利克雷积分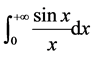 在工程技术,阻尼振动中有广泛的应用,其被积函数不能用初等函数表示,
在工程技术,阻尼振动中有广泛的应用,其被积函数不能用初等函数表示,
不能直接计算[1] -[3] 。文[4] 介绍了9种算法,大致是通过二重积分、级数、等式、收敛因子法计算出
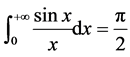 。本文介绍了四种狄利克雷积分证明方法,其中证法一和二是两种经典的证明方法[5] ,本
。本文介绍了四种狄利克雷积分证明方法,其中证法一和二是两种经典的证明方法[5] ,本
文对证法二进行了适当的改进,在一定程度上简化了其证明的复杂度;证法三和四是本文在传统证明方法的基础上,将复变函数与积分变化、傅里叶变换相结合提出的两种新的证明方法,与传统的证明方法相比,本文提出的方法较好的改善了狄利克雷积分证明的复杂度,而且在不同条件下都可进行有效的推广。本文介绍的狄利克雷积分的四种证明方法详细证明过程如下。
2. 传统的狄利克雷积分证明方法与改进
第一个证明方法是利用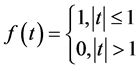 傅里叶积分表达式来证明。
傅里叶积分表达式来证明。
证明一:函数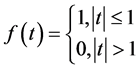 的傅里叶积分表达式为:
的傅里叶积分表达式为:
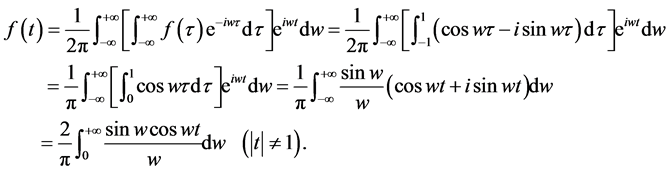
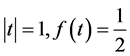 ,故
,故
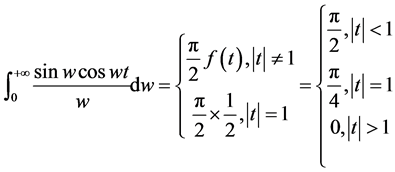 当
当 ,就有
,就有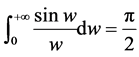 。
。
下面要介绍的第二种证法是用柯西–古萨定理和约当引理来证明。
证明二: 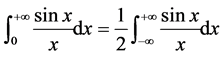 ,
,
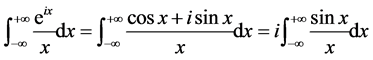 先考虑
先考虑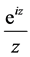 沿着下图的积分路径
沿着下图的积分路径
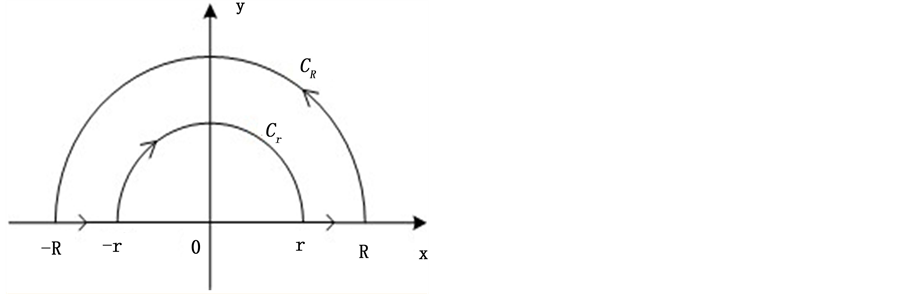
由柯西–古萨定理,有
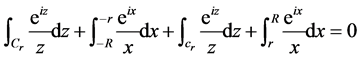
令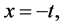 则有
则有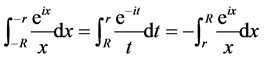 ,
,
所以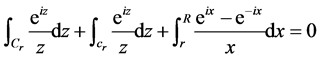 ,即
,即
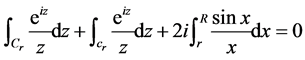 , (1)
, (1)
由约当引理二可知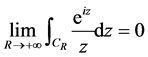 ,剩下只要求出
,剩下只要求出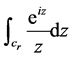 的值就可以了。
的值就可以了。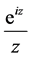 的洛朗展式为:
的洛朗展式为:
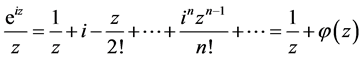 ,
,
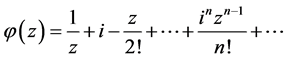 在
在 是解析的,
是解析的,
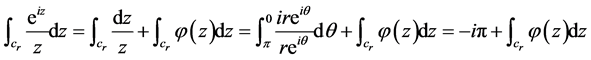
 ,当
,当 充分小时,
充分小时,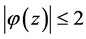 ,当r充分小时,
,当r充分小时,
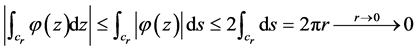 故
故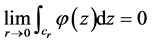 ,即
,即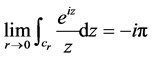 ,代入(2)式中有
,代入(2)式中有
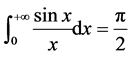
该证明方法比较复杂,上述证明中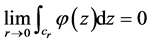 可以改良为如下证明:
可以改良为如下证明:
证明:因为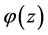 在整个复平面上处处解析,故其和积分路径无关,只与起点和终点有关,则
在整个复平面上处处解析,故其和积分路径无关,只与起点和终点有关,则
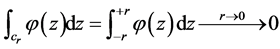 .
.
3. 基于复变函数与积分变换的狄利克雷积分证明
第三种证明方法是本文新提出的方法,利用像函数的积分性质进行证明,证明方法如下:
证明三:像函数的性质为:如果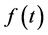 的拉普拉斯变换
的拉普拉斯变换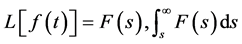 收敛,则
收敛,则
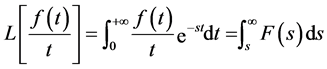 (2)
(2)
上式中令 得到:
得到: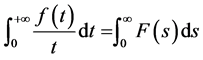 ,利用这个式子,令
,利用这个式子,令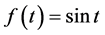 ,则有
,则有
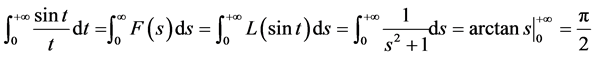
可以看出,基于像函数的性质进行证明非常简单,很大程度上简化了狄利克雷积分证明的复杂度。
4. 基于复变函数与积分变换的狄利克雷积分证明
本文提出的另一种方法是基于复变函数和傅里叶变换进行证明的,方法如下:
证法四: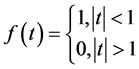 的傅里叶变换为
的傅里叶变换为
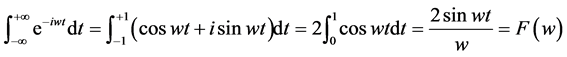
由傅里叶变换的对称性质: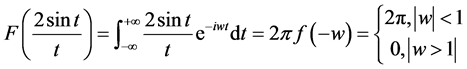
令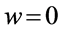 ,
,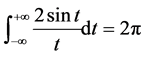 ,即
,即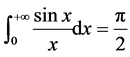 。
。
5. 结论
狄利克雷积分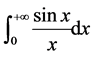 是积分学中著名的积分,许多重要积分的计算最后都化为此积分,本文在
是积分学中著名的积分,许多重要积分的计算最后都化为此积分,本文在
传统的狄利克雷积分证明进行了改进,并在此基础上,将复变函数与积分变换、傅里叶变换相结合,提出了两种新的狄利克雷积分证明的方法,较好的简化了狄利克雷积分证明的复杂度。
基金项目
国家自然科学基金(11201354)。