1. 引言
大豆油是我国第一大植物油消费品种,近年来,大豆油的年消费量已经达到1600余万吨,大豆油价格的波动会极大地影响市场的稳定。豆油期货价格的变化在很大程度上反映了未来一段时间豆油现货市场的供需情况,对豆油的价格具有一定的引领作用,在一定程度上可以规避价格波动带来的风险。豆油期货价格的预测显得十分必要。豆油期货自2006年在大连商品交易所上市以来,豆油期货市场规模不断扩大,市场活跃度与参与度持续提升,已经成为农产品期货领域不可或缺的部分。
在金融市场领域,豆油期货市场凭借丰富的投资品种,吸引了大量投资者。其持仓量近年来稳步增长,市场资金关注度也持续上升。豆油期货为相关企业提供了套期保值工具,帮助企业有效规避价格风险,稳定生产经营,维护金融市场的稳定运行。
在作者的所知范围内,国内尚没有学者用LSTM与Transformer模型预测豆油期货价格。但用类似的模型做别的领域预测的很多[1]-[11]。如刘洋,黎玉寒和窦宝明应用LSTM模型预测棉花期货价格[10],范俊明,刘洪久和胡彦蓉应用LSTM模型预测大豆期货价格[11]。辛洲扬应用LSTM与Transformer模型预测股价[8]。
通过训练和实践,本文所建的LSTM-Transformer模型对豆油期货价格的预测值与真实的价格相比,样本外预测平均绝对百分比误差(MAPE)为1.9%。能够很好地刻画豆油期货价格的走势与波动。该模型可以为有关部门、豆油生产企业、豆油期货投资者更好把握市场,稳健投资和决策提供一定的理论依据。
2. LSTM-Transformer模型简介
LSTM-Transformer模型是一种融合了长短期记忆网络(Long Short-Term Memory, LSTM)和Transformer架构的深度学习模型。
LSTM是一种特殊的循环神经网络(RNN),其优势在于能够有效处理长序列数据中的长期依赖问题。LSTM通过引入门控机制,包括输入门、遗忘门和输出门,以及细胞状态,实现对信息的选择性记忆与遗忘。输入门决定当前输入信息有多少将被添加到细胞状态中;遗忘门控制着细胞状态中哪些信息需要被保留或丢弃;输出门则根据细胞状态和当前输入来确定输出内容。这种机制使得LSTM可以长时间记住重要信息,避免在处理长序列时出现梯度消失或梯度爆炸的问题。
Transformer是一种基于注意力机制的架构,与传统循环神经网络不同,它不依赖于循环结构来处理序列数据,而是通过多头注意力机制并行地关注输入序列的不同部分,从而更全面地捕捉数据中的复杂特征和长距离依赖关系。多头注意力机制将输入数据通过多个线性变换映射到不同的子空间,每个子空间独立计算注意力权重,然后将多个头的注意力结果进行拼接和线性变换,得到最终输出。这使得Transformer能够从不同角度捕捉数据特征,提高模型的表达能力。
LSTM-Transformer模型结合了LSTM和Transformer的优势。在该模型中,数据首先经过LSTM层进行初步处理。LSTM层利用其门控机制,能够有效地提取时间序列中的长期依赖信息,对数据的长期趋势进行建模。然后,LSTM层的输出被传入Transformer层。Transformer层的多头注意力机制进一步挖掘数据中的复杂特征和全局依赖关系,捕捉数据在不同时间步之间的复杂关联。最后,通过全连接层将模型输出维度调整为所需的预测维度,得到最终的预测结果。
3. 数据选择与处理
3.1. 数据来源
本文研究收集了来自权威金融数据平台(akshare)的豆油期货历史交易数据,涵盖了从2006年1月9日到2024年12月9日的日度交易信息,包括开盘价、最高价、最低价、收盘价、成交量等关键指标。这些数据为后续的模型训练和分析提供了丰富的素材,能够较为全面地反映豆油期货市场的价格走势和交易活跃度。
3.2. 数据清洗
在原始数据中,存在部分缺失值和异常值,这些数据可能会干扰模型的训练和预测效果。对于缺失值,采用了基于时间序列的线性插值法进行填充,即根据缺失值前后的有效数据点,通过线性拟合的方式估算出缺失值。对于异常值,通过设定合理的价格波动范围和成交量阈值进行识别和处理。例如,若某一交易日的价格波动超出了历史平均波动范围的一定倍数,或者成交量与近期平均成交量相比出现异常大幅波动,则将该数据点视为异常值,并根据周边数据的趋势进行修正或删除,以确保数据的质量和可靠性。
3.3. 日期处理
将日期列转换为日期时间类型后,提取年份信息,并以年份作为索引。这有助于在后续的数据分析和模型训练中,更清晰地观察价格在不同年份间的变化趋势,以及发现可能存在的季节性和周期性规律,同时也方便模型在时间维度上进行有效学习和预测。
3.4. 数据归一化
为了使不同规模的数据能够在同一尺度下进行处理,提高模型训练的效率和稳定性,对收盘价进行归一化处理。采用MinMaxScaler将数据映射到[0, 1]区间,其公式为:
xnorm=x−xminxmax−xmin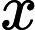
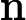

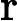
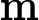

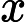

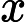
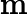
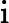
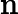
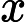
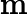
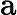
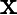

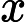
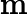
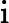
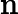
其中x为原始数据,
xmin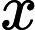
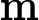
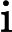
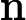 和
xmax
和
xmax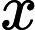
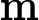
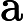
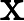 分别为数据集中的最小值和最大值,
xnorm
分别为数据集中的最小值和最大值,
xnorm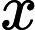
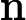

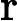
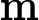 为归一化后的结果。经过归一化处理后,数据的分布更加均匀,有助于模型更快地收敛和提高预测性能。
为归一化后的结果。经过归一化处理后,数据的分布更加均匀,有助于模型更快地收敛和提高预测性能。
4. 模型建立
4.1. LSTM层
LSTM层在模型中起着关键作用,其能够通过独特的门控机制有效处理时间序列中的长期依赖关系。在本研究的模型中,设置LSTM层的输出维度为64,并使其返回序列。LSTM单元内部包含输入门、遗忘门和输出门,其核心计算公式如下:
输入门:
it=σ(Wxixt+Whiht−1+bi)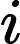


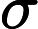
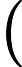
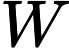
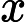

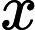


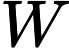
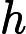

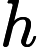




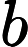


遗忘门:
ft=σ(Wxfxt+Whfht−1+bf)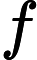


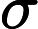
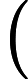
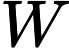
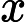
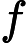
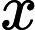


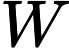
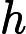
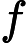
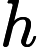




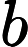
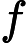
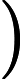
输出门:
ot=σ(Wxoxt+Whoht−1+bo)


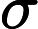
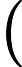
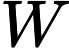
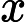

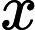


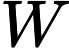
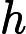

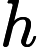




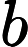


细胞状态更新:
ct=ft⊙ct−1+it⊙tanh(Wxcxt+Whcht−1+bc)


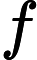







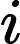


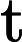
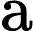
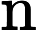
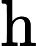
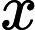


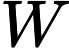
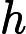
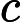
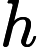




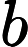
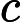

隐藏状态输出:
ht=ot⊙tanh(ct)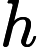





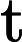
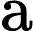
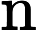
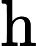



其中,
xt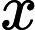
 为当前时刻的输入数据,
ht−1
为当前时刻的输入数据,
ht−1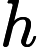


 为上一时刻的隐藏状态,W为权重矩阵,b为偏置向量,
σ
为上一时刻的隐藏状态,W为权重矩阵,b为偏置向量,
σ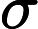 为sigmoid函数,
⊙
为sigmoid函数,
⊙ 表示元素级乘法。通过这些门控机制,LSTM能够有选择地保留或遗忘历史信息,从而更好地捕捉时间序列的长期趋势。
表示元素级乘法。通过这些门控机制,LSTM能够有选择地保留或遗忘历史信息,从而更好地捕捉时间序列的长期趋势。
4.2. Transformer层
Transformer层引入了多头注意力机制(MultiHeadAttention),能够并行地关注输入序列的不同部分,从而更全面地捕捉数据中的复杂特征和依赖关系。在本模型中,设置头数为4,键维度为64。多头注意力机制的计算过程如下:
首先,通过线性变换将输入X分别映射到查询矩阵Q、键矩阵K和值矩阵V,即
Q=WQX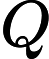

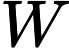
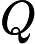
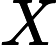 ,
K=WKX
,
K=WKX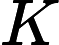

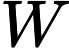
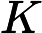
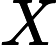 ,
V=WVX
,
V=WVX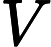

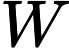
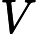
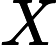 ,其中
WQ
,其中
WQ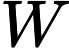
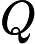 、
WK
、
WK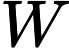
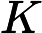 、
WV
、
WV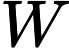
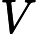 为相应的权重矩阵。
为相应的权重矩阵。
然后,计算注意力权重:
Attention(Q,K,V)=softmax(QKT√dk)V,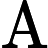
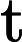
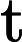

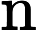
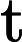
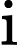

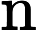
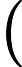
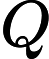
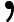
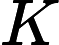
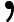
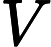


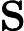

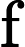
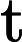
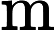
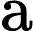
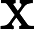
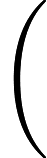
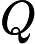
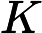
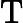
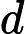
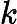
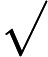
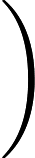
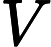
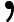
其中
dk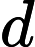
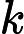 为键维度。最后,将多个头的注意力结果进行拼接并通过线性变换得到最终输出:
为键维度。最后,将多个头的注意力结果进行拼接并通过线性变换得到最终输出:
MultiHeadAttention(Q,K,V)=concat(head1,⋯,headh0)Wo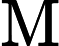
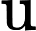
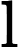
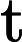
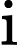


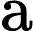
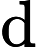
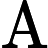
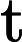
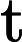

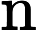
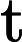
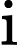

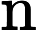
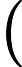
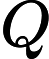
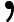
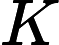
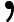
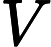


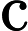

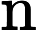
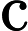
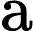
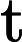
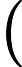
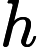
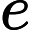
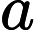
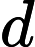

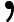
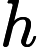
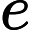
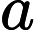
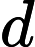
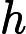
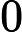

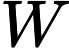
 ,
,
其中
headi=Attention(Qi,Ki,Vi)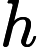
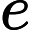
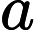
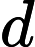


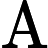
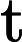
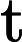

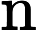
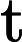
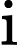

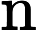
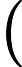
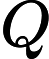

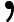
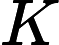

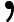
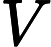

 ,
Wo
,
Wo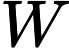
 为输出权重矩阵。
为输出权重矩阵。
在多头注意力机制之后,还经过了Dropout层进行随机失活操作,防止过拟合,其计算公式为
y={0,if p<dropout ratex1−dropout rate,otherwise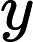

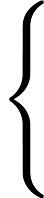
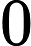
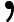
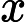


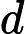
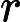

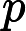

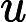


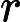
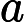

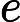
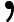
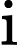
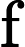

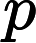

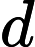
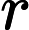

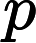

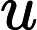
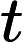

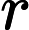
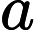
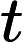
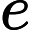

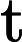
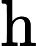

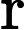
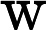
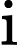
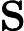
 ,
,
其中x为输入,y为输出,p为随机生成的概率值。接着通过层归一化(LayerNormalization)将输入归一化到均值为 0、方差为1的分布,公式为
LayerNorm(x)=x−μ√σ2−ε,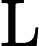
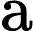
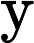

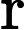


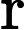
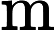
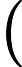
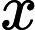


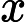

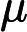
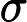
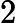

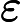
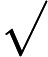
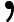
其中
μ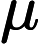 为均值,
σ
为均值,
σ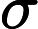 为标准差,
ε
为标准差,
ε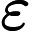 为防止除零的小常数。随后,通过全连接(Dense)和ReLU激活函数进一步提取特征,ReLU函数公式为
ReLU(x)=max(0,x)
为防止除零的小常数。随后,通过全连接(Dense)和ReLU激活函数进一步提取特征,ReLU函数公式为
ReLU(x)=max(0,x)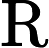

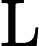

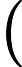
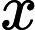


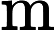
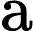
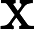
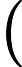
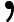
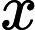
 。同样,经过Dropout和层归一化处理,增强模型的泛化能力。
。同样,经过Dropout和层归一化处理,增强模型的泛化能力。
4.3. 模型构建
将LSTM层和Transformer层组合构建完整的LSTM-Transformer模型。输入数据首先经过LSTM层进行初步处理,提取时间序列中的长期依赖信息,然后将LSTM层的输出传入Transformer层,利用多头注意力机制进一步挖掘数据中的复杂特征和全局依赖关系。最后,通过一个全连接层将模型输出维度调整为1,得到最终的预测价格。在模型编译过程中,选择Adam优化器,其通过自适应调整学习率来优化模型参数,计算公式为:
mt=β1mt−1+(1−β1)gt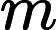


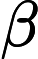

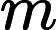




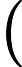


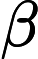


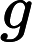

vt=β2vt−1+(1−β2)g2t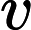


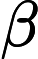
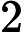
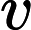




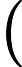


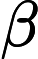
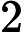

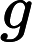
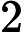

ˆmt=mt1−βt1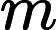
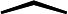


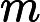
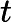


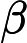
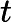
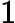
ˆvt=vt1−βt2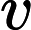
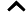


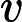
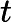


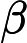
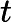
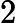
θt+1=θt−αˆmt√ˆvt+ε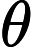

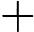


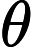


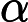
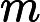
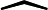
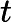
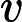
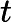
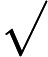
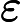
其中,
mt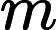
 和
vt
和
vt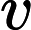
 分别是一阶矩和二阶矩的估计值,
β1
分别是一阶矩和二阶矩的估计值,
β1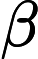
 和
β2
和
β2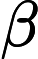
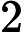 是衰减率,
gt
是衰减率,
gt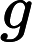
 是梯度,
α
是梯度,
α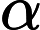 是学习率,
ε
是学习率,
ε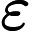 是防止除零的小常数。损失函数采用均方误差(mean_squared_error),其公式为
是防止除零的小常数。损失函数采用均方误差(mean_squared_error),其公式为
MSE=1nn∑i=1(yi−ˆyi)2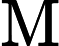
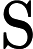
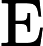


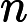




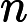
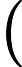
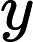


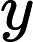


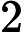
其中
yi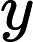
 为真实值,
ˆyi
为真实值,
ˆyi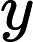
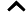
 为预测值,n为样本数量。通过最小化均方误差,使模型预测值尽可能接近真实值。
为预测值,n为样本数量。通过最小化均方误差,使模型预测值尽可能接近真实值。
5. 模型检验
5.1. 划分数据集
将预处理后的数据按照8:2的比例划分为训练集(2006年1月9日~2021年2月26日)和测试集(2021年2月27日~2024年12月9日)。训练集用于模型参数的学习和调整,模型在训练集上不断迭代优化,以拟合数据中的规律和特征。测试集则用于评估模型在未见过数据上的性能,确保模型具有良好的泛化能力,能够准确预测未知数据的价格走势。
5.2. 模型训练
在模型训练过程中,设置epochs (纪元)为10,即对整个训练集进行10次完整的迭代训练。在每次迭代中,batch_size (每批量)为32,意味着每次从训练集中随机抽取32个样本进行一次参数更新。在训练过程中,密切监测训练集和测试集的损失值以及评估指标的变化情况,随着epoch的增加,训练集损失和验证集损失均呈现逐渐下降的趋势,表明模型在不断学习数据中的模式并优化参数。
在模拟训练中,本文对不同的测试集进行了测试,实验表明该模型具有良好的鲁棒性,因为篇幅关系,本文只列出一个测试集的预测结果。
5.3. 评估指标
采用均方根误差(RMSE),平均绝对误差(MAE),平均绝对百分比误差(MAPE)以及相对均方根误差(RRMSE)作为评估模型预测性能的指标。
RMSE能反映预测值与真实值之间的偏差程度,对较大误差更为敏感,其计算公式为
RMSE=√1nn∑i=1(yi−ˆyi)2.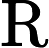
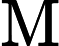
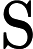
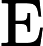






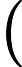
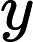


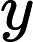















MAE则衡量预测值与真实值的平均绝对偏差,计算公式为
MAE=1nn∑i=1|yi−ˆyi|.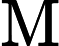
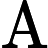
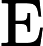


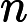




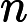
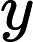


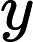

MAPE是衡量预测值与实际值之间绝对百分比误差的平均值,其计算公式为
MAPE=1nn∑i=1|yi−ˆyiyi|×100%.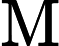
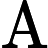
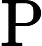
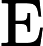


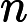




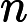
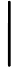
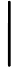
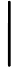
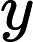


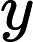

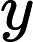



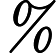
RRMSE是用于衡量观测值与预测值之间差异的统计量,其计算公式为
RRMSE=RMSEˉy=√n∑i=1(yi−ˆyi)2nˉy.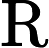
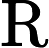
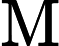
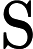
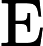

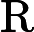
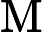
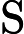
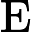
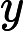



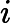

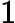
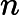
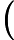
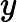
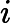

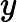

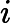
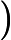
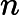



通过这四个指标的综合评估,可以全面了解模型在不同误差尺度上的表现,从而更准确地判断模型的预测精度和稳定性。计算得到训练集的RMSE为155.19,MAE为116.02,MAPE为1.51%,RRMSE为0.022;测试集的RMSE为200.35,MAE为157.16,MAPE为1.90%,RRMSE为0.026。
6. 实验结果与分析
6.1. 预测结果展示
图1展示了LSTM-Transformer模型对价格的预测结果,包括实际价格(蓝色)、训练集预测价格(橙色)和测试集预测价格(绿色)。
Figure 1. Comparison diagram of the prediction results of the training set and the test set with the real data
图1. 训练集、测试集的预测结果与真实数据比较图
对预测结果的分析:
模型对趋势的捕捉能力:从图中可以看出,训练集预测价格和实际价格在大部分时间序列上走势较为贴近,说明模型在训练数据上能够较好地学习价格的波动趋势。测试集预测价格也在一定程度上跟随了实际价格的主要波动,如几个明显的价格峰值和谷值都有体现,表明模型具备一定的泛化能力来捕捉价格波动趋势。
影响较大的特征:LSTM (长短期记忆网络)擅长处理时间序列数据,能够捕捉价格随时间变化的长期依赖关系,比如价格在较长时间段内的上升或下降趋势。而Transformer模型中的自注意力机制,可以让模型在处理序列数据时,关注不同时间点价格之间的关联程度,对价格波动中的关键转折点等特征更为敏感。两者结合,使得模型能够综合考虑价格的历史趋势和不同时间点之间的相互关系,这些时间序列特征和序列内部的关联特征对预测结果影响较大。
预测的偏差:在一些局部区域,训练集预测价格和实际价格之间存在一定偏差,测试集预测价格与实际价格的偏差更为明显,这可能是由于市场中的一些突发因素、异常波动或模型未能完全学习到的复杂模式导致的。
经过训练的模型对训练集和测试集进行预测,并将预测结果进行反归一化处理,使其恢复到原始价格尺度。如图1所示为实际价格(Actual)、训练集预测价格(Train Predict)和测试集预测价格(Test Predict)的变化趋势。从图中可以清晰地看到,训练集预测价格(橙色线)与实际价格(蓝色线)在大部分时间点上较为接近,表明模型在训练集上具有较好的拟合能力。同时,测试集预测价格(绿色线)也能够大致捕捉到实际价格的波动趋势,虽然存在一定的偏差,但整体上显示了模型在未见过的数据上具有一定的预测性能。
6.2. 评估指标分析
LSTM单模型:
训练集表现:MAE为110.82,RMSE为160.54,MAPE为1.87%,RRMSE为0.031。这表明在训练集上,模型预测值与真实值的平均绝对差距为110.82,误差的平方均值的平方根为160.54,平均绝对百分比误差为1.87%,相对均方根误差为0.031,整体训练效果相对较好。
测试集表现:MAE为165.42,RMSE为221.53,MAPE为2.34%,RRMSE为0.026。测试集的各项误差指标均高于训练集,特别是MAE和RMSE提升明显,说明模型存在一定程度的过拟合,在新数据上的泛化能力较弱。
Table 1. Comparison of prediction error indicators
表1. 预测误差指标比较
Model |
MAE |
RMSE |
MAPE |
RRMSE |
LSTM-Training |
110.82 |
160.54 |
1.87% |
0.031 |
LSTM-Testing |
165.42 |
221.53 |
2.34% |
0.026 |
Transformer-Training |
323.73 |
365.45 |
4.55% |
0.051 |
Transformer-Testing |
293.4 |
360.58 |
3.26% |
0.041 |
LSTM-Transformer-Training |
116.02 |
155.19 |
1.51% |
0.022 |
LSTM-Transformer-Testing |
157.16 |
200.35 |
1.90% |
0.026 |
Transformer单模型
LSTM-Transformer模型
训练集表现:MAE为116.02,RMSE为155.19,MAPE为1.51%,RRMSE为0.022。训练集上的各项指标表现良好,尤其是MAPE和RRMSE在三个模型的训练集中最低,说明预测的相对准确性和相对误差控制较好。
测试集表现:MAE为157.16,RMSE为200.35,MAPE为1.90%,RRMSE为0.026。在三种模型的测试集中,该模型的MAE、RMSE、MAPE都是最低的,RRMSE与LSTM单模型测试集相同,表明该组合模型在预测准确性和泛化能力上表现更优,能较好地处理训练集和测试集数据。
7. 结论
本研究成功构建并应用LSTM-Transformer模型对豆油期货价格进行预测。通过严谨的数据处理、合理的模型架构设计以及系统的训练与评估,模型在预测精度上取得了较好的效果,相比单一模型具有明显优势(见表1)。然而,期货市场复杂多变,仍有一些因素可能影响模型的性能。未来研究可以进一步探索结合更多的市场因素和外部数据,如宏观的经济指标、特定时期的天气数据、有影响的政策等,以丰富模型的输入信息,提高模型的预测能力。同时,可以尝试优化模型结构和参数,如调整LSTM层和Transformer层的超参数,引入更先进的训练算法和正则化技术,进一步提升模型在复杂时间序列预测中的性能,为期货市场参与者提供更精准、更可靠的决策支持工具,推动期货市场预测技术的发展。基于时间和篇幅所限,本模型没有考虑宏观经济政策、国际市场行情等特征指标,后续研究可以考虑加入这些有影响的特征指标,以利于提高预测精度。
基金项目
上海工程技术大学大学生创新项目:豆油价格预测(项目编号:cx2421003)。