1. 引言
跳频信号是典型的非平稳信号,其频谱随时间快速变化,具有时间上断续性和每跳间连续性的特点,这就决定了跳频通信具有较强的抗干扰、抗截获能力,从而在军事和民用通信中得到广泛应用 [1] 。因此对于跳频信号的监测和参数估计具有重要意义。
目前时频分析是对诸如跳频信号等非平稳信号进行分析的一种有效工具,常用处理方法包括小波变换 [2] 、短时傅立叶变换 [3] [4] (STFT, Short-Time Fourier Transform)等,小波变换方法需要一定的先验知识条件,且对噪声敏感性很强,当信噪比较低时检测结果准确性较差,STFT方法无需任何先验知识,具有较好的实时性和时频分辨率而得到广泛应用,基于STFT改进的跳频信号参数估计方法层出不穷 [5] [6] [7] [8] [9] ,同步压缩变换法、能量时频对消法、时频矩门限判别法、加权阈值判别法等不断提出,解决了低信噪比情况下信号参数估计的精度问题,但在实际工程应用资源有限且需要兼顾速度和精度指标要求情况下,也存在计算复杂、实时性欠缺和干扰误差较大的情况。
随着大数据和人工智能的快速发展,也提出了基于机器学习和深度学习的监测方法 [10] [11] ,通过采集大量样本数据利用机器学习训练模型或深度神经网络模型对跳频信号进行建模和信号特征估计,该方法具有较高的检测精度,但需要较高的资源成本和较长的学习周期。
本文结合实际工程应用中资源有限条件下满足速度和精度指标的要求,兼顾考虑时频分辨率的矛盾特性,提出了一种基于STFT和时间相关聚类统计分析的跳频参数估计方法。通过对原始IQ数据进行STFT时频分析,得到频率随时间的变化规律,根据跳频信号的频谱特征从二维时频图中提取跳频信号的频谱成分,对跳频信号特征参数进行时间相关聚类统计,并以信号持续时间作为特征统计量,筛除持续时间过长和过短的频点,将其视为定频干扰和突发干扰,降低了运算时间开销和干扰误差,最终根据聚类统计结果采用差分统计直方图方法估算出跳频参数。
2. STFT时频分析
信号时频分析处理最常用的是短时傅立叶变换,其理论基础是假定信号在局部时间窗内为平稳信号,表示信号的时间–频率能量分布,它是对时域信号加窗之后的傅里叶变换。
假设接收到的信号为
,则其STFT定义如式(1)所示。
(1)
其中
为滑动窗函数,其宽度决定了时间分辨率的大小。信号
在t时刻的频谱通过
与滑动窗
相乘获得,是当前分析时刻附近的“局部谱”,能够反映以时间t为中心的滑动窗间隔内所有信号特征。
谱图定义为STFT模值的平方,在二维时频上满足边缘分布特性,对信号瞬时频率和群时延估计存在偏差,并且根据海森伯格不确定性原理,时频分辨率是一对矛盾体。若时间窗取得过长,其频率分辨率提高,但时间分辨率变差,且信号在局部时间窗内平稳的假设也无法成立;若时间窗取得过短,其时间分辨率提高,但频率分辨率变差 [12] 。因此STFT方法采用同一分辨率(即统一窗函数)对跳频信号进行处理,很难满足对高速跳频信号的检测。
从信号处理实时性和设计实现复杂度考虑,跳频信号在某一时刻是窄带信号,但从长时间来看跳频信号在整个频带内跳变是宽带信号,其在整个跳频带宽范围内均匀分布,因此在实际应用中,时间分辨率和频率分辨率采取折中处理,STFT能够满足对于高速跳频信号的处理。
由于STFT具有计算复杂度低、精确度适中、实时性高等特点,因此在跳频信号监测中得到广泛应用。
3. 基本原理和设计实现
基于STFT的跳频参数估计方法的工作原理为:首先通过STFT对原始采样信号进行时频分析处理,获取跳频信号的全域时频矩阵,通过峰值信号法寻找频谱峰值并将峰值点频率作为跳频频点估计值提取其信号特征参数,继而对提取到的信号根据其信号特征进行时间相关聚类统计分析,最终估算出跳频参数信息。
流程如图1所示。
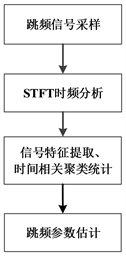
Figure 1. Flowchart of frequency-hopping signal parameter estimation method based on STFT
图1. 基于STFT的跳频参数估计方法流程图
具体步骤如下:
1) 对采样时刻的跳频信号进行STFT时频分析处理,得到反映信号频率随时间变化的二维时频图,即时频矩阵,该时频矩阵由每个滑动窗时段的一维频谱组成。
本方法采用常见的Blackman窗作为滑动窗函数,且滑动过程窗口无交叠,随着时间值的增大,逐步完成信号的分段FFT处理。假定滑动窗口宽度为N,窗口每滑动一次得到N点的FFT结果,并将其按顺序存为时频矩阵的一列,作为跳频信号处理单元,即为滑动窗时段的一维频谱。
2) 确立频谱阈值提取时频矩阵中跳频频点信号,记录其特征参数并进行时间相关聚类统计分析。
时间相关聚类统计分析是利用跳频信号在时间上的断续性和每跳间的连续性等特点,利用获取得到的信号相关特征参数建立信号时频相关特性数组字典(包括信号频率、信号出现次数、信号出现时间、信号持续时间等要素信息,其中信号出现时间和信号持续时间作为信号出现次数的嵌套要素数组,用来记录同一频点在不同时刻出现情况),通过聚类统计分析实现对跳频信号的分类判别,具体流程如下:
a) 预先建立信号相关特性数组,用于存放跳频频点信号特征参数;
b) 根据峰值信号法寻找频谱峰值将其作为频谱阈值,提取时频矩阵中每列频谱峰值点频率,将其作为跳频频点估计值,记录其信号相关特征参数(包括频率、功率、出现时间、持续时间等);
c) 将当前列跳频频点特征参数与前一列提取的跳频频点信号进行逐一聚类统计,对于频率值相同或相近的视为同一频点,并累计记录信号出现时间、持续时间、起跳时间等参数信息,未找到相近频点的视为新频点;
d) 最终处理结束得到每一跳频频点所对应的时频相关特性数组元素值。
时间相关聚类统计分析流程如图2所示。
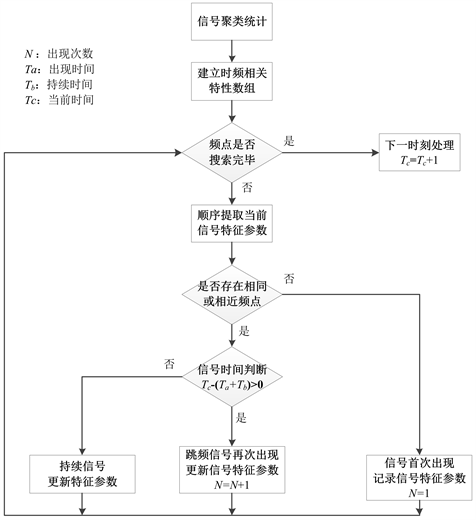
Figure 2. Flowchart of statistical analysis of the time-dependent clusters
图2. 时间相关聚类统计分析流程图
3) 依据时间相关聚类统计结果进行跳频参数估计,包括驻留时间、跳频周期、跳速等参数信息。
跳频参数估计采用时间相关聚类统计方法,并通过均值处理降低估计误差。该方法首先将时频相关特性数组按信号出现时间的先后进行排序,然后选择不同基准特征量的信号,对跳频信号进行检测估计。
针对单跳频电台,由于其跳速是固定的,因此可将频点的持续时间作为特征统计量,并对信号时频相关特性数组进行筛除处理,筛除持续时间过长和过短的频点,将其视为定频干扰和突发干扰。
假设聚类统计结果中信号持续时间出现概率最大的为
,STFT时间窗长为
,则认为时频特性相关数组内信号持续时间满足
范围条件的信号为跳频信号频点,其信号持续时间
估计为
(2)
式中
、
、
分别为对应持续时间的统计个数。
跳频周期由持续时间和起跳时间组成,对时频特性相关数组中的起跳时间按照时间顺序进行差分运算,统计差分值中相同差值数目,假设差值出现概率最高的为
,则跳频周期
估计为
(3)
式中
、
、
为三个相邻差值个数。
跳速
由下式求得:
(4)
根据跳频信号出现的规律,上一跳起始时间加上持续时间等于下一跳的起始时间及信号持续时间等参数统计信息,在时频相关特性数组提取频率集信息。
4. 结果仿真
在仿真实验中,用Matlab产生模拟的跳频信号。跳频频率范围80 MHz (零中频),频点间隔100 kHz,跳速1000 hop/s。
STFT时频分析得到三维时频图,如图3所示。

Figure 3. Three dimensional time-frequency diagram
图3. 三维时频图
俯视得到二维时频图,如图4所示。

Figure 4. Two dimensional time-frequency diagram
图4. 二维时频图
检测到的跳频集图案如图5所示。
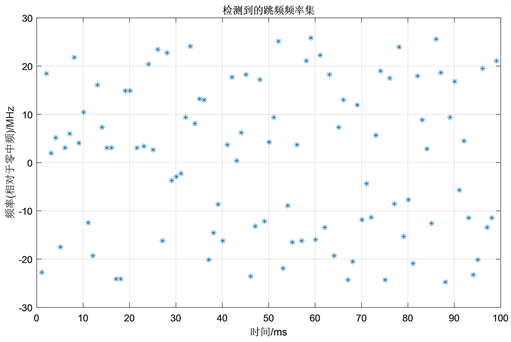
Figure 5. Frequency-hopping collection diagram
图5. 跳频集图案
依据时间相关聚类统计结果对跳频信号时频特性相关数组中的起跳时间按照时间顺序进行差分运算,起跳时间差统计如图6所示。

Figure 6. The histogram of time difference of hopping
图6. 起跳时间差统计直方图
图中显示时间差为1 ms的个体数最多,由上述公式(3)计算得出跳频周期约为1 ms,跳速
hop/s,跳频集由聚类统计结果的时频相关特性数组获得。
5. 结论
针对跳频信号的非平稳性和频率时变性,本文采用STFT时域分析处理提取信号特征参数并进行时间相关聚类统计分析,以特征参数统计方法代替复杂估计算法降低了运算时间开销,同时以信号持续时间为特征量的统计筛选更有效避免定频和突发干扰,降低了干扰误差,最终依据统计分析结果给出跳频参数估计。仿真结果表明,该方法能够有效实现对跳频信号的检测和特征参数估计。