1. 引言
齿轮传动具有传动平稳、工作可靠、使用寿命长、适用范围广,传递效率高等特点,被广泛地应用于各种机械产品和设备中 [1] 。齿轮传动过程中由于轮齿之间交替接触、啮合点位置和齿间载荷分配不断改变等原因,齿轮啮合瞬间发生应力变化。因此,研究齿轮啮合及有限元分析对于提高齿轮设计和优化水平、减少实验和成本、提高安全性和可靠性等方面具有重要意义。
国内外学者对齿轮啮合方面做了大量研究。胡建成 [2] 等人对直齿圆柱齿轮传动系统进行了公差规范和分析,改进了雅可比旋量模型,引入齿轮侧隙,建立了综合、合理、有效的装配体公差设计模型。Chen Hua [3] 等提出了一种新的齿轮公差分析方法,通过研究模量偏差和压力角偏差的影响。郭恒 [4] 等基于有限元建立了齿轮温度场和传动误差模型,为齿轮传动性能分析提供了依据。张磊 [5] 等研究了含有齿廓总偏差的齿轮模型建立方法。钱露露 [6] 等采用节点法建立了三维有限元模态分析模型,实现了齿轮实验减振避振。邱林 [7] 等对渐开线弧齿圆柱齿轮进行了模态分析,为齿轮优化提供了参考依据。王彦军 [8] 等通过有限元导入进行了模态分析,为动态分析提供依据。刘荫荫 [9] 等利用有限元对齿轮传动系统进行了模态分析,验证了设计的准确性。Agrawal Anant Prakash [10] 等对齿轮在循环载荷作用下进行了有限元分析,优化了齿轮设计,提高了寿命。王红香 [11] 等基于接触赫兹理论进行了接触应力分析。林支慨 [12] 等基于有限元法对圆柱接触和齿轮接触进行了静力学分析,提高了分析精度。Shashi Kumar G [13] 等进行了斜齿轮的数值分析,验证了设计的合理性。周海燕 [14] 等通过动力学接触分析改进了齿轮接触载荷分布。邱水才 [15] 等利用KISSsoft建立了齿轮副模型,提高了传动性能。
本文以某二级减速器中标准直齿圆柱齿轮啮合为研究对象,研究不同网格划分对齿轮啮合分析的影响。采用ANSYS Workbench对齿轮进行了模态分析,对齿轮啮合进行瞬态结构分析,并采用赫兹理论进行齿面接触应力计算对比,从而为齿轮传动动态设计提供依据。
2. 齿轮建模与网格划分
齿轮材料参数和基本几何参数分别如表1、表2所示。以表1中参数为依据,在SolidWorks中用方程式驱动绘制每个轮齿齿廓,建立齿厚为10 mm的齿轮三维模型。装配使之啮合传动。将模型导入Workbench中,建立相应模态分析和瞬态结构模块,设定工程数据源中的材料,对两个啮合齿轮进行材料赋值,选用结构钢为分析目标材料。外部载荷设定时,模拟的是齿轮啮合过程中轮齿之间接触的变化。分别采用四面体网格划分和多区域网格划分,对啮合区域再细化划分网格,如图1。
3. 模态分析
3.1. 模态理论
模拟分析可以确定结构的自振周期和结构特性,从而制定合理的瞬态分析时间步长。有利于提高瞬态分析的准确性。

Table 1. Basic geometry of gears
表1. 齿轮基本几何参数
在模态分析中,无阻尼模态分析是经典的特征值问题,此时的运动方程为:
(1)
其对应的特征方程为:
(2)
式中:
是质量矩阵;
是刚度矩阵;
是位移矢量;
是速度矢量;
是加速度矢量。方程的特征值为
。将模型材料弹性模量、泊松比、密度等定义好,才能精确求解。模态求解图示例如图2、图3。
3.2. 具体分析
将模型导入模态分析中,通过分析其每个单一齿轮模态,得到其固有频率和振型。设置分析齿轮材料为结构钢,小齿轮网格划分为1 mm,16,590个单元,77,257个节点,大齿轮网格划分为1 mm,36,570个单元,165,571个节点。对相应的齿轮轴施加固定约束。提取前10阶模态,求解其固有频率。大小齿轮前10阶频率如下表3、表4。

Table 3. The natural frequency of the first 10 steps of the small gear
表3. 小齿轮前10阶的固有频率

Table 4. The natural frequency of the first 10 steps of the large gear
表4. 大齿轮前10阶的固有频率
模态分析可得到不同振型的位移。振型可分为对折振、扭转振、径向振、圆周振、伞形振、弯曲振。通过上表数据横向来看,小齿轮的固有频率明显比大齿轮的固有频率大。纵向来看,小齿轮的第2、3、5、6、7、8、9和10阶的相对位移比较大,并且都表现为对折振。其中第1阶为圆周振,第2、3、7、8阶为一阶对折振,第5、6阶为二阶对折振,第9、10阶为三阶对折振,第4阶为伞形振。大齿轮的各阶振型与小齿轮振型一致。由此可以得出对折振对齿轮传动的影响较大,在传动中应该避免此类振型对齿轮的影响,见下图4~7。对振动影响较大的主要是低阶的模态。
通过振型图可以直观地分析齿轮传动的动态特性,找出齿轮的薄弱环节。作为对照,将赋值材料为灰铸铁,网格划分和结构钢一致,发现灰铸铁的各阶频率较结构钢低,但振型与上述一致。说明材料相差不大的情况下,齿轮的振型变化没有显著影响,进行后续的瞬态动力学分析。
 (a)
(a) (b)
(b)
Figure 4. The first mode of large and small gears
图4. 大、小齿轮第1阶模态
 (a)
(a)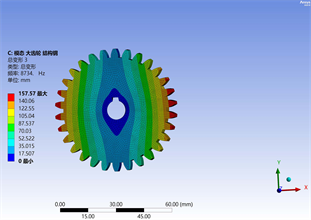 (b)
(b)
Figure 5. 3th mode of large and small gears
图5. 大、小齿轮第3阶模态
 (a)
(a) (b)
(b)
Figure 6. 6th mode of large and small gears
图6. 大、小齿轮第6阶模态
 (a)
(a) (b)
(b)
Figure 7. 9th mode of large and small gears
图7. 大、小齿轮第9阶模态
4. 基于赫兹理论的齿面强度理论计算
齿轮啮合时,轮齿在靠近节线处的相对滑动速度较低,润滑不良,摩擦力较大,易出现点蚀,所以需要考虑此处理论上的应力强度。外齿轮齿面最大接触应力可以用赫兹理论公式来计算,公式相关参数如下:
(3)
式中:
为接触应力;
为法向力,
;
、
两齿廓在节点处的曲率半径;
、
为泊松比;
、
为两齿轮的弹性模量;
为接触线长度,
;
为端面重合度。
取上述例子中齿轮厚度
mm,
N为例,经查标准外啮合圆柱齿轮的端面重合度表计算 [1] ,
,接触线长度
mm,将
MPa,代入式(3),经计算得出接触应力大小为:
MPa。
5. 齿轮啮合瞬态动力学分析
5.1. 动力学理论
由经典力学理论可知,物体的动力学通用方程为:
(4)
式中,
是质量矩阵;
是阻尼矩阵;
是刚度矩阵;
是位移矢量;
是力矢量;
是速度矢量;
是加速度矢量。
在齿轮啮合中,通过瞬态动力学分析结果,可模拟出位移、应力节点云图,从中可以非常直观的看到在载荷的作用下,位移变形情况及最大的位移变形量、齿轮各部位所受应力状态分布以及所受最大的应力等情况,预测齿轮的动态性能,避免冲击、不稳定的运动,为热分析、疲劳分析等分析提供基础。
5.2. 具体分析
将大小齿轮的材料设置为结构钢。将小齿轮齿廓面设置为接触面,将大齿轮齿廓设置为目标面。划分齿面,对轮齿受力部分进行细化网格。分别采用四面体网格划分和多区域网格划分2种方式对齿轮进行网格划分,进行分析比较。细化啮合轮齿部分都划分成1 mm网格,分别为四面体节点65,811个,单元数36,450个和多区域节点225,653个,单元48,930个。如图8、图9。
接触方式为摩擦,选择0.15的摩擦系数,法向刚度因数为0.01。分析设置计算总时长为1 s,设置初始子步为25,最小子步为20,最大子步为250。对小齿轮施加360˚的旋转副,对大齿轮施加一个1000 N的扭矩。
5.3. 瞬态动力学后处理与分析
通过对直齿轮副进行瞬态动力学分析求解,得出其在不同状况下的总变形图和等效应力图,如图10~12。

Figure 11. Equivalent stress diagram for tetrahedral mesh division
图11. 四面体网格划分等效应力图
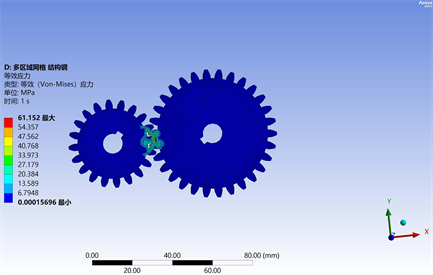
Figure 12. Equivalent stress diagram for multi region grid division
图12. 多区域网格划分等效应力图
根据图11、图12的分析及统计结果,可发现:
1) 四面体网格单元和多区域网格单元对分析效率有影响,四面体网格划分单元节点少,分析处理快。多区域网格划分更为细致,分析接触结果均匀,分析时间长,但对模型分析的精确性更高。故宜采用多区域划分进行瞬态动力学分析。
2) 通过对齿轮啮合过程中,最大等效应力值随时间变化的数据进行统计后,得出结论。主动轮与从动轮刚接触啮合的时候,所产生的等效应力最大,应力值波动范围较大。但随着时间的推移,应力值趋向于稳定,这是因为在开始啮合转动过程中,主动轮具有一定的冲击力,导致齿轮啮合产生的等效应力值较大,但随着啮合的稳定进行,齿轮啮合等效应力趋向于稳定。
3) 最大的接触应力出现在轮齿啮合的齿顶的节线处和轮齿中间处(即齿轮啮合瞬间的位置),如图13。齿轮啮合发生点蚀,应力集中于此并向四周逐渐减小。
文中第3节采用赫兹理论计算出的最大接触应力理论数值为61.168 MPa,而采用四面体网格划分仿真得出的最大接触应力为52.241 MPa (图11),多区域网格划分仿真计算出的最大接触应力为61.152 MPa (图13)。这三者比较,采用四面体网格划分仿真得出最大接触应力与理论计算值相差较大,而多区域网格划分仿真得出的最大接触应力更接近理论计算值。
6. 结语
本文以某二级减速器中标准直齿齿轮啮合部分为案例,采用有限元分析方法进行了深入探究。主要包括以下几个方面:1) 进行了模态分析,确定了齿轮在不同频率下的振动模式和振型图。2) 通过对齿轮啮合的瞬态结构进行分析,发现了应力主要集中的区域,并评估了齿轮的变形程度。3) 将有限元分析结果与赫兹公式计算的理论接触应力值进行了对比,发现在多区域网格划分下,仿真得出的最大接触应力更接近理论计算值。研究结果为后续的齿轮啮合设计优化提供了重要的参考依依据。
NOTES
*通讯作者。