1. 引言
随着经济快速发展,电网规模逐渐扩大,架空导线越来越多,架空线路舞动问题成为困扰电网供电可靠性的主要原因 [1] 。中压配电线路导线采用三相排列的形式,由于早期线路设计标准低,部分线路设施陈旧,在遇到大风、覆冰等恶劣气候时,导线会发生低频舞动现象,舞动幅度过大可能引起风偏放电、相间碰线、绝缘子与金具破损等故障,严重时会造成导线断裂甚至是杆塔倒塌等事故,影响电网的安全稳定运行 [2] 。架空导线舞动防治方法包括规避舞动区域、改变线路设计、舞动抑制和舞动检测。针对已运行的架空导线的舞动防治方法主要是舞动抑制,主要包括防舞动片和相间间隔棒 [3] 。相间间隔棒安装在相与相之间,使相间导线保持一定距离,有效避免了架空线路在风等外力作用下造成的相间短路故障。在架空线路上应用间隔棒是普遍的趋势,根据不同电压等级的架空导线采取各种不同的间隔棒,可以有效解决架空线舞动跳闸问题 [4] 。
输电线路舞动是非常复杂的流固耦合非线性空气动力学问题,覆冰、风、地形条件、导线参数等都会对其产生影响。目前学者对导线舞动特性的研究已经比较成熟。蔡萌琦等考虑了气动阻尼对覆冰四分裂导线舞动的影响,研究了风速和档距对舞动特性的影响。王琼等利用风洞试验获得了新月形和D形两种典型覆冰导线的气动力参数,并对四分裂导线的临界起舞风速和舞动情况进行计算和仿真。祖国强等从强风与覆冰的角度研究了10kV架空导线的舞动特性。目前舞动防治的研究对象多为高压架空线路,然而中低压架空线路分布广泛,其重要性并不亚于高压架空线路。由于早期中压线路设计标准低,部分线路设施陈旧,在恶劣天气工况下舞动严重,易出现线路跳闸甚至是杆塔倒塌等事故。因此,研究探索中低压架空线路的舞动防治方法具有重要意义。
间隔棒的安装方式和安装位置对舞动的防治非常重要,间隔棒的不同安装、连接方式使得导线出现共舞现象时对塔杆施加的应力也不同,如果应力过大,就会使导线从连接绝缘子上的金具处断裂,有可能会把塔杆也一起拉倒。因此,亟待对不同的电压等级的架空导线采取各种不同的间隔棒,对间隔棒的安装方式和安装位置进行优化,降低舞动导致的线路跳闸率,解决10kV架空裸导线舞动跳闸问题。
2. 10kV架空导线的舞动与受力研究
2.1. 覆冰输电线路模型构建
运用数值仿真软件对架空导线覆冰舞动的过程进行模拟,模型由导线、直线杆、绝缘子组成 [5] 。导线两端通过绝缘子与直线杆相连接,直线塔高10 m,线路档距为80 m,三相导线呈等边三角形排布,相间距离为1 m,导线型号为ZS-JKLYJ-10/240,参考外径26.5 mm。
10kV架空导线多为多股绞合导线,刚度小易扭转,导线覆冰后截面多出现圆形、椭圆形 [6] 。本文主要针对圆形覆冰导线进行研究,采用厚度均匀的圆柱形覆冰导线模型,如图1所示。
2.2. 研究计算方法
对于架空线路的舞动分析计算,既要关注架空线路的舞动位移,又要关注导线和杆塔的受力情况。这是一种求解多介质、复杂边界条件的场域问题,有限元法具有独特的优势。计算方法如下:首先将求解域适当划分,将连续问题转化为离散问题;然后对每一个网格用不同的函数表示,最后通过求解代数方程计算所求问题的近似解。本文采用有限元仿真软件comsol进行计算分析。
(1)
(2)
式(1)为表征质量守恒的连续性方程;式(2)为动量守恒的动量方程。上式中:ρ为流体的密度;t为流动时间;v为流体流速,在x,y,z方向上的分量分别为vx,vy,vz;p是流体微元体上的压强;τij(i, j = x, y, z)为分子粘性作用产生的作用于微元体表面的粘性应力;Fx,Fy,Fz为微元体上的体力。
2.3. 仿真参数设置
架空线为钢芯铝绞线,在模型中可将架空导线的材料设置为铝。间隔棒主要由玻璃纤维增强环氧芯棒和橡胶绝缘套组成,其材料的力学强度主要取决于内部的环氧芯棒,因此将间隔棒的材料统一设置为玻璃纤维增强环氧芯棒。求解域材料设置为空气,并且求解域的空间尺寸一般为待求解模型尺寸的8倍。
架空线路所处空间的空气压强为1 atm,环境温度为20℃,导线、覆冰和间隔棒受到垂直向下的重力载荷以及水平方向的流场风力,将直线杆底面设置为固定约束 [7] 。在不同高度设置不同的风速,模拟风速随着高度的升高而逐渐增大。入风口和出风口设置如图2所示。
2.4. 试验数值模拟结果
建立的覆冰导线数值仿真模型,覆冰导线模型满足与输电线路一致的动力与载荷参数,动力作用下,导线会出现低频舞动,导线舞动的能量主要来源于风。图5为风速25 m/s覆冰厚度4 mm时导线舞动水平方向位移与垂直方向位移随时间的变化曲线。由图3可知,在强风和覆冰状态下,导线舞动轨迹呈现椭圆状,舞动幅度约为1.09 m。
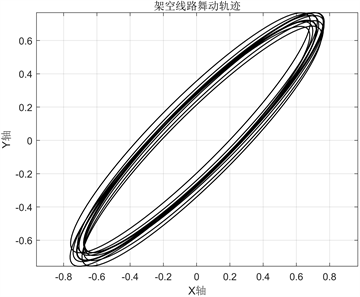
Figure 3. When the wind speed is 25 m/s and the ice thickness is 4 mm, the conductor moves along the path
图3. 风速25 m/s覆冰厚度4 mm时导线舞动轨迹
2.5. 导线在静力和动力作用下的运动状态
模拟覆冰导线在静力和动力状态下对线路和杆塔的影响 [8] 。图4为三相导线在无风无覆冰时导线竖直方向弧垂和无风有4 mm厚度覆冰时导线导线竖直方向弧垂,三相导线产生弧垂后横截面垂坠距离对比图 [9] 。由图4可知,在无风无覆冰的自然悬垂情况下,导线在竖直方向产生弧垂,最大的弧垂为0.9 m。在4 mm的覆冰厚度下,导线竖直方向的弧垂相比于自然悬垂状态大了0.02 m。

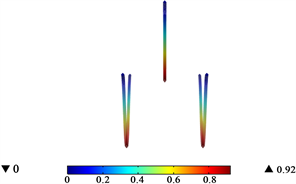 (a) 无覆冰 (b) 覆冰厚度4 mm
(a) 无覆冰 (b) 覆冰厚度4 mm
Figure 4. Static sag of conductor in no wind
图4. 无风时导线静态弧垂
2.6. 覆冰厚度对导线舞动特性的影响
在0~20 mm的覆冰厚度、风速0~40 m/s的范围内进行实验,根据图5显示,导线的舞动幅值随着覆冰厚度的增加呈线性增长的趋势。当覆冰厚度从0 mm增加至20 mm时,导线的舞动幅值可以增加10%至20%。当覆冰厚度不变,风速每增加5 m/s时,导线的舞动幅值增量线性增长,同时,根据图6所示,导线舞动引起的应力变化与幅度变化趋势相同 [10] 。覆冰厚度从0 mm增加至20 mm时,导线所承受的应力可以增加25%至50%,当覆冰厚度不变,风速每增加5 m/s时,导线所承受的应力增量线性增长。由于覆冰增加了线路的重力和迎风面积,因此在覆冰条件下,导线的舞动幅度会略微增加,而覆冰厚度对导线承受应力的影响更为显著。

Figure 5. Conductor galloping amplitude under different ice thickness
图5. 不同覆冰厚度下导线舞动幅值
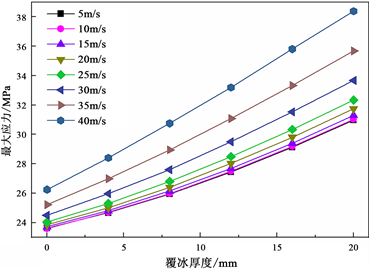
Figure 6. Maximum stress of traverse under different ice thicknesses
图6. 不同覆冰厚度下导线舞动的最大应力
2.7. 导线对舞动特性的影响
在风速25 m/s、风向角90˚的情况下,得到的导线舞动幅值与线径和的关系如图7所示,随着线径的增大,导线舞动幅值先快速减小,后趋于平缓。虽然线径增加会在一定程度上增大导线受到的风力载荷和重力载荷,但其其质量和抗弯能力也会随着线径的增加而增大,惯性越大越不容易偏移,而后者的影响效应更大,因此线径越大导线的舞动幅度越小。导线最大应力与线径的关系如图8所示,导线线径与其受到的应力呈反比关系 [11] 。由此可见,线径越大的导线,其对覆冰舞动的抑制效果越强,在覆冰厚度较大的地区,可以采取适当增大线径的措施从而降低导线舞动的危害 [12] 。

Figure 7. Conductor galloping amplitude under different diameters
图7. 不同线径下导线舞动幅值
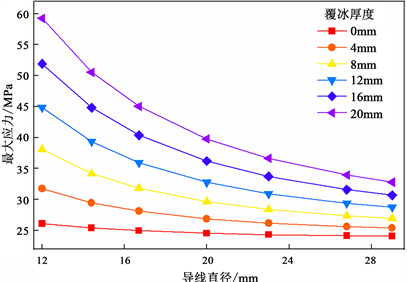
Figure 8. The maximum stress of the conductor under different diameters
图8. 不同线径下导线舞动的最大应力
在相同环境、相同线径情况下,不同导线材质的导线舞动幅值与最大应力如图9和10所示。由图可知,在相同条件下,铜芯导线的舞动幅值是最大的,比铝芯导线的幅度大30%,这主要是由于其密度大,导致其竖直方向受力大、位移大;而铝芯导线受到的应力最小,仅23.8 MPa,这主要是由于其杨氏模量最小。
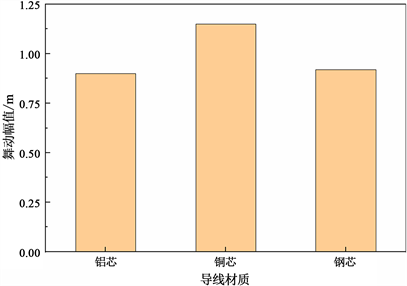
Figure 9. Conductor galloping amplitude under different conductor materials
图9. 不同导线材质下导线舞动幅值
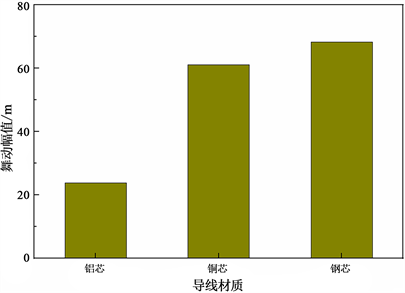
Figure 10. Maximum stress of conductor under different conductor materials
图10. 不同导线材质下导线舞动最大应力
3. 相间间隔棒的选择与安装位置优化
3.1. 间隔棒密度对舞动特性的影响
导线舞动幅值和应力主要取决于材料的密度、模量,为研究间隔棒材质对导线舞动特性的影响,分别改变间隔棒的密度和杨氏模量进行仿真计算,计算不同间隔棒材质下导线舞动位移和应力变化情况 [13] 。仿真结果中,间隔棒的杨氏模量对导线舞动的位移和应力几乎没有影响,因此之考虑不同间隔棒密度对导线舞动特性的影响,结果如图11和图12所示。随着导线密度从1500 kg/m3增大至4000 kg/m3,导线竖直方向偏移和应力会有轻微增大,水平方向偏移没有变化,变化规律和间隔棒覆冰相似。可见,在合理范围内,使用不同材质的间隔棒对导线舞动特性的影响不大。
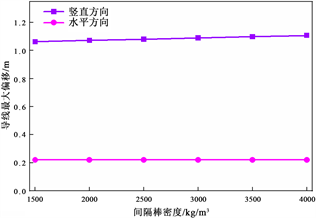
Figure 11. Effect of spacer rod density on traverse migration
图11. 间隔棒密度对导线舞动偏移的影响
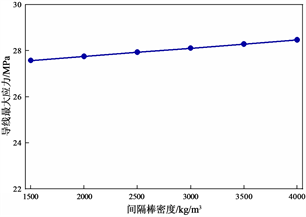
Figure 12. Effect of spacer density on conductor stress
图12. 间隔棒密度对导线应力的影响
3.2. 安装间隔棒后导线耐风能力
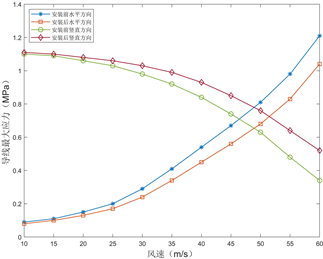
Figure 13. Influence of wind speed on traverse movement deviation after installing spacer bars
图13. 安装间隔棒后风速对导线舞动偏移的影响
为研究安装间隔棒后导线的耐风能力,在导线安装三角形相间间隔棒后,保持其他环境因素、导线、间隔棒等自身条件不变,只改变风速,从10 m/s增大至60 m/s,计算不同风速下导线舞动位移和应力变化情况,结果如图13和图14所示 [14] 。安装相间间隔棒后,不同风速下导线位移和应力的变化规律与不加间隔棒时一致,安装相间间隔棒可以减小导线偏移的幅度,但会略微增大导线受到的应力,但不会造成导线断裂 [15] 。当风速达到60 m/s及以上时,安装间隔棒后导线的水平偏移也超过1 m,因此间隔棒的抗风能力与适用范围为风速小于60 m/s。

Figure 14. Influence of wind speed on stress of wire after installing spacer bars
图14. 安装间隔棒后风速对导线应力的影响
3.3. 间隔棒覆冰后导线耐风能力
如图15、图16和图17所示,间隔棒覆冰对导线耐风能力的影响主要体现在间隔棒覆冰厚度增大时线路的竖直方向偏移和应力会轻微增大,其他影响较小。
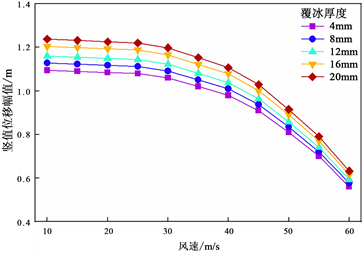
Figure 15. Vertical galloping migration of wires with different spacer ice thickness
图15. 不同间隔棒覆冰厚度时导线的竖直舞动偏移

Figure 16. Horizontal dancing migration of wires with different spacer ice thickness
图16. 不同间隔棒覆冰厚度时导线的水平舞动偏移
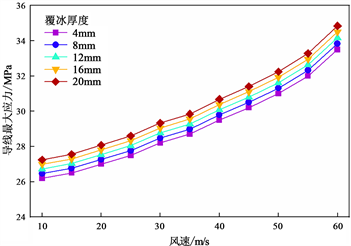
Figure 17. Influence of ice thickness of spacer on stress of conductor
图17. 不同间隔棒覆冰厚度对导线应力的影响
3.4. 间隔棒安装数量与位置
为了进一步研究了间隔棒安装数量对导线舞动的抑制效果,针对整体安装三角形间隔棒的方式,在一个档距内分别等间距地安装1个、2个、和3个间隔棒,三种方案的舞动抑制效果如表1所示。增加间隔棒的安装数量可以提高对导线舞动的抑制效果,除了安装1个间隔棒在1/2档距处会增加导线竖直方向偏移,其他情况都是间隔棒安装数量越多,导线水平和竖直方向的偏移越小,安装3个间隔棒的抑舞效果明显好于安装1个或2个 [16] 。

Table 1. System resulting data of standard experiment
表1. 不同间隔棒安装数量的导线舞动抑制效果
选取在档距1/2、2/3、3/4、4/5处安装一个三角形相间间隔棒,不同安装位置下导线的偏移如图18所示。安装位置越靠近档距中间位置,竖直方向的偏移越大。安装位置靠近导线两端,导线竖直方向的偏移会在档距的3/4处出现极小值,此时导线弧垂最小。

Figure 18. Galloping offset of wires at different installation positions
图18. 不同安装位置下导线的舞动偏移
3.5. 间隔棒端部半导电层作用
对相间间隔棒的电场进行仿真,对比端部有无半导电层对相间间隔棒电场分布影响。图19为相间间隔棒的电场分布云图,半导体边缘已用横线标注。未涂半导电层时,相间间隔棒的电场集中在间隔棒端部,离端部越近场强越高;在端部涂半导电层后,电场最大值偏移至半导电层边缘,端部俩电场距离变大,场强由原来降低40%至50%。可见在间隔棒端部涂抹半导电层有效分散了应力集中与电场集中,可优化电场,起到屏蔽作用。
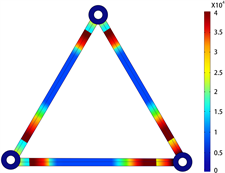
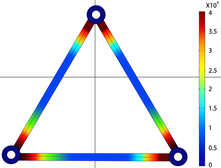 (a) 无半导电层 (b) 有半导电层
(a) 无半导电层 (b) 有半导电层
Figure 19. Effect of semi-conductive layer on electric field distribution of interphase spacer
图19. 半导电层对相间间隔棒电场分布影响
3.6. 间隔棒伞裙的作用
伞裙可以防雨,还可以减小间隔棒表面电场畸变,优化间隔棒的电场分布,增强间隔棒的沿面的绝缘特性,一定程度上增大爬电距离,可以提高间隔棒的防闪络性能。图20为间隔棒电场分布云图。现有间隔棒每根间隔棒只有一个伞裙设置在中间,缺点是间隔棒中间距离两端导线最远,是电场畸变最小的区域。一个间隔棒装设两个伞裙,两个伞裙的位置对称使得间隔棒保持平衡,斜边上的两个伞裙的方向向下,防止雨水积聚。底边上的两个伞裙方向相反使间隔棒呈轴对称图形,在受到风等外力作用时能保持相对平衡。
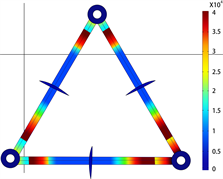
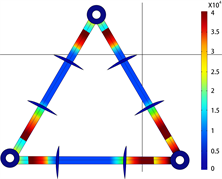 (a) 一伞裙 (b) 两伞裙
(a) 一伞裙 (b) 两伞裙
Figure 20. Effect of the number of parachute skirts on the electric field distribution of interphase spacers
图20. 伞裙数量对相间间隔棒电场分布影响
4. 现场应用验证
使用无人机从水平方向上拍摄架空线安装间隔棒前在竖直方向上的舞动图像,如下图21所示。从图中可以看出竖直方向上舞动幅度最大达160个像素单位,旋转位移角度最大达36˚,由此可以计算得到竖直方向上舞动幅度最大达59 cm。由此可见在风力较大时,该架空线线路舞动幅度可达0.6 m。
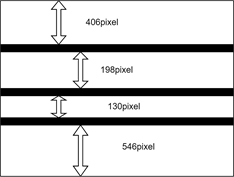 (a) 竖直向下舞动幅度最大时无人机成像
(a) 竖直向下舞动幅度最大时无人机成像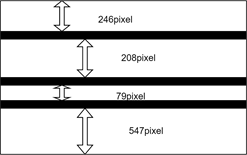 (b) 竖直向上舞动幅度最大时无人机成像
(b) 竖直向上舞动幅度最大时无人机成像
Figure 21. Vertical motion image of overhead line before spacer bar installation
图21. 安装间隔棒前架空线竖直方向舞动图像
使用无人机从水平方向上拍摄架空线安装间隔棒后在竖直方向上的舞动图像,如图22所示。从图中可以看出竖直方向上舞动幅度最大仅有30个像素单位,旋转位移角度最大达28˚,由此可以计算得到竖直方向上舞动幅度最大达31 cm。
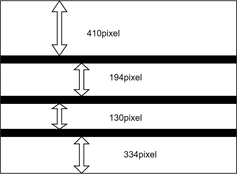 (a) 竖直向下舞动幅度最大时无人机成像
(a) 竖直向下舞动幅度最大时无人机成像 (b) 竖直向上舞动幅度最大时无人机成像
(b) 竖直向上舞动幅度最大时无人机成像
Figure 22. Vertical motion image of overhead line after spacer bar installation
图22. 安装间隔棒后架空线竖直方向舞动图像
5. 结论
本文采用有限元方法模拟分析了三角形排布中压架空线路的覆冰舞动特性,研究了采用相间间隔棒的防舞方案,通过研究野外架空线路的舞动现象,对三角形相间间隔棒进行了优化设计,得出如下结论:
1) 导线舞动幅值和应力与覆冰厚度呈正相关,覆冰厚度对导线受力的影响更大。
2) 舞动幅值和应力与导线线径呈反相关,可以通过增大线径抑制导线舞动,覆冰厚度越大,增大线径获得的抑舞效果越明显。相比于其他材质导线,铝芯导线受到的应力最小,舞动幅值也不大。
3) 增加间隔棒的安装数量可以提升对导线舞动的抑制效果,但也会增加导线承受的负荷和应力,安装时需要综合考虑经济成本和安全效益,选取合适的安装数量。
4) 加装间隔棒可以显著的降低架空线路舞动幅度,间隔棒覆冰厚度和间隔棒的材质对导线舞动特性影响变小;有效的降低架空线路舞动的旋转角度,从而降低垂直位移。