1. 引言
呼吸对于哺乳动物来说至关重要,它关乎到身体的正常运转和生存。研究表明,位于延髓特定区域的前包钦格复合体(pre-Bötzinger complex)是呼吸相关神经元群的集合体,它与呼吸节律的产生和调控密切相关 [1] [2] 。该部位中的神经元会自发产生规律性的簇状发电,并经过中间神经元来指导肌肉控制呼吸 [3] [4] [5] 。为了探究呼吸节律的产生机制,研究者们根据数值模拟和实验观察建立了一系列数学模型,并结合非线性动力学理论广泛研究神经元的放电模式。
经典的Hodgkin-Huxley模型(H-H模型)是一个描述神经元中动作电位如何产生和传导的数学模型,该模型利用细胞内外离子进出细胞的行为详尽地解释了动作电位的产生机制 [6] 。此后,研究者们在H-H模型的基础上提出了不同的关于pre-BötC的呼吸系统计算模型。1999年,Butera等人为pre-BötC中的单个和耦合神经元分别建立基于持续性钠电流(INaP)的数学模型 [7] [8] 。在此基础上,Toporikova和Butera提出了一个具有两种簇放电机制的双室pre-BötC数学模型(TB模型),该模型的胞体簇放电由持续钠电流(INaP)来激活,而树突簇放电依赖于钙激活非特异性阳离子电流(ICAN) [9] [10] 。随后,Park和Rubin在2013年改进并简化了TB模型,建立了pre-BötC神经元单室数学模型,并给出了胞体簇、树突簇和胞体–树突簇的产生机理和影响因素 [11] 。
快慢变量分离和分岔分析两种经典的动力学分析方法,对放电模式的研究起着极其重要的作用 [12] [13] [14] 。在此基础上,Izhikevich从动力学的角度揭示了神经元放电活动的本质特征,并将簇放电进行了归纳和分类 [15] 。近年来,对混合簇放电(MB)的研究逐渐引起学者们的关注。混合簇放电是指在一个周期内包含多种类型簇放电的放电模式 [16] 。Wang和Rubin研究了混合簇放电的产生机制,发现第三维时间尺度对于产生混合簇放电不是必要的 [17] 。Lü等人研究了钠电导(gNa)和钾电导(gK)变化对pre-BötC混合簇放电模式的影响,给出了若干新的混合放电模式,并揭示了这些放电模式的动力学机制 [18] 。Duan等人研究了钾电流对耦合pre-BötC神经元中混合簇放电模式的影响,并研究了混合簇放电的产生及其转迁机制 [19] 。此外,研究者们还对呼吸神经元模型进行了改进。Toporikova和Chevalier等人建立了胚胎期的呼吸神经元模型 [20] 。Wang等人研究了胚胎期呼吸神经元模型随持续钠电导和钙激活的非特异性阳离子电导变化而产生的不同簇放电模式 [21] 。最近的研究也发现KCNQ电流有助于终止新生大鼠内Pre-Bötzinger复合体的吸气簇放电 [22] 。
先前的研究普遍认为混合簇放电依赖于持续钠电流(INaP)和细胞内钙振荡的共同作用,但Lü等研究了一种单纯由钙振荡引起的树突型混合簇放电行为,发现混合簇也可以由树突子系统的钙振荡单独作用产生,并称之为树突型混合簇放电(DMB) [23] 。虽然关于树突型混合簇放电的研究有了一些结果,但在耦合神经元系统中树突型混合簇放电的产生机理值得进一步研究。近期,一些研究聚焦于由两种双慢变量调控的簇放电动力学。Gu等人研究了与疼痛相关神经元的簇放电动力学,其中涉及两个慢变量的调控机制 [24] [25] 。此外,文章 [26] 提出了一种适合分析Wilson模型簇放电的新型双慢变量的快慢变量分离操作流程,这种操作流程适用于两个慢变量都不是特别慢的情况。这些研究为解析簇放电的复杂动力学提供了新的思路。
本文主要研究钙离子动力学参数[IP3]对耦合神经元系统树突型混合簇放电的影响。第二部分介绍了前包钦格复合体的耦合神经元模型;第三部分主要探讨三磷酸肌醇浓度[IP3]的变化对耦合神经元放电模式的影响并解释其产生机制;第四部分给出结论。本文中所有分岔图均由XPPAUT软件画出。
2. 模型介绍
耦合pre-Bötzinger复合体神经元模型的具体描述如下:
(1)
(2)
(3)
(4)
其中
,且
。
代表膜电压,
代表膜电容,
和
分别表示钾离子和钠离子通道的门控变量,
是突触耦合变量。
、
、
、
、
、
分别代表快速钠离子电流、延迟整流钾离子电流、泄露电流、持续钠电流、钙激活非特异性阳离子电流、耦合神经元网络连接所产生的突触电流。模型中各离子电流的表达式如下:
上式中门控电压函数和细胞内钙离子浓度相关的函数表示如下:
钙离子动力学表达式为:
(5)
(6)
其中,
表示细胞内Ca2+浓度,其浓度由从内质网流入细胞质的通量
和从细胞质流出到内质网的通量
决定。
是内质网膜上未被激活的[IP3]通道所占的比例,受
影响。上述表达式中,通量
和
具体形式如下:
(7)
(8)
其中,
和
分别表示内质网的泄漏渗透性和最大可渗透性,
和
分别表示[IP3]和Ca2+所需的[IP3]
受体激活的解离常数。在上式中,
,
是细胞溶质和内质网体积的比率。
公式(1)~(6)称为全系统,公式(1)~(3)称为胞体子系统,公式(5)~(6)称为树突子系统,公式(4)为神经元之间的耦合关系。其中,树突子系统独立于胞体子系统,而胞体子系统受树突子系统影响。系统中其它变量的参数值见附录。
3. 耦合Pre-Bötzinger复合体中的树突型混合簇放电
钙激活非特异性阳离子电流ICAN受细胞内钙离子浓度的调节,而三磷酸肌醇(IP3)则影响着细胞内钙离子的浓度。在一定范围内,随着三磷酸肌醇(IP3)浓度的增加,非特异性阳离子电流ICAN被激活,细胞内钙离子浓度发生周期性波动,从而改变簇放电的类型。通过变化[IP3],可以探讨树突型混合簇放电的动力学机制。
3.1. 三磷酸肌醇浓度对树突型混合簇放电的影响
随着[IP3]的增加,全系统的放电模式从树突型混合簇放电逐渐转变为树突簇放电,如图1(a)所示。膜电位
和细胞内钙离子浓度
随时间t的变化曲线分别由黑色实线和红色虚线表示。分析表明,[IP3]的增加使得全系统的放电周期逐渐减小。图1(b)是极限环的周期随[IP3]的变化规律,显示了极限环的周期随着[IP3]的增加而减小。
为了深入了解树突型混合簇放电的动力学机制,我们将分别对每个树突型混合簇放电的短簇进行动力学分析。在耦合pre-Bötzinger复合体神经元模型中,当初始值相同时,系统表现为同相簇放电;当初始值不同时,系统表现为反相簇放电。本文主要研究同相簇放电。
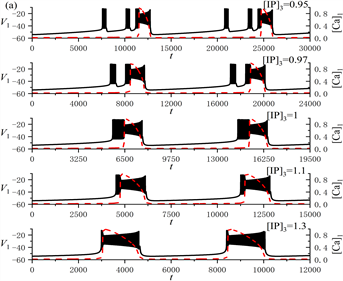
Figure 1. (a) Variation of the dendritic mixed bursting with [IP3]; (b) Change of the period of limit cycle with [IP3]
图1. (a) 树突型混合簇放电的类型随[IP3]的变化情况;(b) 极限环的周期随[IP3]的变化规律
3.2. 树突型混合簇放电的动力学分析
为探究树突型混合簇放电的动力学机制,我们根据
的两个状态将簇放电分为前部和后部,并分别对这两部分进行快慢变量分离和分岔分析。其中,前部对应
缓慢增加的部分,后部对应
突然跳起的部分。对于混合簇放电的前部,取定
为对应短簇的平均值,把
视为慢变量;对于后部,取定
为常数,引入一个新的变量
来替代
,把
视为慢变量。
当[IP3] = 0.95 μM时,全系统的放电模式如图2所示。图中黑色实线代膜电位
的时间序列,红色虚线和橙色实线分别代表细胞内钙离子浓度
和钠通道门控变量
的时间序列,绿色实线代表
随时间
的变化趋势。
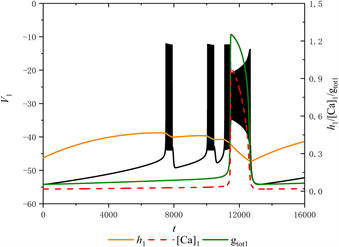
Figure 2. The firing pattern of system with [IP3] = 0.95 μM
图2. [IP3] = 0.95 μM时的放电模式
由于前部的两段短簇类型相同,所以我们只对第一段短簇进行分岔分析。取
,视
为慢变量,对应的单参数分岔如图3(a)所示。图中的F1和F2表示鞍结分岔点,supH表示超临界Hopf分岔点,HC表示同宿轨分岔点,绿色曲线表示全系统的轨线。从图中可以看出,平衡点形成了一条S形曲线,曲线的下支由稳定结点组成,中支由鞍点组成。曲线的上支由稳定和不稳定的焦点组成,不稳定焦点经过超临界Hopf分岔变为稳定焦点,并在超临界Hopf分岔处形成一个稳定的极限环。该稳定极限环的最大振幅值为
,最小振幅值为
,最终通过同宿轨分岔点(HC)后消失。
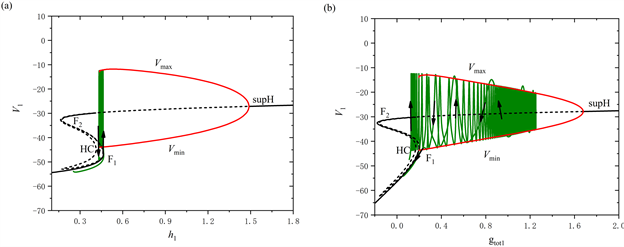
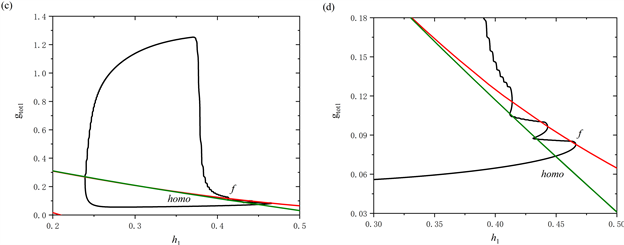
Figure 3. The dynamic analysis with [IP3] = 0.95 μM. (a) One-parameter bifurcation analysis of the first bursting in the first part; (b) One-parameter bifurcation analysis of the bursting in the second part; (c) Two-parameter bifurcation of the trajectory in the (
,
) plane for the mixed bursting; (d) Partial enlargement of (c)
图3. [IP3] = 0.95 μM时的动力学分析。(a) 前部第一段短簇的单参数分岔分析;(b) 后部的单参数分岔分析;(c) 混合簇放电的轨线在(
,
)平面的双参数分岔;(d) 双参数分岔图的局部放大
随着慢变量
的增大,系统的轨线在下支经由鞍结分岔点(F1)跃迁到上支,受稳定极限环的吸引发生振荡,最终经由同宿轨分岔点(HC)落回到下支的静息态。因此,这种簇放电模式为“fold/homoclinic”型簇放电。
对于混合簇放电的后部,取
,选择将
作为慢变量进行分岔分析,如图3(b)所示。系统的轨线在下支经由鞍结分岔点(F1)跳到上支,并随着
的增加不稳定地振荡。由于超临界Hopf分岔(supH)使得稳定极限环产生,轨线受稳定极限环的吸引和不稳定焦点的排斥作用,未能抵达超临界Hopf分岔点(supH),围绕不稳定焦点振荡且振幅逐渐增大,最终经由同宿轨分岔点(HC)返回下支。因此,后部的簇放电模式为经由“fold/homoclinic”滞后环的“Hopf/homoclinic”型簇放电。
树突型混合簇放电的轨线在(
,
)平面的双参数分岔如图3(c)所示,图3(d)为图3(c)的局部放大图。图中包含两条分岔曲线,分别为鞍结分岔曲线(红色实线f)和同宿轨分岔曲线(绿色实线homo),黑色实线为轨线在(
,
)平面上的投影。从图中可以看出,在
缓慢增加的阶段,全系统轨线在鞍结分岔曲线f和同宿轨分岔曲线homo之间来回穿过两次,这表明前部存在两个短簇。随着
突然跳起,后部的短簇出现。
当[IP3]增加至0.97 μM时,全系统的放电模式如图4所示。从图中可以观察到,树突型混合簇放电前部短簇的数量由2个减少至1个。类似于[IP3] = 0.95 μM时的分析过程,通过快慢分解和分岔分析来阐述树突型混合簇放电的产生机制。图5(a),图5(b)分别展示了树突型混合簇放电的前部和后部对应的单参数分岔分析。
对于前部,系统轨线的静息态经由鞍结分岔点(F1)转变为放电态,放电态又经由同宿轨分岔点(HC)转变为静息态,因此前部的簇放电模式为“fold/homoclinic”型簇放电。对于后部,系统的轨线经由鞍结分岔点(F1)跃迁到上支,轨线受到由超临界Hopf分岔产生的稳定极限环的吸引发生振荡,最终放电态经由同宿轨分岔点(HC)转变为静息态,因此后部的簇放电模式为经由“fold/homoclinic”滞后环的“Hopf/homoclinic”型簇放电。
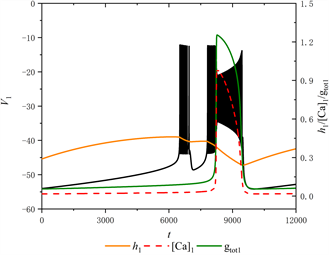
Figure 4. The firing pattern of system with [IP3] = 0.97 μM
图4. [IP3] = 0.97 μM时的放电模式
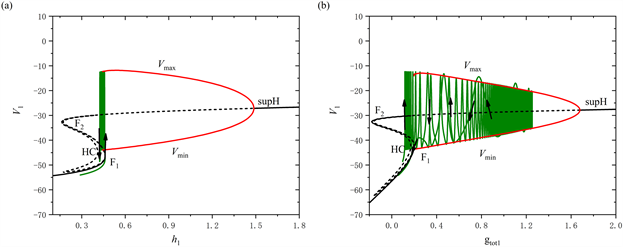
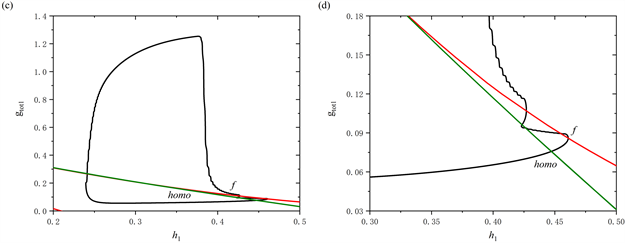
Figure 5. The dynamic analysis with [IP3] = 0.97 μM. (a) One-parameter bifurcation analysis of the bursting in the first part; (b) One-parameter bifurcation analysis of the bursting in the second part; (c) Two-parameter bifurcation of the trajectory in the (
,
) plane for the mixed bursting; (d) Partial enlargement of (c)
图5. [IP3] = 0.97 μM时的动力学分析。(a) 前部的单参数分岔分析;(b) 后部的单参数分岔分析;(c) 混合簇放电的轨线在(
,
)平面的双参数分岔;(d) 双参数分岔图的局部放大
树突型混合簇放电的轨线在(
,
)平面的双参数分岔如图5(c)所示,图5(d)为图5(c)的局部放大图。在
跳起之前,全系统轨线仅在鞍结分岔曲线f和同宿轨分岔曲线homo之间跃迁一次,这表明前部仅存在一个短簇。
当[IP3]增加至1 μM时,树突型混合簇的放电模式发生变化,如图6(a)所示。此时,前部的短簇消失,并出现持续峰放电。然而,后部的放电模式保持不变,仍然是经由“fold/homoclinic”滞后环的“Hopf/homoclinic”型簇放电。将[IP3]继续增加至1.3 μM,前部的持续峰放电消失,放电模式由混合簇放电变为树突簇放电,如图6(b)所示。此时,该树突簇为“fold/homoclinic”滞后环的“Hopf/homoclinic”型簇放电。
通过观察当参数[IP3] = 1 μM时系统轨线在(
,
)平面的双参数分岔图及其局部放大图(图6(c),图6(d)),可以看到轨线围绕鞍结分岔曲线f进行振荡,这对应于前部的持续峰放电(图6(a))。而图6(c),图6(f)展示了当参数[IP3] = 1.3 μM时的双参数分岔图及其局部放大图,可以观察到随着
增加,轨迹不再围绕鞍结分岔曲线f振荡,而是直接穿过鞍结分岔曲线f和同宿轨分岔曲线homo。这说明放电模式由混合簇转变为树突簇。
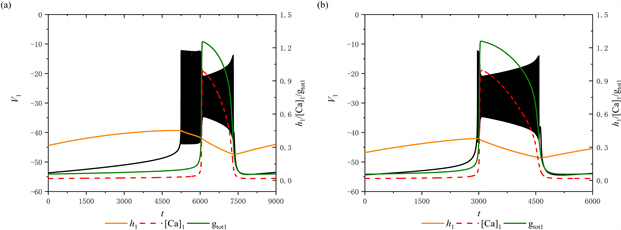

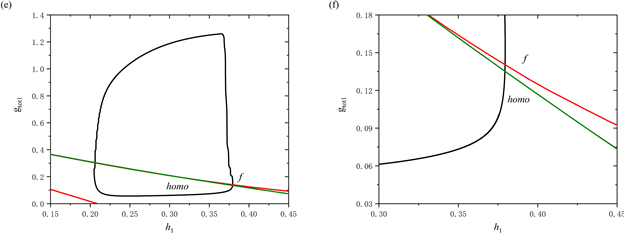
Figure 6. (a) The firing pattern of system with [IP3] = 1 μM; (b) The firing pattern of system with [IP3] = 1.3 μM; (c) Two-parameter bifurcation analysis with [IP3] = 1 μM; (d) Partial enlargement of (c); (e) Two-parameter bifurcation analysis with [IP3] = 1.3 μM; (f) Partial enlargement of (e)
图6. (a) [IP3] = 1 μM时放电模式;(b) [IP3] = 1.3 μM时放电模式;(c) 当[IP3] = 1 μM时的双参数分岔分析;(d) 双参数分岔图的局部放大;(e) 当[IP3] = 1.3 μM时的双参数分岔分析;(f) 双参数分岔图的局部放大
双参数分岔分析表明,如果全系统轨线在鞍结分岔曲线f和同宿轨分岔曲线homo之间来回跃迁,或者围绕鞍结分岔曲线f持续振荡时,会产生树突型混合簇放电。同时,全系统轨线在鞍结分岔曲线f和同宿轨分岔曲线homo之间跃迁的次数,与混合簇中前部短簇的数量相对应。
4. 总结
本文所探讨的是仅由树突子系统的钙振荡单独作用产生的一种特殊放电模式——树突型混合簇放电。之前研究 [22] 中发现了树突型混合簇放电现象,而本文则是进一步探究了耦合pre-Bötzinger复合体神经元模型中的树突型混合簇放电现象。根据文献 [22] 的思路,可以说明本文中所有的混合簇放电都是树突型混合簇放电。具体的证明细节不再详述。
在耦合pre-Bötzinger复合体神经元中,本文主要研究三磷酸肌醇浓度[IP3]对树突型混合簇放电的影响,并从动力学的角度揭示树突型混合簇放电模式的产生及其转迁机制。研究结果表明,随着[IP3]的增加,一个放电周期内短簇的数量逐渐减少。树突型混合簇放电的前部由多个相同的“fold/homoclinic”型簇放电变为单个“fold/homoclinic”型簇放电,后部的放电模式保持经由“fold/homoclinic”滞后环的“Hopf/homoclinic”型簇放电不变。另一方面,放电周期和持续时间都随着[IP3]的增加而减少,最终混合簇放电消失,放电模式由树突型混合簇放电转迁为树突簇放电。此外,通过双参数分岔分析,揭示了树突型混合簇放电的产生机制。如果轨线能够在鞍结分岔曲线和同宿轨分岔曲线之间来回跃迁,或者在鞍结分岔曲线周围持续振荡,那么全系统会呈现出树突型混合簇放电。树突型混合簇放电具有多样的动力学行为,进一步研究其产生和调控机制有助于全面了解神经元放电的动力学特性。
附录

Table A1. Parameter values in the theoretical model
表A1. 理论模型中的参数值