DOI:10.12677/PM.2023.1312385,PDF,HTML,XML,被引量下载: 304浏览: 409
作者:王雅卿^*,张思汇^#：上海理工大学理学院，上海
关键词:动力系统；回复时间集；F?lner序列；Dynamical System；Recurrent Set；F?lner Sequence

文章引用：王雅卿, 张思汇. 动力系统中n重回复时间集的性质研究[J]. 理论数学, 2023, 13(12): 3730-3735. https://doi.org/10.12677/PM.2023.1312385

1. 引言

我们首先引进回复时间点集的概念。

定义1.1 [1] ：对于一个动力系统 $\left(X,T\right)$，设 $x\in X$及 $U\subset X$，令x进入U的回复时间集为：

$N\left(x,U\right)=\left\{n\in {\mathbb{Z}}_{+}:T^{n}x\in U\right\}$.

显然，如果x为回复点，那么它也是 $T^n\left(n\in \mathbb{N}\right)$的回复点。

2016年，Kwietniak [2] 等人在探索由van der Waerden定理和类似的组合问题的动态方法所产生的递归性质时，证明了：

定理1.2 设 $\left(X,T\right)$是一个动力系统，如果在X上存在一个弱混合的、完全T-不变的Borel概率度量 $\mu$，则存在一个X的Borel子集 $X_0$，且 $\mu \left(x_0\right)=1$，使得对于任意 $x\in x_0$， $d\in \mathbb{N}$，以及X的每个非空开子集U，集合

$N_{T\times T^2\times \cdots \times T^d}\left(\left(x,x,\cdots ,x\right),U\times U\times \cdots \times U\right)$

具有正上密度。

2020年，陈志景，黄煜 [3] 等人研究了具有正上 $\left\{F_n\right\}$-密度的回复点，证明了所有正上 $\mathcal{F}$-密度的回复点的集合是Borel的，并且对于任意的 $\mu \in M\left(X,G\right)$，具有满的 $\mu$-测度。

如果对于x的每一个开邻域U，存在 $d\in \mathbb{N}$，使集合 $N_{T\times T^2\times \cdots \times T^d}\left(\left(x,\cdots ,x\right),U\times \cdots \times U\right)$具有上正的 $\mathcal{F}$-密度，则称点 $x\in X$具有多重回复的上正 $\mathcal{F}$-密度。

基于上述研究，我们提出下述问题：

问题1 设 $\left(X,T\right)$是一个G-系统， $\mu$是X上的一个弱混合的、完全T-不变的Borel概率度量，则存在一个X的Borel子集 $X_0$，且 $\mu \left(x_0\right)=1$，使得对于任意 $x\in x_0$， $d\in \mathbb{N}$，以及X的每个非空开子集 $U_1,U_2,\cdots ,U_d$，集合

$N_{T\times T^2\times \cdots \times T^d}\left(\left(x,x,\cdots ,x\right),U_1\times U_2\times \cdots \times U_d\right)$

具有正上 $\mathcal{F}$-密度。

2. 定义与符号

下面介绍一些基本的符号和定义。

2.1. G-系统

G-系统 $\left(X,G\right)$意味着X是紧致度量空间，G是可数离散无限可服从群， $\Gamma :G\times X\to X$， $\left(g,x\right)\to gx$是满足以下条件的连续映射：

$\Gamma \left(e,x\right)=x$，对任意的 $x\in X$，其中e是G的单位元。

$\Gamma \left(g_1,\Gamma \left(g_2\right)\right)=\Gamma \left(g_1{g}_2,x\right)$，对任意的 $g_1,g_2\in G$， $x\in X$

设 $\left(X,G\right)$是一个G-系统，且 $x\in X$，对于子集 $F\subset G$，用F-orbit表示X的轨道：

$Fx:=\left\{gx:g\in F\right\}$.

设 $U\subset X$，定义x的回复时间集为

$N\left(x,U\right):=\left\{g\in G:gx\in U\right\}$.

如果对于x的任意开邻域U，集合 $N\left(x,U\right)$是无穷的，则点 $x\in X$称为回复点。如果对于y的每一个开邻域U， $N\left(x,U\right)$是无穷的，则点 $y\in X$称为x的 $\omega$极限点。X的所有 $\omega$极限点的集合称为X的 $\omega$-极限集，用 ${\omega }_G(x)$表示。如果存在一个点 $y\in X$，使得y的 $\omega$-极限集在X中是稠密的，则称系统 $\left(X,G\right)$为可传递的，这样的点称为可传递点。

设 $\left(G,\cdot \right)$是紧致度量空间 $\left(X,G\right)$上的可数离散无限可服从群， $\left(X,G\right)$是紧度量空间 $\left(X,d\right)$上的拓扑动力系统(简称G-系统)。对于任意点 $x\in X$，我们称 $Gx=\left\{gx:g\in G\right\}$为x在G作用下的轨道。如果 $gx\in \Lambda$，对任意 $x\in \Lambda$和 $g\in G$，我们将X的任意子集 $\Lambda$称为G-不变集。在动力系统理论中，我们经常需要处理轨道Gx在X的给定区域E停留的概率。这促使我们考虑 $\left(X,G\right)$中的各种密度。

2.2. Fϕlner序列

G的一个有限子集的序列 $\mathcal{F}={\left\{F_n\right\}}_{n=1}^{\infty }$被称为G中的(左) Fϕlner序列，如果

$\underset{n\to \infty }{\lim }\frac{\left|g{F}_n\Delta F_n\right|}{\left|F_n\right|}=0$， $\forall g\in G$，

其中 $|·|$是G上的计数测度。显然，Fϕlner序列的每个子序列 ${\left\{F_{n_k}\right\}}_{k=1}^{\infty }$也是G中的Fϕlner序列。众所周知，只要G是可服从的，就会存在Fϕlner序列 [4] 。

对于给定的Fϕlner序列 $\mathcal{F}:={\left\{F_n\right\}}_{n=1}^{\infty }$，在G和一个子集 $A\subseteq G$中，A相对于 $\mathcal{F}$的上、下密度分别由

${\bar{d}}_{\mathcal{F}}\left(A\right)=\underset{n\to \infty }{\lim \sup }\frac{\left|A\cap F_n\right|}{\left|F_n\right|}$和 ${\underset{\_}{d}}_{\mathcal{F}}\left(A\right)=\underset{n\to \infty }{\lim \inf }\frac{\left|A\cap F_n\right|}{\left|F_n\right|}$

定义。

如果 ${\bar{d}}_{\mathcal{F}}\left(A\right)={\underset{\_}{d}}_{\mathcal{F}}\left(A\right)$，那么我们称这个值为A相对于 $\mathcal{F}$的密度。

现在，对于一个子集 $E\subseteq X$和一个Fϕlner序列 $\mathcal{F}={\left\{F_n\right\}}_{n=1}^{\infty }$，轨道Gx在 $E\left(X\right)$中停留的概率可以用以下量来描述：

${\bar{d}}_{\mathcal{F}}\left(A\right)=\left(\left\{g\in G:gx\in E\right\}\right)$

${\underset{\_}{d}}_{\mathcal{F}}\left(A\right)=\left(\left\{g\in G:gx\in E\right\}\right)$

或者

$d_{\mathcal{F}}\left(A\right)=\left(\left\{g\in G:gx\in E\right\}\right)$

当 $d_{\mathcal{F}}$-密度存在时。这促使我们考虑G-系统的以下概念： $ℝ$-actions [5] 、 ${ℝ}_{+}$-actions [6] 和 $C^0$-semiflow [7] 。

定义2.1 对于Fϕlner序列 $\mathcal{F}={\left\{F_n\right\}}_{n=1}^{\infty }$，对于x的每一个开邻域

U， ${\bar{d}}_{\mathcal{F}}\left(A\right)=\left(\left\{g\in G:gx\in U\right\}\right)>0$，点 $x\in X$是循环的且上 $\mathcal{F}$-密度为正；如果对于x的每一个开邻域U， ${\underset{\_}{d}}_{\mathcal{F}}\left(A\right)=\left(\left\{g\in G:gx\in U\right\}\right)>0$，点 $x\in X$是循环的且下 $\mathcal{F}$-密度为正。

根据G-系统的逐点遍历定理 [8] ，不难看出，在遍历理论中存在“许多”点，其上 $\mathcal{F}$密度为正，其中Fϕlner序列 $\mathcal{F}={\left\{F_n\right\}}_{n=1}^{\infty }$满足Shulman’s条件 [8] ：

$\left|{\displaystyle \underset{k<n}{\cup }{F}_k{}^{-1}{F}_n}\right|\le C\left|F_n\right|$，对某些 $C>0$以及任意 $n\in \mathbb{N}$。

我们利用平均遍历定理证明了这一性质对任何不存在Shulman’s条件的Fϕlner序列都成立，并描述了具有正上 $\mathcal{F}$-密度的循环点集合的拓扑“大小”如下：

定理2.1 所有上 $\mathcal{F}$密度为正的循环点的集合是Borel的，并且对于任意的 $\mu \in \mathcal{M}\left(X,G\right)$具有满 $\mu$测度。

在一定的合理条件下，从拓扑学的角度来看，上 $\mathcal{F}$-密度为正的循环点集很大。

定理2.2 如果存在一个完全支持的遍历G-不变测度 $\left(X,G\right)$，则所有上 $\mathcal{F}$-密度为正的循环点的集合为残差。

定理2.3 (G-系统的sigmund猜想)设 $\left\{F_n\right\}$是G的一个双边Fϕlner序列。如果存在一个 $x\in X$，满足性质( $\ast$) ${\bar{d}}_{\mathcal{F}}=\left(\left\{g\in G:gx\in U\right\}\right)>0$，对于任意 $y\in X$和y的开邻域U，则所有具有性质( $\ast$)的点的集合在X上是残差。

定义2.4 对于G中的 $x\in X$和Fϕlner序列 $\mathcal{F}={\left\{F_n\right\}}_{n=1}^{\infty }$，如果对任意 $\epsilon >0$，有 $d_{\mathcal{F}}\left(\left\{g\in G:gx\in B\left(C,\epsilon \right)\right\}\right)=1$，则X的闭子集C称为x的 $\mathcal{F}$-吸引中心。如果集合C不存在任何固有子集，它同样是x的 $\mathcal{F}$-吸引中心，则C称为x的最小 $\mathcal{F}$-吸引中心，并写为 ${\mathcal{C}}_{\mathcal{F}}\left(x\right)$。这里 $B\left(C,\epsilon \right)$表示X中C周围的 $\epsilon$-邻域。

最近几年关于动力系统的研究，主要参考文献 [1] [6] [9] [10] [11] [12] [13] 。

3. 定理与证明

定理3：设 $\left(X,G\right)$是一个拓扑动力系统，对任意，存在一个 $\mu \left(X_0\right)=1$的Borel子集 $X_0$，使得对任意 $x\in X$， $d\in \mathbb{N}$以及x的任意邻域U，集合

$N_{T\times T^2\times \cdots \times T^d}\left(\left(x,x,\cdots ,x\right),U_1\times U_2\times \cdots \times U_d\right)$

具有正上 $\mathcal{F}$-密度。

证明：对任意 $t>0$， $d,k,n,m\in \mathbb{N}$，设 $A_{d,k}\left(t,n,m\right)$为所有点 $x\in X$的集合，使得存在一个x的开邻域U，且 $diam\left(U\right)<\frac{1}{k}$，满足

$\frac{\left|F_n\cap N_{T\times T^2\times \cdots \times T^d}\left(\left(x,\cdots ,x\right),U\times \cdots \times U\right)\right|}{\left|F_n\right|}>t-\frac{1}{m}$.

对任意 $k\in \mathbb{N}$，设

$A_{d,k}\left(t,n,m\right)={\displaystyle \underset{i=1}{\overset{\infty }{\cup }}{\displaystyle \underset{m=1}{\overset{\infty }{\cap }}{\displaystyle \underset{n=m}{\overset{\infty }{\cup }}{A}_{d,k}\left(\frac{1}{i},n,m\right)}}}$

则在交点 $X_0$上具有正 $\mathcal{F}$-密度的多回复点的集合，因此它是Borel集合，因为每个 $A_k\left(t,n,m\right)$都是X的开子集。

通过遍历分解定理，我们只需要证明遍历测度的结果成立。设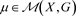，我们假定每个 $A_{d,k}$都有满 $\mu$测度。相反，假设对于某些 $k\in \mathbb{N}$， $A_{d,k}<1$，则我们可以选择一个 $diam\left(D\right)<\frac{1}{3k}$且 $\mu \left(D\right)>0$Borel子集 $D\subset X\backslash A_k$。对于任意 $x\in X$，令

$\phi \left(x\right)=\underset{n\to \infty }{\lim \sup }\frac{1}{\left|F_n\right|}{\displaystyle \underset{g\in F_n}{\sum }{1}_{D\cap G^{-i}\cap \cdots \cap G^{-id}D}\left(x\right)}$，

则对于任意 $x\in X$， $\varphi$也是Borel可测的，且 $0\le \varphi \left(x\right)\le 1$。

利用平均遍历定理，得到 ${\left\{F_n\right\}}_{n=1}^{\infty }$的一个子序列 ${\left\{F_{n_k}\right\}}_{k=1}^{\infty }$，使得

$\frac{1}{\left|F_{n_k}\right|}{\displaystyle \underset{g\in F_{n_k}}{\sum }{1}_{D\cap G^{-i}\cap \cdots \cap G^{-id}D}\left(x\right)}\to \mu \left(x\right)$，

在 $L^2$-norm $\Vert •\Vert$， $L^2\left(X.\mathcal{B}\left(X\right),\mu \right)$， $k\to \infty$。因此，根据法图引理，有

$\begin{array}{c}{\displaystyle {\int }_D\phi \left(x\right)\text{d}\mu \left(x\right)}\ge \underset{n\to \infty }{\lim \sup }{\displaystyle {\int }_D\frac{1}{\left|F_n\right|}{\displaystyle \underset{g\in F_n}{\sum }{1}_{D\cap G^{-i}D\cap \cdots \cap G^{-id}D}\left(x\right)\text{d}\mu \left(x\right)}}\\ =\underset{n\to \infty }{\lim \sup }\langle \frac{1}{\left|F_n\right|}{\displaystyle \underset{g\in F_n}{\sum }{1}_{D\cap G^{-i}\cap \cdots \cap G^{-id}D}\left(x\right)},1_D\rangle \\ \ge \underset{n\to \infty }{\lim }\langle \frac{1}{\left|F_n\right|}{\displaystyle \underset{g\in F_n}{\sum }{1}_{D\cap G^{-i}\cap \cdots \cap G^{-id}D}\left(x\right)},1_D\rangle \\ =\mu {\left(D\right)}^2>0\end{array}$

显然，对于任意 $X\notin B$， $\phi \left(x\right)=0$，因此存在某个 $x\in B$，使得 $\phi \left(x\right)>0$。令

$U=B\left(x,\frac{2}{3k}\right):=\left\{y\in X:d\left(x,y\right)<\frac{2}{3k}\right\}$，

则 $D\subset U$， $N_{T\times T^2\times \cdots \times T^d}\left(\left(x,\cdots ,x\right),U\times \cdots \times U\right)$的上 $\mathcal{F}$-密度不小于 $\phi \left(x\right)$。

我们得到 $x\in A_{d,k}$，矛盾！

因此对于每一个遍历测度 $\mu$， $d,k\in \mathbb{N}$， $\mu \left(A_{d,k}\right)=1$。令

$X_0={\displaystyle \underset{d=1}{\overset{\infty }{\cap }}{\displaystyle \underset{k=1}{\overset{\infty }{\cap }}{A}_{d,k}}}$

则对于每一个遍历测度 $\mu \left(X_0\right)=1$，通过遍历分解同样成立。

因此 $X_0$是需要的。

NOTES

^*第一作者。

^#通讯作者。

参考文献

[1]	Einsiedler, M. and Ward, T. (2010) Ergodic Theory: With a View towards Number Theory. Graduate Texts in Mathe-matics, Vol. 259, Springer-Verlag, New York. https://doi.org/10.1007/978-0-85729-021-2
[2]	Dominik, K., Li, J., Oprocha, P. and Ye, X. (2016) Multi-Recurrenve and van der Waerden System. Science China (Mathematics), 60, 59-82.
[3]	Chen, Z., Huang, Y. and Liu, X. (2020) Recurrence and the Minimal Center of Attraction with Respect to a Følner Sequence. Topology and Its Applications, 275, Article 107156. https://doi.org/10.1016/j.topol.2020.107156
[4]	Greschonig, G. and Schmidt, K. (2000) Ergodic Decomposition of Quasi-Invariant Probability Measures. Colloquium Mathematicum, 84, 495-514. https://doi.org/10.4064/cm-84/85-2-495-514
[5]	Huang, Y. and Zhou, Z. (2012) Two New Recurrent Levels for C0-Flows. Acta Applicandae Mathematicae, 118, 125-145. https://doi.org/10.1007/s10440-012-9681-7
[6]	Dai, X. (2016) On Chaotic Minimal Center of Attraction of a Lagrange Stable Motion for Topological Semi Flows. Journal of Differential Equations, 260, 4393-4409. https://doi.org/10.1016/j.jde.2015.11.019
[7]	del Junco, A. and Ros-enblatt, J. (1979) Counterexamples in Ergodic Theory and Number Theory. Mathematische Annalen, 245, 185-197. https://doi.org/10.1007/BF01673506
[8]	Sigmund, K. (1977) On Minimal Centers of Attraction and Generic Points. Journal für die reine und angewandte Mathematik, 295, 72-79. https://doi.org/10.1515/crll.1977.295.72
[9]	Hilmy, H.F. (1936) Sur les centres d’attraction minimaux des systèmes dynamiques. Compositio Mathematica, 3, 227-238.
[10]	Lindenstrauss, E. (2001) Pointwise Theorems for Amenable Groups. Inventiones Mathematicae, 146, 259-295. https://doi.org/10.1007/s002220100162
[11]	Hindman, N. and Strauss, D. (2006) Density in Arbitrary Semigroups. Semigroup Forum, 73, 273-300. https://doi.org/10.1007/s00233-006-0622-5
[12]	Tian, X. (2016) Different Asymptotic Behaviour versus Same Dynamical Complexity: Recurrence and Regularity. Advances in Mathematics, 288, 464-526. https://doi.org/10.1016/j.aim.2015.11.006
[13]	Chen, Z. and Dai, X. (2017) Chaotic Dynamics of Minimal Center of Attraction of Discrete Amenable Group Actions. Journal of Mathematical Analysis and Applications, 456, 1397-1414. https://doi.org/10.1016/j.jmaa.2017.07.053